Експеримент Кавендіша
| Експеримент Кавендіша | |
 | |
| Названо на честь | Генрі Кавендіш[1] |
|---|---|
| Час/дата початку | 1797 |
| Час/дата закінчення | 1798 |
 | |
| | |
Експериме́нт Каве́ндіша — перший експеримент, у якому була виміряна сила гравітації між масами в лабораторних умовах, а також, перша методика, яка дозволила визначити точне значення гравітаційної сталої, проведений у 1797–1798 роках англійським вченим Генрі Кавендішем[2]. З врахуванням систем мір того часу, гравітаційна стала не була вказана явно у працях Кавендіша. Замість неї було визначено середню густину Землі, що рівнозначне до визначення маси Землі. Це було перше точне обчислення цих геофізичних сталих. Для проведення експерименту Кавендіш використав результати попередніх робіт з 1783 року[3] його земляка, геолога Джона Мічелла[4], що створив обладнання під назвою «крутильні терези». Дж. Мічелл помер у 1793 році і не завершив своїх досліджень, а його обладнання перейшло до Френсіса Джона Гайд Волластона (англ. Francis John Hyde Wollaston), а потім до Генрі Кавендіша, який переробив дещо прилад, не порушуючи оригінального задуму Мічелла. Далі Кавендіш провів на обладнанні серію вимірювань, а результати опублікував у Philosophical Transactions of the Royal Society у 1798 році[5].
Експеримент[ред. | ред. код]


Крутильні терези виконані на базі дерев'яного стрижня (коромисла) довжиною 6 футів (1,8 м) підвішеного на дроті довжиною близько 1 м з міді, покритого сріблом, на кінцях якого були закріплені свинцеві кулі діаметром 3 дюйми (51 мм) і масою 1,61 фунти (0,73 кг). Дві 12-дюймові (300 мм) свинцеві кулі масою 348 фунтів (158 кг) розташовані поблизу менших куль на відстані близько 9 дюймів (230 мм), закріплені на незалежній підвісці[6]. В експерименті вимірювалась сила взаємодії між малою і великою кулями.
Дві більші кулі розташовувались на протилежних сторонах горизонтального дерев'яного коромисла терезів. Взаємне притягання до менших куль спричиняло повертання коромисла приводячи до скручування дроту на якому воно підвішене. Коромисло поверталось на кут, при якому сила скручення дроту зрівноважувала гравітаційну силу притягання між кулями. Знаючи кут повороту і момент сили скручування у залежності від кута, Кавендіш зміг визначити силу взаємодії пари мас. Оскільки гравітаційна сила, з якою Земля діє на меншу кулю може бути виміряна безпосередньо шляхом її зважування, із співвідношення двох сил можна визначити густину Землі на основі закону всесвітнього тяжіння.
Кавендіш обчислив, що густина Землі у 5,448 ± 0,033 разів більша від густини води (через просту помилку при обчисленнях, яку зауважив Френсіс Бейлі, помилкове значення, що приводиться у документах, становило 5,48 ± 0,038)[7].
Для того щоб обчислити величину крутного моменту, прикладеного до дроту для даного кута повороту, Кавендіш обчислив жорсткість при крученні через визначення періоду власних коливань крутильного маятника, виведеного із стану рівноваги. Період коливань становив близько 20 хвилин. Знаючи розмір і кут повертання коромисла можна обчислити значення крутного моменту. Насправді коромисло ніколи не було у стані спокою. Кавендіш змушений був вимірювати кут відхилення в умовах коливань[8].
Як на ті часи, обладнання Кавендіша характеризувалось досить високою чутливістю[7]. Сила від скручування, приведена до плеча коромисла була надзвичайно малою, 1,74 × 10−7 Н[9], близько 1/50000000 від ваги меншої кулі[10] або відповідала вазі піщинки[11].
Щоб зменшити похибки вимірювань спричинені повітряними потоками і зміною температури, Кавендіш помістив апаратуру у дерев'яний корпус з товщиною стінки 3 фути (0,61 м), висотою 10 футів (3 м) i шириною 10 футів (3 м), розташованому у закритому приміщенні. Спостереження коливань Кавендіш проводив через два отвори у стінах приміщення за допомогою телескопа. Коливання коромисла становили менше 0,16 дюйма (4,1 мм)[12]. Кавендіш зміг виміряти такі малі відхилення з точністю до 0,01 дюйма завдяки ноніусу на кінці плеча[13].
Reich (1838), Baily (1843), Cornu & Baille (1878) та багато інших дослідників повторювали експеримент Кавендіша. Точність експерименту не могли покращити упродовж 97 років, зробив це Чарлз Вернон Бойз у 1895 році. У цей період крутильні терези Мічелла були основним обладнанням для вимірювання гравітаційної сталої (G) і більшість сучасних методик є лише їх модифікаціями. З огляду на це описана методика дослідження отримала назву експеримент Кавендіша[14].
Чи Кавендіш визначив гравітаційну сталу G?[ред. | ред. код]
Отримані результати Кавендіш подавав як визначення густини Землі, а свій експеримент у листуванні називав «зважуванням світу». Минуло багато років, перш ніж Закон всесвітнього тяжіння, у формулюванні якого застосовується гравітаційна стала, став загальноприйнятим. Одна з перших згадок про гравітаційну сталу належить до 1873 року (через 75 років після публікацій Кавендіша)[15].
З цієї причини історики науки твердять, що Кавендіш не вимірював гравітаційної сталої[16][17][18][19].
Втім, наступні автори уже інтерпретували його результати у сучасній формі[20][21][22] де:
Після переходу на одиниці SI і підстановкою густини Землі отриманої Кавендішом 5,448 г см−3 можна обчислити
- G = 6,74 × 10−11 м³ кг−1 с−2,
що лише на 1% відрізняється від сучасного загальноприйнятого значення: 6,67384 × 10−11 м³ кг−1 с−2 [23].
Тому часто Кавендішу приписують заслугу першості у визначенні гравітаційної сталої[24][25][26][27][28].
Фізики часто використовують вирази, у яких гравітаційна стала має інший вигляд. Серед астрономічних констант має застосування гравітаційна стала Гауса (k), запропонована Гаусом у праці Theoria motus corporum coelestium in sectionibus conicis solem ambientum («Теорія руху небесних тіл, які обертаються навколо Сонця по конічних кривих») від 1809 року, а експеримент Кавендіша можна розглядати як метод визначення астрономічної одиниці. У часи Кавендіша фізики використовували однакові одиниці для маси і сили тяжіння. Далі, беручи як стандартне прискорення а було відоме, виконувала роль величини, оберненої до гравітаційної сталої. Через це густина Землі була величиною, пошук значення якої був досить інтенсивним у ті часи, що підтверджують також інші спроби дослідників (наприклад, Шихаліонський експеримент англ. Schiehallion experiment у 1774 році).
Визначення G і маси Землі[ред. | ред. код]
- Опис умовних позначень подано у таблиці в кінці розділу.
Подана методика не відбиває методику, якою користувався Кавендіш, але показує як сучасні фізики можуть скористатись його результатами[29][30][31]. Відповідно до закону Гука, момент сили є пропорційним до кута повороту коромисла .
де константа , що носить назву «жорсткість при крученні» і залежить від параметрів підвісу (виду матеріалу, довжини і діаметра дроту). Крім цього момент сили може бути записаний як добуток сили взаємного протягування куль і відстані точки підвісу від осі обертання. Оскільки є дві пари куль і кожна взаємодіє із силою F на відстані L/2 від осі, повний момент буде становити LF. Прирівнюючи обидва рівняння, можна записати:
Сила F згідно із законом всесвітнього тяжіння І.Ньютона:
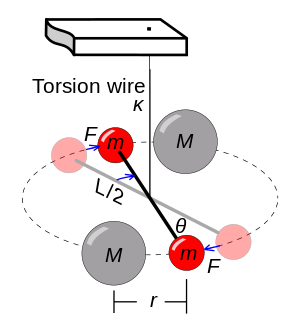
Підставляючи її до першого рівняння отримуємо
З метою визначення жорсткості підвісу при крученні (), Кавендіш виміряв період вільних коливань T системи:
що дає
Знаходячи з нього , після підстановки в (1) і визначення G можна отримати:
Знаючи G, можна використати силу земного тяжіння для обчислення маси і густини Землі:
| Визначення позначень | ||
| Відхилення коромисла від стану рівноваги | ||
| Сила гравітації між масами M і m | ||
| Гравітаційна стала | ||
| Маса меншої свинцевої кулі | ||
| Маса більшої свинцевої кулі | ||
| Відстань між центрами куль меншої і більшої коли терези мають відхил від стану рівноваги | ||
| Довжина коромисла, відстань між центрами менших куль | ||
| Жорсткість при крученні дроту підвісу коромисла | ||
| Крутний момент коромисла терезів | ||
| Період коливань торсіонного маятника | ||
| Прискорення вільного падіння на поверхні Землі | ||
| Маса Землі | ||
| Радіус Землі | ||
| Густина Землі | ||
Див. також[ред. | ред. код]
Примітки[ред. | ред. код]
- ↑ Berry A. A Short History of Astronomy — London: John Murray, 1898.
- ↑ Boys 1894 [Архівовано 11 липня 2019 у Wayback Machine.] s.355
- ↑ McCormmach & Jungnickel 1996 [Архівовано 1 січня 2014 у Wayback Machine.], s.336: У листі від 1783 Каведіша до Джона Мічелла можна прочитати «…колишня згадка про зважування світу». Не зрозуміло чи «колишня згадка» стосується Кавендіша чи Мічелла.
- ↑ Cavendish 1798 [Архівовано 10 липня 2019 у Wayback Machine.], s.59 Кавендіш віддає Мічеллу усі заслуги у розробці експерименту
- ↑ Cavendish H. Experiments to determine the Density of the Earth, Philosophical Transactions of the Royal Society of London, (part II) 88 s.469-526 (21 June 1798), перевидано Cavendish 1798 [Архівовано 10 липня 2019 у Wayback Machine.]
- ↑ Cavendish 1798 [Архівовано 10 липня 2019 у Wayback Machine.], s.59
- ↑ а б Poynting 1894 [Архівовано 6 травня 2016 у Wayback Machine.], s.45
- ↑ Cavendish 1798 [Архівовано 28 червня 2014 у Wayback Machine.], s.64
- ↑ Boys 1894 [Архівовано 12 січня 2014 у Wayback Machine.] P.357
- ↑ Cavendish 1798 [Архівовано 17 січня 2013 у Wayback Machine.] P.60
- ↑ Піщинка з грануляцією 2 мм має вагу ~13 мГс. Theodoris Marina Mass of a Grain of Sand [Архівовано 28 травня 2013 у Wayback Machine.]. The Physics Factbook. 2003 (англ.)
- ↑ Cavendish 1798 [Архівовано 12 січня 2014 у Wayback Machine.], P.99, Таблиця результатів, (поділка шкали = 1/20" ≈ 1,3 мм). Повне відхилення при дослідженнях було у двічі більшим, однак це відхилення спричинялось двома кулями на протилежних плечах коромисла терезів.
- ↑ Cavendish 1798 [Архівовано 12 січня 2014 у Wayback Machine.], P.63
- ↑ McCormmach & Jungnickel 1996 [Архівовано 7 липня 2014 у Wayback Machine.], P.341
- ↑ Cornu A., Baille, J. B. Mutual determination of the constant of attraction and the mean density of the earth. C. R. Acad. Sci., Paris, 1873.- Vol. 76, P. 954–958.
- ↑ Clotfelter 1987
- ↑ McCormmach & Jungnickel 1996 [Архівовано 1 січня 2014 у Wayback Machine.], P.337
- ↑ Hodges 1999. Архів оригіналу за 6 вересня 2017. Процитовано 3 лютого 2013.
- ↑ Lally 1999
- ↑ Boys 1894 [Архівовано 12 листопада 2012 у Wayback Machine.], P.330 У цій доповіді, Бойз (Boys) вводить сталу G і аргументує її використання
- ↑ Poynting 1894 [Архівовано 5 липня 2014 у Wayback Machine.], P.4
- ↑ MacKenzie 1900 [Архівовано 12 листопада 2012 у Wayback Machine.], P.VI
- ↑ Newtonian constant of gravitation. Архів оригіналу за 26 червня 2021. Процитовано 19 березня 2022.
- ↑ David Halliday, Robert Resnick Fundamentals of Physics. John Wiley & Sons, 1993, p. 418. ISBN 9780471147312. (англ.) «Обладнання з 1798 року завдяки якому Генрі Кавендіш виміряв гравітаційну сталу»
- ↑ Richard P. Feynman Lectures on Physics, Vol.1. , P. 6-7, 1963. Addison-Wesley (англ.). «Кавендіш стверджував, що зважив Землю, хоча він насправді виміряв коефіцієнт G…»
- ↑ Richard P. The Character of Physical Law. , P. 28, 1967. MIT Press (англ.). «Кавендіш отримав можливість виміряти силу, дві маси і відстань, а на основі цього описати гравітаційну сталу G»
- ↑ Cavendish Experiment, Harvard Lecture Demonstrations, Harvard Univ (англ.). «[крутильні терези були]…модернізовані Кавендішем для вимірювання G.»
- ↑ Jonathan Shectman Groundbreaking Experiments, Inventions, and Discoveries of the 18th Century. Greenwood, 2003, s. xlvii. ISBN 9780313320156. (англ.). «Кавендіш обчислює гравітаційну сталу, що дало можливість визначити масу Землі...»
- ↑ Експеримент Кавендіша, демонстраційні викладки, Гарварський університет. Архів оригіналу за 17 лютого 2011. Процитовано 3 лютого 2013.
- ↑ Poynting 1894 [Архівовано 5 січня 2014 у Wayback Machine.], P.41
- ↑ Clotfelter 1987 P.212 описує оригінальну методику обчислень Кавендіша
Джерела[ред. | ред. код]
- Boys C. Vernon. On the Newtonian constant of gravitation. / «Nature». 50 (1292), С. 330–334, 1894. doi:10.1038/050330a0. Bibcode: 1894Natur..50..330. (англ.).
- Cavendish Henry (1798). Experiments to Determine the Density of the Earth. In MacKenzie, A. S. Scientific Memoirs Vol.9: The Laws of Gravitation. American Book Co. 1900. C. 59-105 Копія оригінальних праць Кавендіша з 1798 року, та інші ранні дослідження, що стосуються визначення гравітаційної сталої.
- B. E. Clotfelter The Cavendish experiment as Cavendish knew it. / American Journal of Physics. 1987, 55 (3). С. 210–213. doi:10.1119/1.15214. Bibcode: 1987AmJPh..55..210C (англ.). Стверджується, що Кавендіш не визначив гравітаційної сталої.
- Falconer Isobel Henry Cavendish: the man and the measurement / Measurement Science and Technology 1999, 10 (6): С. 470–477. Bibcode 1999MeScT..10..470F. doi:10.1088/0957-0233/10/6/310 (англ.).
- «Gravitation Constant and Mean Density of the Earth» / Encyclopædia Britannica, 11th Ed.. 12. The Encyclopædia Britannica Co.. 1910. С. 385–389. (англ.).
- Hodges Laurent The Michell-Cavendish Experiment, [Архівовано 6 вересня 2017 у Wayback Machine.] Department of Physics and Astronomy, Iowa State University, Ames, IA. 1998. (англ.).
- Sean P. Lally Henry Cavendish and the Density of the Earth. / The Physics Teacher. 37 (1), С. 34-37, 1999. doi:10.1119/1.880145. Bibcode: 1999PhTea..37…34L (англ.).
- Russell McCormmach, Christa Jungnickel Cavendish. — Philadelphia, Pennsylvania: American Philosophical Society, 1996. — 414 c. ISBN 0-87169-220-1. (англ.).
- John H. Poynting The Mean Density of the Earth [Архівовано 13 березня 2016 у Wayback Machine.] . — London: C. Griffin & Co., 1894. — 156 с (англ.).







































