Корінь (математика)
Це стаття про добування коренів. Див. також Корінь функції та Радикал цілого числа.

Корінь -го степеня із числа визначається[1] як таке число , що Тут — натуральне число, що зветься показником кореня (або степенем кореня); як правило, воно більше або дорівнює 2, тому що випадок є тривіальним (звичайним). Добування кореня є протилежною математичною операцією до операції піднесення числа в степінь.
Позначення: символ (знак кореня) в правій частині називається радикалом. Число (підкореневий вираз) найчастіше дійсне або комплексне.
Приклади для дійсних чисел:
- тому що
- тому що
- тому що
Як видно з першого прикладу, у дійсного кореня можуть бути два значення (додатнє і від'ємне), і це ускладнює роботу з коренем. Щоб забезпечити однозначність, вводиться поняття арифметичного кореня, значення якого завжди невід'ємне, в першому прикладі це число
Означення та пов'язані поняття[ред. | ред. код]
Крім наведеного вище, можна дати два рівносильних означення кореня[2]:
- Коренем -го степеня із числа є розв'язок рівняння (відзначимо, що розв'язків може бути кілька або жодного);
- Коренем -го степеня із числа є корінь многочлена тобто значення , при якому зазначений многочлен дорівнює нулю.

Операція обчислення називається «добуванням кореня -го степеня» із числа . Це одна з двох операцій, обернених піднесенню до степеня,[3] а саме — знаходження основи степеня за відомим показником і результатом піднесення до степеня . Друга обернена операція, логарифмування, знаходить показник степеня за відомою основою та результатом.
Корені другого і третього степеня використовуються особливо часто і тому мають спеціальні назви.[3]
- Квадратний корінь: У цьому випадку показник степеня 2 зазвичай опускається, а термін «корінь» без вказівки степеня найчастіше позначає квадратний корінь. Геометрично можна розглядати як довжину сторони квадрата, площа якого дорівнює .
- Кубічний корінь: Геометрично — це довжина ребра куба, об'єм якого дорівнює .
Корені з дійсних чисел[ред. | ред. код]
Корінь -го степеня із дійсного числа , в залежності від парності і знака , може мати від 0 до 2 дійсних значень.
Загальні властивості[ред. | ред. код]
- Корінь непарного степеня із додатного числа — додатне число, однозначно визначене.
| , де — непарне |
- Наприклад,
- Корінь непарного степеня із від'ємного числа — від'ємне число, однозначно визначене.
| , де — непарне |
- Наприклад,
- Корінь парного степеня із додатного числа має два значення з протилежними знаками, але рівні за модулем.
| , де — парне |
- Наприклад,
- Корінь парного степеня із від'ємного числа не існує у області дійсних чисел, оскільки при піднесенні будь-якого дійсного числа до степеня з парним показником результатом буде невід'ємне число. Нижче буде показано, як знаходити такі корені в ширшій системі — множині комплексних чисел (тоді значеннями кореня будуть комплексних чисел).
| не існує, якщо — парне |
- Корінь будь-якого натурального степеня від нуля — нуль.
| де |

Арифметичний корінь[ред. | ред. код]
Корені парного степеня визначені, взагалі кажучи, неоднозначно, і цей факт створює незручності при їх використанні. Тому було введено практично важливе обмеження цього поняття[4].
Арифметичний корінь -го степеня з невід'ємного дійсного числа — це таке невід'ємне число , що Позначається арифметичний корінь тим же знаком радикала.
Таким чином, арифметичний корінь, на відміну від раніше визначеного (алгебраїчного[5]), визначається лише для невід'ємних дійсних чисел, а його значення завжди існує, однозначно[6] і невід'ємне. Наприклад, квадратний корінь з числа має два значення: та , з них арифметичним є перше.
- Оскільки арифметичний корінь і алгебраїчний позначаються одним і тим же символом, але є різними об'єктами, в рамках даної статті арифметичний корінь позначається синім кольором, а алгебраїчний — чорним.
Алгебраїчні властивості[ред. | ред. код]
Наведені нижче формули вірні, перш за все, для арифметичних коренів будь-якого степеня, у яких знак радикала виділений синім кольором (крім особливо обумовлених випадків). Вони справедливі також для коренів непарного степеня, у яких допускаються і від'ємні підкореневі вирази[7].
- Взаємоскорочення кореня і степеня[8] — для непарного : , для парного :
- Якщо , то і
Корінь з добутку дорівнює добутку коренів із співмножників:
Аналогічно для ділення:
Наступна рівність є означенням піднесення у дробову степінь[9]:
Величина кореня не зміниться, якщо його показник і степінь підкореневого виразу розділити на їх спільний множник:
- Приклад:
Для коренів непарного степеня є додаткова властивість:
- непарне.
Добуток кореня та піднесення до степеня[ред. | ред. код]
Операція піднесення до степеня спочатку була введена як скорочений запис операції множення натуральних чисел: . Наступним кроком було визначення піднесення в довільну цілу, в тому числі від'ємну, степінь:
Операція здобування арифметичного кореня дозволяє визначити піднесення додатнього числа в будь-яку раціональну (дробову) степінь:[9]
При цьому чисельник дробу може мати знак. Властивості розширеної операції переважно аналогічні піднесенню до цілого степеня.
Це визначення означає, що витяг кореня та зворотне до нього зведення в степінь фактично об'єднуються в одну алгебраїчну операцію. Зокрема:
Спроби зведення в раціональну степінь негативних чисел можуть привести до помилок, оскільки значення алгебраїчного кореня неоднозначне, а область значень арифметичного кореня обмежена невід'ємними числами. Приклад можливої помилки:
Функція кореня[ред. | ред. код]
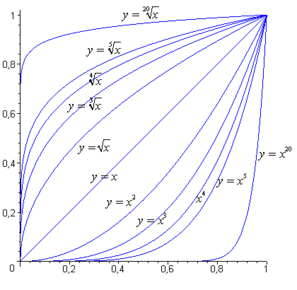
- Графіки функцій кореня
-
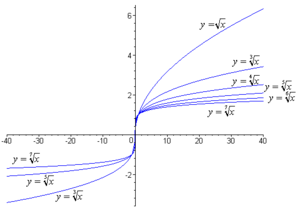
Функції кореня та зворотні до них статичні функції на інтервалі
-
функції кореня:
— арифметичний, парні степені 2, 4, 6
— загальний, непарні степені 3, 5, 7
Якщо розглядати підкорінний вираз як змінну, ми отримаємо функцію кореня -го степеня: .
Функція кореня належить до категорії алгебраїчних функцій.
Графік функції кореня будь-якого степеня проходить через початок координат та точку .
Як сказано раніше про корінь парного степеня, щоб забезпечити однозначність функції його, він повинен бути арифметичним, так що аргумент невід'ємний. Функція кореня непарного степеня однозначна та існує для будь-якого дійсного значення аргументу.
| Тип функції кореня | Область визначення | Область значень | Інші властивості |
|---|---|---|---|
| парні степені | Функція опукла вгору на всій області визначення | ||
| непарні степені | функція непарна |
Для будь-якого степеня функція кореня строго зростає, неперервна усюди всередині своєї області визначення. Необмежено диференційована усюди, крім початку координат, де похідна набуває значення нескінченності [10].
Похідна функції кореня визначається за формулою[11]:
- . Зокрема, .
Функція необмежено інтегрована на всій області визначення. Невизначений інтеграл можливо знаходити за формулою:
- .
- Зокрема, , де — довільна стала.
- Формула знаходження похідної -го порядку[[#cite_note-FOOTNOTEФіхтенгольц_Г._М._Курс_диференціального_й_інтегрального_числення1966Т._I,_С._233,_окремий_випадок_для_'"`UNIQ--math-00000073-QINU`"'.-12|[12]]] функції :
| де |
- Формула знаходження -го невизначеного інтеграла[13] функції :
| де |
- Праві частини формул є алгебраїчними виразами, які існують завжди, при натуральному . Отже і ліві теж.
Граничні співвідношення[ред. | ред. код]
Наведемо кілька корисних границь, що містять корені[14].
Практичне обчислення коренів[ред. | ред. код]
Функція обчислення квадратних та кубічних коренів передбачена в багатьох калькуляторах; наприклад, калькулятор Windows показує відповідні кнопки в режимі «Інженерний» (Науковий). Для ручного розрахунку можна використовувати метод, викладений у статті «Алгоритм знаходження кореня n-го степеня».
Для степенів вище третьої можна використовувати логарифмічну тотожність:
З неї випливає, що для добування кореня треба знайти логарифм підкореневого виразу, поділити на степінь кореня та знайти антилогарифм результату.
Корінь комплексного числа[ред. | ред. код]
Зародження поняття комплексного числа історично було пов'язано з бажанням «легалізувати» квадратні корені з від'ємних чисел. Як поступово з'ясувалося, комплексні числа володіють багатьма алгебраїчними та аналітичними властивостями; зокрема, вилучення коренів з них завжди можливо, хоча і неоднозначно.
Способи знаходження[ред. | ред. код]
Запишемо комплексне число в тригонометричної формі:
- .
Тоді корінь -го степеня з визначається формулою Муавра (тригонометрична форма) [15]:

або в показниковій формі:
(комплексне число), |
Корінь степеня з ненульового комплексного числа має значень (це наслідок основної теореми алгебри), і всі вони різні. Значення кореня, що отримане при , часто називається головним.
Оскільки для всіх значень кореня величина модуля однакова (він визначається як арифметичний корінь з модуля початкового комплексного числа), а змінюється лише його аргумент, всі значень кореня розташовуються на комплексній площині на колі радіуса з центром у початку координат. Корені ділять це коло на рівних частин.
Приклади[ред. | ред. код]
Знайдемо . Оскільки за формулою отримуємо:
При отримаємо перший корінь , при отримаємо другий корінь
Інший приклад: знайдемо .
Подамо підкорінний вираз в тригонометричній формі:
За формулою Муавра отримуємо:
У підсумку маємо чотири значення кореня[16]:
Можна записати отриману відповідь у вигляді:
Комплексна функція кореня та ріманова поверхня[ред. | ред. код]
Розглянемо комплексну функцію кореня -о степеня: Відповідно до сказаного вище, ця функція є багатозначною (точніше, -значною) функцією, і це створює незручності при її дослідженні та застосуванні. В комплексному аналізі замість розгляду багатозначних функцій на комплексній площині прийнято інше рішення: розглядати функцію як однозначну, але визначену не на площині, а на більш складному многовиді, який називається рімановою поверхнею.[17]
-
Ріманова поверхня для комплексного квадратного кореня
-
Ріманова поверхня для комплексного кореня 4-о степеня
Для комплексної функції кореня -го степеня її ріманова поверхня (див. малюнки) складається з гілок (листів), пов'язаних гвинтоподібно, причому останній лист пов'язаний з першим. Ця поверхня неперервна та однозв'язна. Один з листів містить головні значення кореня, що одержані як аналітичне продовження дійсного кореня з чисел позитивного променя дійсної осі.
Опишемо для простоти комплексну функцію квадратного кореня. Її ріманова поверхня складається з двох листів. Перший лист можна представити як комплексну площину, у якій вирізаний позитивний промінь дійсної осі. Значення функції кореня на цьому листі мають удвічі менший аргумент, ніж , і тому вони заповнюють верхню частину комплексної площини значень. На розрізі перший лист склеєний з другим, і функція неперервно продовжується через розріз на другий лист, де її значення заповнюють нижню частину комплексної площини значень. Решту вільних початок першого листа та кінець другого теж склеємо, після чого отримана функція на рімановій поверхні стає однозначною та всюди неперервною.[17]
Єдиний нуль у функції (першого порядку) виходить при . Особливі точки: та (точки розгалудження нескінченного порядку).[17] Наявність точки розгалудження означає, що замкнутий контур в околі нуля неминуче містить перехід з листа на лист.
З огляду на однозв'язність, ріманові поверхні кореня є універсальним накриттям[18] для комплексної площини без точки .
Варіації та узагальнення[ред. | ред. код]
Корінь -о степеня з є рішенням рівняння , і його в принципі можна визначити всюди, де таке рівняння має сенс. Найчастіше розглядають такі узагальнення в алгебраїчних кільцях. Найкраще досліджені узагальнені квадратні корені.
Якщо кільце — область цілісності, то квадратних коренів може бути або два, або жодного. Справді, якщо є два кореня то звідки: , тобто, в силу відсутності дільників нуля, . У більш загальному випадку, коли в кільці є дільники нуля або воно некомутативне, число коренів може бути будь-яким.
Корені для кватерніонів мають багато спільного з комплексними, але є й суттєві особливості. Квадратний кватерніонний корінь зазвичай має 2 значення, але якщо підкоренний вираз — негативне дійсне число, то значень нескінченно багато. Наприклад, квадратні корені з утворюють тривимірну сферу, яка визначається формулою[19]:
Для кільця квадратних матриць доведено, що якщо матриця позитивно визначена, то позитивно визначений квадратний корінь з неї існує та є єдиним[20]. Для матриць інших типів коренів може бути скільки завгодно (в тому числі жодного).
Квадратні корені вводяться також для функцій[21], операторів[22] та інших математичних об'єктів.
Історія[ред. | ред. код]
Розвиток поняття[ред. | ред. код]

Перші завдання, пов'язані з добуванням квадратного кореня, виявлені в працях вавилонських математиків (про досягнення стародавнього Єгипту в цьому напрямку нічого не відомо). Серед таких завдань [23]:
- Застосування теореми Піфагора для знаходження сторони прямокутного трикутника за відомими двома іншими сторонами.
- Знаходження сторони квадрата, площа якого задана.
- Розв'язування квадратних рівнянь.
Вавилонські математики (II тисячоліття до н. е.) розробили для добування квадратного кореня особливий чисельний метод. Початкове наближення для розраховувалося виходячи з найближчого до кореня (в меншу сторону) натурального числа . Представивши підкореневий вираз у вигляді: , отримуємо: , потім застосовувався ітеративний процес уточнення, що відповідає методу Ньютона [24]:
Ітерації в цьому методі дуже швидко сходяться. Для , наприклад, і ми отримуємо послідовність наближень:
У заключному значенні правильні всі цифри, крім останньої.
Аналогічні завдання і методи зустрічаються у старокитайській «Математиці у дев'яти книгах»[25]. Стародавні греки зробили важливе відкриття: — ірраціональне число. Детальне дослідження, виконане Теететом Афінським[en] (IV століття до н. Е.), показало, що якщо корінь з натурального числа не добувається без остачі, то його значення ірраціональне[26].
Греки сформулювали проблему подвоєння куба, яка зводилася до побудови кубічного кореня за допомогою циркуля і лінійки. Проблема виявилася нерозв'язною. Чисельні алгоритми вилучення кубічного кореня опублікували Герон (в трактаті «Метрика», I століття н. е.) і індійський математик Аріабхата I (V століття)[27].
Алгоритми добування коренів будь-якого степеня з цілого числа, розроблені індійськими[en] і ісламськими математиками, були вдосконалені в середньовічній Європі. Микола Орезмський (XIV століття) вперше витлумачив [28] корінь -ого степеня як піднесення до степеня .
Після появи формули Кардано (XVI століття) почалося застосування в математиці уявних чисел, що розуміються як квадратні корені з від'ємних чисел [29]. Основи техніки роботи з комплексними числами розробив в XVI столітті Рафаель Бомбеллі, який також запропонував оригінальний метод обчислення коренів (за допомогою ланцюгових дробів). Відкриття формули Муавра (1707) показало, що добування кореня будь-якого степеня з комплексного числа завжди можливо і не призводить до нового типу чисел [30].
Комплексні корені довільного степеня на початку XIX століття глибоко дослідив Гаус, хоча перші результати належать Ейлеру [31]. Надзвичайно важливим відкриттям (Галуа) стало доведення того факту, що не всі алгебраїчні числа (корені многочленів) можна отримати з натуральних за допомогою чотирьох арифметичних дій і добування кореня[32].
Етимологія терміну і походження символіки[ред. | ред. код]
Термін корінь має довгу і складну історію. Добування квадратного кореня стародавні греки розуміли строго геометрично: як знаходження сторони квадрата за відомою його площею. Після переведення на санскрит грецьке слово «сторона» перетворилася на «мула» (основа). Слово «мула» мало також значення «корінь», тому при перекладі індійських сиддхант[en] на арабський використовувався термін «джізре» (корінь рослини). Згодом аналогічне за змістом слово «radix» закріпилося в латинських перекладах з арабської, а через них і в російській математичній термінології («корінь», «радикал») [33].
Середньовічні математики (наприклад, Кардано) позначали квадратний корінь[34] символом R x, скорочення від слова «radix». Сучасне позначення вперше вжив німецький математик Крістоф Рудольфф, зі школи коссистів (тобто алгебраїстів), у 1525 році[35]. Походить цей символ від стилізованої першої літери того ж слова «radix». Риса над підкореневим виразом спочатку була відсутня; її пізніше ввів Декарт (1637) для іншої мети (замість дужок), і ця риса незабаром злилася зі знаком кореня.
Показник степеня з'явився в знаку кореня завдяки Валлісу і «Універсальній арифметиці» Ньютона (XVIII століття)[36].
Див. також[ред. | ред. код]
Література[ред. | ред. код]
- Григорій Михайлович Фіхтенгольц. Курс диференціального та інтегрального числення. — 2023. — 1900+ с.(укр.)
- Вигодський М. Я.[ru]. Справочник по элементарной математике. — изд. 25-е. — М. : Наука, 1978. — ISBN 5-17-009554-6.
- История математики, в трёх томах / Под редакцией А. П. Юшкевича. — М. : Наука, 1970—1972.
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — Москва : Наука, 1973. — 832 с.(рос.)
- Мордкович А. Г. Алгебра и начала анализа. Учебник для 10—11 классов, часть 1. — изд. 4-е. — М. : Мнемозина, 2003. — 376 с.
- Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной. — М. : Наука, 1967. — 304 с.
Примітки[ред. | ред. код]
- ↑ Корень // Математическая энциклопедия (в 5 томах). — М. : Советская Энциклопедия, 1982. — Т. 3.
- ↑ М. И. Сканави. Элементарная математика. п.1.11, стр.49.
- ↑ а б Выгодский М. Я. Справочник по элементарной математике, 1978, с. 64..
- ↑ Арифметический корень // Математическая энциклопедия (в 5 томах). — М. : Советская Энциклопедия, 1982. — Т. 1.
- ↑ Алгебричний (багатозначний) корінь у джерелах часто називають просто коренем.
- ↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966, Т. I, С. 35—36..
- ↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 141—143..
- ↑ Алгебра и начала анализа. Учебник для 10—11 классов, под ред. А. Н. Колмогорова. М.: Просвещение, 2002, С. 209.
- ↑ а б Выгодский М. Я. Справочник по элементарной математике, 1978, с. 183..
- ↑ Мордковіч А. Г., 2003.
- ↑ Фіхтенгольц Г. М. Курс диференціального й інтегрального числення, 1966, Т. I, С. 215..
- [[#cite_ref-FOOTNOTEФіхтенгольц_Г._М._Курс_диференціального_й_інтегрального_числення1966Т._I,_С._233,_окремий_випадок_для_'"`UNIQ--math-00000073-QINU`"'._12-0|↑]] Фіхтенгольц Г. М. Курс диференціального й інтегрального числення, 1966, Т. I, С. 233, окремий випадок для ..
- ↑ Не плутати з кратними інтегралами. Їх записи вельми схожі, але -й інтеграл є невизначеним, в той час як -кратний інтеграл — має певне значення.
- ↑ Фіхтенгольц Г. М. Курс диференціального й інтегрального числення, 1966, Том I, стор. 67, 131 — 132, 164, 166 — 167..
- ↑ Корн Г., Корн Т. Довідник з математики, 1973.
- ↑ Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — издание третье, стереотипное. — М. : Наука, 1976. — С. 68.
- ↑ а б в Свєшніков А. Г., Тихонов А. Н. Теорія функцій комплексної змінної, 1967.
- ↑ Болтянский В. Г., Ефремович В. А. Наглядная топология. — М. : Наука, 1982. — С. 112.
- ↑ Porteous, Ian R. Clifford Algebras and the Classical Groups. Cambridge, 1995, page 60.
- ↑ Див., наприклад: Гантмахер Ф. Р.. Теория матриц. М.: ГИТТЛ, 1953, С. 212—219, или: Воеводин В., Воеводин В. Энциклопедия линейной алгебры. Электронная система ЛИНЕАЛ. Спб.: БХВ-Петербург, 2006.
- ↑ См., наприклад: Ершов Л. В., Райхмист Р. Б. Построение графиков функций. М.: Просвещение, 1984, или: Каплан И. А. Практические занятия по высшей математике. Харьков: Изд-во ХГУ, 1966.
- ↑ Див., наприклад: Хатсон В., Пим Дж. Приложения функционального анализа и теории операторов. М.: Мир, 1983, или: Халмош П. Гильбертово пространство в задачах. М.: Мир, 1970.
- ↑ Історія математики, 1970-1972, Том I, С. 42-46..
- ↑ Історія математики, 1970-1972, Том I, С. 47..
- ↑ Історія математики, 1970-1972, Том I, С. 169-171..
- ↑ Башмакова І. Г. Становлення алгебри (з історії математичних ідей). — М. : Знання, 1979. — С. 23. — (Нове у житті, науці, техніці. Математика, кібернетика, № 9)
- ↑ Abhishek Parakh. Ariabhata's root extraction methods // Indian Journal of History of Science. — 2007. — Вип. 42.2. — С. 149-161. Архівовано з джерела 9 червня 2010. Процитовано 2015-05-30.
- ↑ Історія математики, 1970-1972, Том I, С. 275-276..
- ↑ Історія математики, 1970-1972, Том I, С. 296-298..
- ↑ Історія математики, 1970-1972, Том III, С. 56-59..
- ↑ Історія математики, 1970-1972, Том III, С. 62..
- ↑ Колмогоров А. Н., Юшкевич А. П. (ред.). {{{Заголовок}}}. — М., 1978. — С. 58-66.
- ↑ Історія математики, 1970-1972, Том I, С. 185..
- ↑ Нікіфоровський В. А. З історії алгебри XVI-XVII ст. — М., 1979. — С. 81. — (Історія науки і техніки)
- ↑ Знаки математичні // Математична енциклопедія. — М. : Радянська Енциклопедія.
- ↑ Александрова Н. В. Історія математичних термінів, понять, позначень: Словник-довідник, вид. 3-е. — СПб. : ЛКІ. — С. 82. — ISBN 978-5-382-00839-4.





![{\displaystyle b={\sqrt[{n}]{a}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/faa9d021810625038d355d8d04e49225a5f25121)
![{\displaystyle {\sqrt[{2}]{9}}=\pm 3,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6c68e659a7a99332be1cfa67dd7c2ad9ebb9af3)

![{\displaystyle {\sqrt[{3}]{\ 64}}=4,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20c4beeb304fe77e586206e908c1ee4f7b6f267c)

![{\displaystyle {\sqrt[{3}]{\frac {8}{27}}}={\frac {2}{3}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6bdc22590a600d2eedc6841477696f1ae07ed9a)





![{\displaystyle {\sqrt[{n}]{a}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7873203eb76042fcd24056c553de8c86054a2df)



![{\displaystyle {\sqrt[{3}]{a}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a8092bee1ed820e5f8f1d7a2d8696c53a55fea7)
![{\displaystyle {\sqrt[{3}]{a}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/895424fc79dfd221f984d973ac95ca277bd0e60c)
![{\displaystyle {\sqrt[{n}]{a}}=b}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a689688935f6bb305cb30a3f4d178cc01d49bb9)

![{\displaystyle {\sqrt[{3}]{125}}=5,\ {\sqrt[{5}]{32}}=2,\ {\sqrt[{15}]{1}}=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f472c8c6ad0d90dd45000ab47233f55ef5cbe42d)

![{\displaystyle {\sqrt[{3}]{-8}}=-2,\ {\sqrt[{5}]{-243}}=-3,\ {\sqrt[{7}]{-1}}=-1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e37b2821a200bbf758c4661d5b13ee407a3d2f9)
![{\displaystyle {\sqrt[{n}]{a}}=\pm b}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf21563d513e7b8292a2e4eea8618aa3bbfcfbc9)
![{\displaystyle {\sqrt {4}}=\pm 2,\ \ {\sqrt[{4}]{81}}=\pm 3,\ \ {\sqrt[{10}]{1024}}=\pm 2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97d8feb54f099cefffd682affe2e09ff8fb84460)

![{\displaystyle {\sqrt[{n}]{0}}=0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c650afa98b96756d746750fcaac8f71275a749a5)




![{\displaystyle ~{\sqrt[{n}]{a^{n}}}=a}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ea05853a32f82345a32fb5e1adede2791dcf981)
![{\displaystyle ~{\color {blue}{\sqrt[{\color {black}n}]{\color {black}{a^{n}}}}}=|a|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a69899cd897a51a310e737332237ddf4bedb7d6)

![{\displaystyle {\color {blue}{\sqrt[{\color {black}n}]{\color {black}{a}}}}<{\color {blue}{\sqrt[{\color {black}n}]{\color {black}{b}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd8a577e4f3d79fce7791fe7b6242a87c959c07a)
![{\displaystyle {\color {blue}{\sqrt[{\color {black}n}]{\color {black}{ab}}}}={\color {blue}{\sqrt[{\color {black}n}]{\color {black}{a}}}}{\color {blue}{\sqrt[{\color {black}n}]{\color {black}{b}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab4f987edd67897546b66a0aa8ce41595459a135)
![{\displaystyle {\color {blue}{\sqrt[{\color {black}n}]{\color {black}{\frac {a}{b}}}}}={\frac {\color {blue}{\sqrt[{\color {black}n}]{\color {black}{a}}}}{\color {blue}{\sqrt[{\color {black}n}]{\color {black}{b}}}}},\;b\neq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3710335cb407ed4643e06a4971fea8d03f50837a)
![{\displaystyle a^{m/n}={\color {blue}{\sqrt[{\color {black}n}]{\color {black}{a^{m}}}}}=\left({\color {blue}{\sqrt[{\color {black}n}]{\color {black}{a}}}}\right)^{m}=\left(a^{1/n}\right)^{m}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37615b317944b42c53b5de05431bc3369c3f59af)
![{\displaystyle {\color {blue}{\sqrt[{\color {black}nk}]{\color {black}{a^{mk}}}}}={\color {blue}{\sqrt[{\color {black}n}]{\color {black}{a^{m}}}}},\;n,k\in \mathbb {N} .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf6d3911501828794dae6ce86de52f73bcf0e394)
![{\displaystyle {\color {blue}{\sqrt[{\color {black}6}]{\color {black}{64}}}}={\color {blue}{\sqrt[{\color {black}{2\cdot 3}}]{\color {black}{4^{3}}}}}={\color {blue}{\sqrt {\color {black}{4}}}}=2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c63d5e94e829da11f858861200e5fcada0281e5b)
![{\displaystyle {\color {blue}{\sqrt[{\color {black}n}]{\color {blue}{\sqrt[{\color {black}k}]{\color {black}{a}}}}}}={\color {blue}{\sqrt[{\color {black}nk}]{\color {black}{a}}}},\;n,k\in \mathbb {N} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/517671f0dec2d95e82a201cbc45fa0991da424da)
![{\displaystyle {\sqrt[{n}]{-a}}=-{\sqrt[{n}]{a}},\quad n-}](https://wikimedia.org/api/rest_v1/media/math/render/svg/beb445b684626d4ac50dc5611bdf08addbe47490)


![{\displaystyle a^{\frac {m}{n}}={\color {blue}{\sqrt[{\color {black}n}]{\color {black}{a^{m}}}}},\quad >0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2b3d36ecc24120eae14d26e897cf32a5df21e57)


![{\displaystyle ~{\color {blue}{\sqrt[{\color {black}n}]{\color {black}{a}}}}=a^{\frac {1}{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55d3d768fc893886b3c71670121c5c727ce6e51c)

![{\displaystyle [0;\ 1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bd9d07c3fa150a68ff70c59f5360476fd970cdc)
![{\displaystyle y={\sqrt[{n}]{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70c948f50917ced2d3036c8c5edc92ee14a6b43a)



![{\displaystyle {\frac {d}{dx}}{\sqrt[{n}]{x}}={\frac {1}{n{\sqrt[{n}]{x^{n-1}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8cc55cd5fb693a81abf8db7397751adb98e61ada)

![{\displaystyle \int {\sqrt[{n}]{x}}\;dx={\frac {\sqrt[{n}]{x^{n+1}}}{1+{\frac {1}{n}}}}+C}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7660278dbc7fb62945550218b8c93f2c9beca94)



![{\displaystyle {\sqrt[{n}]{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b3ba2638d05cd9ed8dafae7e34986399e48ea99)
![{\displaystyle {\frac {d^{k}}{dx^{k}}}{\sqrt[{n}]{x}}=(-1)^{k}{\frac {\prod _{m=0}^{k-1}(mn-1)}{{n^{k}}{\sqrt[{n}]{x^{kn-1}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff6f3373038a13a0c053735d14061dfb06a12c19)

![{\displaystyle \underbrace {\int \cdots \int } _{k}{\sqrt[{n}]{x}}\ \underbrace {dx\cdots dx} _{k}={\frac {{n^{k}}{\sqrt[{n}]{x^{kn+1}}}}{\prod _{m=1}^{k}(1+mn)}}+C}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c96db30a93c29ef7b7efcc58d922ad92de149be)

![{\displaystyle \lim _{n\to \infty }{\sqrt[{n}]{n}}=\lim _{n\to \infty }{\sqrt[{n}]{\ln n}}=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f0e1e5e54014face5332313d4e1aefc3e6860fb)
![{\displaystyle \lim _{n\to \infty }n\left({\sqrt[{n}]{x}}-1\right)=\lim _{n\to \infty }n\left(1-{\frac {1}{\sqrt[{n}]{x}}}\right)=\ln x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83d95e2439ebe22e00bd6addcf35e3377c462c23)
![{\displaystyle \lim _{x\to 0}{\frac {{\sqrt[{n}]{(x+1)^{m}}}-1}{x}}={\frac {m}{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d69c07700c69c3c6ea11288bea5bc3b878ae7fc)
![{\displaystyle \lim _{n\to \infty }\left({\frac {{\sqrt[{n}]{a}}+{\sqrt[{n}]{b}}}{2}}\right)^{n}={\sqrt {ab}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59682d9b7c62b477d266fd422777cc3a7235143f)
![{\displaystyle \log _{a}{\sqrt[{n}]{x}}={\frac {\log _{a}(x)}{n}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf9ed8d2e6494237c46de81c3e9c094c23f6834a)


![{\displaystyle {\sqrt[{n}]{z}}={\color {blue}{\sqrt[{\color {black}n}]{\color {black}{r}}}}\left(\cos {\frac {\varphi +2\pi k}{n}}+i\sin {\frac {\varphi +2\pi k}{n}}\right),\;k=0,1,\dots ,n-1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc11b927d2f38f305cd20979de988aa1774ff8a2)

![{\displaystyle {\sqrt[{n}]{z}}={\color {blue}{\sqrt[{\color {black}n}]{\color {black}{r}}}}e^{\left(i{\frac {\varphi +2\pi k}{n}}\right)},\;k=0,1,\dots ,n-1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35e72ba1ad691361f19ffb12c7cb738edadb1840)








![{\displaystyle {\color {blue}{\sqrt[{\color {black}n}]{\color {black}{r}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d735d37172f368d019ceb8f67b7cd38a5982c58a)






![{\displaystyle {\sqrt[{4}]{-16}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b16dc4a185ac1049e43e6ad7372e8f9686312dc)

![{\displaystyle z_{k}={\sqrt[{4}]{-16}}={\sqrt[{4}]{16}}\left(\cos {\frac {\pi +2k\pi }{4}}+i\sin {\frac {\pi +2k\pi }{4}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b48ba51e9b2752410472bc400a9513268ba46aaf)




![{\displaystyle ~{\sqrt[{4}]{-16}}={\sqrt {2}}\ (\pm 1\pm i)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0282d0c39ac3b013c3b416adf3857dff88ef6c1c)
![{\displaystyle w={\sqrt[{n}]{z}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe2a25829482fe1c9b8dd10f629067ba547992af)























