Теорема про гомоморфізми

Теорема про гомоморфізми — фундаментальна теорема про структуру двох об'єктів між якими заданий гомоморфізм, а також про ядро та образ гомоморфізму.

Застосовується для доведення теорем про ізоморфізми.

Існуює версія теореми для груп, моноїдів, кілець, модулів, векторних просторів та інших алгебраїчних структур.

Групи

Якщо φ: G → H гомоморфізм груп, K — нормальна підгрупа в G, φ — натуральний сюр'єктивний гомоморфізм G → G/K.

І якщо K ⊂ ker(f), тоді існує єдиний гомоморфізм h: G/K → H такий, що f = h φ.

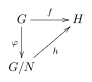
Ця теорема описується комутативною діаграмою:

Література

• А.Г. Курош «Общая алгебра», — М.: Мир, 1973, 162 с
• П. Кон «Универсальная алгебра», — М.: Мир, 1969, 351 с