Формула Борда-Карно

Формула (теорема) Борда-Карно — у гідродинаміці це емпірична формула, що описує втрати механічної енергії рідини у зв'язку із раптовим розширенням потоку. Вона описує, як знижується повний напір у зв'язку із втратами. Це рівняння, на відміну від рівняння Бернуллі для ідеальної рідини, де загальна питома енергія рідини стала уздовж лінії течії дозволяє розрахувати втрати на місцевому гідравлічному опорі. Це рівняння назване на честь Жана-Шарля де Борда (Jean-Charles de Borda) (1733–1799) та Лазара Карно (Lazare Nicolas Marguerite Carnot) (1753–1823).

Це рівняння використовується як для відкритого (безнапірного) потоку у каналі, так і для потоків у трубах (напірних потоків).

Формулювання

Формула Борда-Карно має вигляд:

$\Delta E\,=\,\xi \,{\scriptstyle {\frac {1}{2}}}\,\rho \,\left(V_{1}\,-\,V_{2}\right)^{2},$

Де

ΔE — втрата механічної енергії рідиною;

ξ  — емпіричний безрозмірний коефіцієнт втрат, що набуває величину між нулем і одиницею, 0 ≤ ξ ≤ 1;

ρ — густина рідини;

V₁ і V₂ — середня швидкість потоку перед і за раптовим розширенням відповідно.

У випадку раптового розширення коефіцієнт втрат дорівнює одиниці. В інших випадках, коефіцієнт втрат повинен бути визначений за допомогою інших засобів, найчастіше з використанням емпіричної формули (на основі даних, отриманих дослідним шляхом). Формула Брода-Карно для розрахунку втрат енергії справедлива для випадку зменшення швидкості,V ₁ >V₂, в іншому випадку втрати ΔE прямують до нуля (без додаткової механічної роботи сил тертя).

Приклади застосування

Раптове розширення потоку у трубі

Раптове розширення потоку.

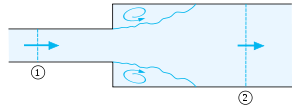
Формула Борда-Карно може бути застосована для розрахунку втрат енергії для потоку, що проходить через раптове розширення горизонтальної труби. У перетині 1 середня швидкість потоку дорівнює V₁, тиск становить p₁ і площа поперечного перерізу S₁. Відповідні величини для потоку у перетині 2 — після розширення становлять V₂, p₂ і S₂, відповідно. Коефіцієнт втрат ξ для цього раптового розширення дорівнює одиниці :ξ = 1,0. Виходячи із закону збереження маси, вважаючи сталою густину рідини ρ, об'ємна витрата через обидва перерізи повинна бути однаковою (умова нерозривності):

$S_{1}\,V_{1}\,=S_{2}\,V_{2}$     звідки     $V_{2}\,=\,{\frac {S_{1}}{S_{2}}}\,V_{1}.$

Отже, згідно з формулою Борода-Карно, втрати механічної енергії в цьому раптовому розширенні:

$\Delta E\,=\,{\frac {1}{2}}\,\rho \,\left(1\,-\,{\frac {S_{1}}{S_{2}}}\right)^{2}\,V_{1}^{2}.$

Відповідні втрати напору ΔH будуть:

$\Delta H\,=\,{\frac {\Delta E}{\rho \,g}}\,=\,{\frac {1}{2\,g}}\,\left(1\,-\,{\frac {S_{1}}{S_{2}}}\right)^{2}\,V_{1}^{2}={\frac {\left(V_{1}-V_{2}\right)^{2}}{2g}}.$

Для цього випадку ξ = 1, уся зміна кінетичної енергії між двома перерізами розсіюється у вигляді тепла. Останній вираз ще називають формулою Борда. Ж.Борда отримав її в 1776р. Згідно з нею, втрати напору при раптовому розширенні дорівнюють швидкісному напору, підрахованому за втраченою швидкістю, так як різницю $(V_{1}-V_{2})$ називають втраченою швидкістю.

На основі запису рівняння Бернуллі для двох перерізів можна отримати вираз для визначення зміни тиску між цими перерізами для горизонтальної труби:

$\Delta p\,=\,p_{1}\,-\,p_{2}\,=\,-\,\rho \,{\frac {S_{1}}{S_{2}}}\left(1\,-\,{\frac {S_{1}}{S_{2}}}\right)\,V_{1}^{2},$

або у напорах:

$\Delta h\,=\,h_{1}\,-\,h_{2}\,=\,-\,{\frac {1}{g}}\,{\frac {S_{1}}{S_{2}}}\left(1\,-\,{\frac {S_{1}}{S_{2}}}\right)\,V_{1}^{2}.$

Мінус перед правою частиною рівняння, означає, що тиск (напір) є більшим після розширення труби. Те, що ця зміна тиску (напору), безпосередньо до і після розширення труби разом з втратою енергії на розсіювання відповідає зменшенню кінетичної енергії між відповідними перерізами випливає із рівняння Бернуллі.

Раптове звуження труби

У потоці за раптовим звуженням у перерізі 3 спостерігається відрив потоку

У випадку раптового зменшення діаметра труби, потік не в змозі відтворити перехід до профілю вузької трубу. У результаті спостерігається зрив потоку, що приводить до появи завихрень біля входу у вузьку трубу. Основний потік спочатку звужується у перерізі 3, а потім знову розширюється, щоб покрити всю область труби у перерізі 2.

Між перетином 1 і перетином 3, у якому основний потік стискається найбільше втрати енергії незначні і ними нехтують. Але існують значні втрати в потоці, що розширюється від перерізу 3 до перерізу 2. Ці втрати напору можна виразити за допомогою формули Брода-Карно рівняння з врахуванням коефіцієнта стиснення потоку ε

$\epsilon \,=\,{\frac {S_{3}}{S_{2}}},$

де S₃ — площа перерізу потоку у зоні найбільшого стиснення (переріз 3);

S₂ — площа перерізу труби меншого діаметра (переріз 2).

Оскільки S₃ ≤ S₂, коефіцієнт стиснення потоку ε ≤ 1 то на основі закону збереження маси при сталій густині (рідина нестискувана):

$S_{1}\,V_{1}\,=\,S_{2}\,V_{2}\,=\,S_{3}\,V_{3},$

де V₁, V₂ and V₃ середні швидкості у відповідних перерізах потоку. Тоді згідно з формулою Борда-Карно (при коефіцієнті втрат ξ=1) втрат питомої енергії ΔEна одиницю об'єму рідини:

$\Delta E\,=\,{\frac {1}{2}}\,\rho \,\left(V_{3}\,-\,V_{2}\right)^{2}\,=\,{\frac {1}{2}}\,\rho \,\left({\frac {1}{\epsilon }}\,-\,1\right)^{2}\,V_{2}^{2}\,=\,{\frac {1}{2}}\,\rho \,\left({\frac {1}{\epsilon }}\,-\,1\right)^{2}\,\left({\frac {S_{1}}{S_{2}}}\right)^{2}\,V_{1}^{2}.$

Відповідні втрати напору ΔH можуть бути обчислені як ΔH = ΔE/(ρg).

Згідно з дослідженнями Ю. Вейсбаха (J. Weisbach), коефіцієнт стиснення для звуження з гострими краями становить приблизно:

$\epsilon \,=\,0.63\,+\,0.37\,\left({\frac {S_{2}}{S_{1}}}\right)^{3}.$

Джерела

• Левицький Б. Ф., Лещій Н. П. Гідравліка. Загальний курс. — Львів: Світ, 1994. — 264с. ISBN 5-7773-0158-4
• Константінов Ю. М., Гіжа О. О. Технічна механіка рідини і газу: Підручник.- К.: Вища школа, 2002.-277с.: іл. ISBN 966-642-093-7
• Кулінченко В. Р. Гідравліка, гідравлічні машини і гідропривід: Підручник.- Київ: Фірма «Інкос», Центр навчальної літератури, 2006.-616с. ISBN 966-8347-38-2
• Колчунов В. І. Теоретична та прикладна гідромеханіка: Навч. Посібник.-К.: НАУ, 2004.-336с. ISBN 966-598-174-9

Див. також

• Дифузор
• Гідравлічний опір
• Формула Дарсі-Вейсбаха