Цикл Ленуара

Газовий поршневий двигун Ленуара (1860)

Цикл Ленуа́ра (англ. Lenoir cycle) — термодинамічний цикл, що описує робочі процеси низки двигунів внутрішнього згоряння, різного конструктивного виконання та призначення, до яких належать:

• історично перший роботоздатний двигун внутрішнього згоряння, запатентований у 1859 р. бельгійським винахідником Жаном Жозефом Етьеном Ленуаром, на честь якого цикл отримав свою назву;
• теплові ракетні двигуни;
• безклапанні пульсуючі повітряно-реактивні двигуни;
• газотурбінні двигуни внутрішнього згоряння, що працюють без доступу атмосферного повітря, на ракетному пальному, (однокомпонентному, наприклад, перекису водню, або двокомпонентному, що складається з пального і окислювача), наприклад, турбіни двигунів торпед, турбонасосних агрегатів рідинних реактивних двигунів тощо.

Опис

p-V діаграма циклу Ленуара

Стадії роботи безклапанного повітряно-реактивного двигуна

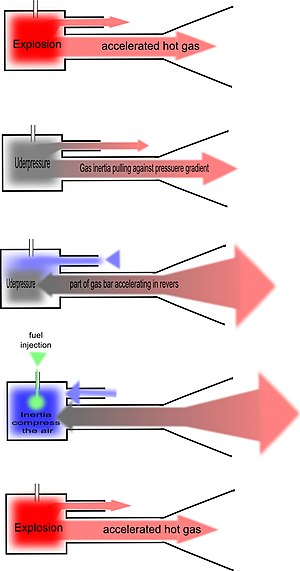
Ідеальний цикл Ленуара складається з трьох термодинамічних процесів:

• 1—2 ізохорне нагрівання робочого тіла;
• 2—3 ізоентропійне розширення;
• 3—1 ізобарне охолодження.

Ізохорне підведення тепла (1-2)

Для випадку ідеального газу за типового циклу Ленуара перший такт (1-2) передбачає підведення теплоти при постійному об'ємі. Відповідно до першого закону термодинаміки:

${}_{1}Q_{2}=mc_{v}\left({T_{2}-T_{1}}\right)$.

На цьому такті робота не виконується тому що об'єм залишається сталим:

${}_{1}W_{2}=\int \limits _{1}^{2}{pdV}=0$

І за умови сталого об'єму теплоємність ідеального газу:

$c_{v}={\frac {R}{k-1}}$,

де R — універсальна газова стала ідеального газу;

k — показник адіабати (k = 1,4 для повітря приблизно). Тиск після підведення тепла може бути обчислена з рівняння стану ідеального газу: $p_{2}V_{2}=RT_{2}$

Ізоентропійне розширення (2-3)

Другий такт (2-3) включає зворотне адіабатичне розширення робочого тіла до досягнення початкового тиску. Процес може бути описаний відповідно до другого закону термодинаміки наступним чином:

${\frac {T_{2}}{T_{3}}}=\left({\frac {p_{2}}{p_{3}}}\right)^{\textstyle {{k-1} \over k}}=\left({\frac {V_{3}}{V_{2}}}\right)^{k-1}$,

де $p_{3}=p_{1}$ для умов перебігу цього такту. Рівняння перший закон термодинаміки набуде вигляду для цього випадку розширення: ${}_{2}W_{3}=mc_{v}\left({T_{2}-T_{3}}\right)$ оскільки для адіабатичного процесу: ${}_{2}Q_{3}=0$.

Ізобарне охолодження (3-1)

На останньому такті (3-1) відбувається охолодження до початкової температури при постійному тиску. З першого закону термодинаміки можна знайти: ${}_{3}Q_{1}-_{3}W_{1}=U_{1}-U_{3}$.

З визначення роботи: ${}_{3}W_{1}=\int \limits _{3}^{1}{pdV}=p_{1}\left({V_{1}-V_{3}}\right)$, буде витрачена наступна кількість теплової енергії за цей такт: ${}_{3}Q_{1}=\left({U_{1}+p_{1}V_{1}}\right)-\left({U_{3}+p_{3}V_{3}}\right)=H_{1}-H_{3}$.

В результаті, можна визначити відведене тепло як: ${}_{3}Q_{1}=mc_{p}\left({T_{1}-T_{3}}\right)$ з визначення теплоємності ідеального газу при сталому тиску: $c_{p}={\frac {k}{k-1}}$.

Загальна фективність циклу Ленуара визначається корисною роботою від підведеної теплової енергії за цикл і дорівнює $\eta _{th}={\frac {{}_{2}W_{3}+{}_{3}W_{1}}{{}_{1}Q_{2}}}$. Слід відзначити, що корисна робота виконується під час такту розширення (2-3) і частина енергії втрачається під час такту охолодження (3-1).

Термічний ККД

Термічний коефіцієнт корисної дії ідеального циклу Ленуара можна обчислити з використанням одного з наведених нижче еквівалентних рівнянь:

$\eta =1-k{\frac {n-1}{n^{k}-1}}$,

де $\,n={\frac {V_{3}}{V_{1}}}$ — ступінь розширення;

$\,k$ — показник адіабати для робочого тіла.

Цією формулою зручно користуватись для визначення ККД поршневого двигуна Ленуара, оскільки параметр $\,n$ легко визначається з геометрії й кінематики вузла циліндр-поршень двигуна.

$\eta =1-k{\frac {\lambda ^{1/k}-1}{\lambda -1}}$,

тут $\,\lambda ={\frac {p_{2}}{p_{1}}}$ — ступінь підвищення тиску.

Ця формула найчастіше використовується для розрахунку ККД реактивних і газотурбінних двигунів, що працюють за циклом Ленуара.

Див. також

• Двигун Ленуара
• Цикл Гамфрі

Джерела

• Швець І. Т. , Кіраковський Н. Ф. Загальна теплотехніка та теплові двигуни. — К.: Вища школа, 1977. — 269 с.
• Корець, М. С. Машинознавство: Основи гідравліки та теплотехніки. Гідравл.машини та теплові двигуни: навч.посіб.для студ. / М. С. Корець. — К: Знання України, 2001. — 448 с. — ISBN 966-618-153-3
• Жележко Б. Е. и др. Термодинамика, теплоотдача и двигатели внутреннего сгорания. — Минск: Высшая школа., 1985. — 271 с.

Посилання

• R.K.Rajput A Textbook of Internal Combustion Engines (англ.)