Вейвлет-перетворення

Приклад 2D дискретного вейвлет-перетворення, яке використовується в JPEG 2000.

В математиці, серії вейвлетів є подання квадратної інтегрованої (дійсні або комплексні значення) функції за певною ортонормованої серії, породженої вейвлетом. В даний час, вейвлет-перетворення є одним з найпопулярніших тимчасових частот-перетворювань. У даній статті наводиться формальне та математичне визначення ортонормованого вейвлета, та інтегрального вейвлет-перетворення.

Визначення

Функція $\scriptstyle \psi \,\in \,L^{2}(\mathbb {R} )$ називається ортонормованим вейвлетом, якщо її можна використати для визначення базису Гільберта, тобто повна ортонормована система, для Гільбертого простору $\scriptstyle L^{2}\left(\mathbb {R} \right)$ квадратично-інтегрованих функцій. Базис Гільберта будується як сімейство функцій $\scriptstyle \{\psi _{jk}:\,j,\,k\,\in \,\mathbb {Z} \}$ за допомогою двійкових перенесень і розтягувань $\scriptstyle \psi \,$,

$\psi _{jk}(x)=2^{\frac {j}{2}}\psi \left(2^{j}x-k\right)\,$ для цілих j, k. Якщо під стандартним передгільбертовим простором на $\scriptstyle L^{2}\left(\mathbb {R} \right)$,

$\langle f,g\rangle =\int _{-\infty }^{\infty }f(x){\overline {g(x)}}dx$ то це сімейство ортонормоване і його система теж ортонормована: :${\begin{aligned}\langle \psi _{jk},\psi _{lm}\rangle &=\int _{-\infty }^{\infty }\psi _{jk}(x){\overline {\psi _{lm}(x)}}dx\\&=\delta _{jl}\delta _{km}\end{aligned}}$

де $\scriptstyle \delta _{jl}\,$, є дельта Кронекера. Повнота виконується, якщо кожна функція $\scriptstyle h\,\in \,L^{2}\left(\mathbb {R} \right)$ може бути розширена в базисі як

$h(x)=\sum _{j,k=-\infty }^{\infty }c_{jk}\psi _{jk}(x)$

із збіжності рядів розуміється збіжність по нормі. Таке уявлення функції f відомо як серія вейвлета. Це означає, що ортонормований вейвлет самоподвійний. Інтегральне вейвлет-перетворення є інтегральним перетворенням і визначається як : $\left[W_{\psi }f\right](a,b)={\frac {1}{\sqrt {|a|}}}\int _{-\infty }^{\infty }{\overline {\psi \left({\frac {x-b}{a}}\right)}}f(x)dx\,$. Коефіцієнти вейвлетів $\scriptstyle c_{jk}$ отримуються з формули: $c_{jk}=\left[W_{\psi }f\right]\left(2^{-j},k2^{-j}\right)$ Тут, $\scriptstyle a\;=\;2^{-j}$ називається бінарним розширенням або двійковим розширенням, і $\scriptstyle b\;=\;k2^{-j}$ це бінарна або двійкова позиція.

Принцип

Основна ідея вейвлет-перетворень є те, що перетворення має дозволити тільки зміни в продовження часу, але не форму. Це залежить від вибору відповідних базисних функцій, які дозволяють це. Зміни в продовження часу, як очікується, відповідають відповідній частоті аналізу функції базису. Виходячи з принципу невизначеності обробки сигналів:$\Delta t\Delta \omega \geqq {\frac {1}{2}}$, де t представляє час і ω кутову частоту; (ω = 2πf, де f є тимчасова частота). Чим вище необхідний дозвіл в часі, тим нижче має бути дозвіл по частоті. Чим більше вибрано розширення вікна аналізу, тим більше величина .

Коли Δt велике,

1. Поганий дозвіл за часом.
2. Гарний дозвіл по частоті.
3. Низька частота, великий коефіцієнт масштабування.

Коли Δt мала

1. Гарний дозвіл за часом.
2. Поганий дозвіл по частоті.
3. Висока частота, малий коефіцієнт масштабування.

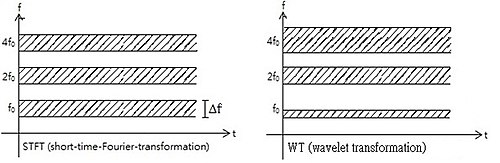
Іншими словами, базову функцію Ψ можна розглядати як імпульсний відгук системи, з якою функція х(t) була відфільтрована. Перетворений сигнал містить інформацію про час і частоту. Таким чином, вейвлет-перетворення містить інформацію, аналогічну до віконного Фур'є-перетворення, але з додатковими спеціальними властивостями вейвлетів, які з'являються в вирішенні під час більш високих частотах аналізу базисної функції. Різниця в дозволі часу на висхідних частотах для перетворення Фур'є і вейвлет-перетворення показано нижче.

Можна побачити, що вейвлет-перетворення кращий в дозволі часу високих частот, в той час як для повільно мінливих функцій, важливий дозвіл по частоті. Інший приклад: Аналіз трьох накладених один на одного синусоїдальних сигналів $\scriptstyle y(t)\;=\;\sin(2\pi f_{0}t)\;+\;\sin(4\pi f_{0}t)\;+\;\sin(8\pi f_{0}t)$, з STFT і вейвлет-перетворенням.

Вейвлет стиснення

Вейвлет стиснення є формою стиснення даних, яка добре підходить для стиснення зображень (іноді також стиснення відео і аудіо стиснення). Помітні реалізацій JPEG 2000, DjVu і нерухомих зображень, CineForm і BBC's Dirac. Мета полягає в тому, щоб зберігати дані зображення, зайнявши, при цьому як менше місця, наскільки це можливо в файлі. Вейвлет стиснення може бути або без втрат, або з втратами.

За допомогою вейвлет-перетворення, методи вейвлет стиснення є достатніми для подання перехідних процесів, таких як ударні звуки в аудіо, або високочастотні компоненти в двовимірних зображень, наприклад, зображення зірок на нічному небі. Це означає, що перехідні елементи даних сигналу можуть бути представлені меншою кількістю інформації, ніж було б у разі використання якої-небудь іншої трансформації, наприклад широкого дискретного косинусного перетворення.

Дискретне вейвлет-перетворення було успішно застосовано для стиснення електрокардіографічних (ЕКГ) сигналів. У даній роботі, висока кореляція між відповідними вейвлет-коефіцієнтами сигналів послідовних серцевих циклів і використовуються лінійне передбачення з використанням.

Вейвлет стиснення не підходить для всіх видів даних: перехідні характеристики сигналу означають гарне стиснення вейвлета, в той час як гладкі, періодичні сигнали краще стискаються за допомогою інших методів, зокрема, традиційна гармоніка стиснення (частотна область, за допомогою перетворень Фур'є і пов'язаними з ними).

Дивись Щоденник x264 Розробник: Проблеми з вейвлетами (2010) (Diary Of An x264 Developer: The problems with wavelets) для обговорення практичних питань існуючих методів з використанням вейвлетів для стиснення відео.

Метод

Перше вейвлет-перетворення було прикладним. Він виробляє стільки коефіцієнтів, скільки пікселів у зображенні (тобто, немає ніякого стиснення, оскільки це тільки перетворення). Ці коефіцієнти можна легше стиснути, тому що загальна матриця містить надлишкову інформацію, а значення їх — статистично залежні. Цей принцип називається кодування з перетворенням. Після цього коефіцієнти квантуються і квантовані значення ентропійно кодуються і / або кодується довжина послідовності. Декілька 1D і 2D застосувань вейвлет-стиснення використовують технологію, яка називається «вейвлетний слід» (англ. wavelet footprints).

Порівняння з перетворенням Фур'є та частотно-часового аналізу

Перетворення	Представлення	Вхідні дані
Перетворення Фур'є	${\hat {f}}(\xi )=\int _{-\infty }^{\infty }f(x)e^{-2\pi ix\xi }\,dx$	ξ, частота
Частотно-часовий аналіз	$X(t,f)$	t, time; f, частота
Вейвлет-перетворення	$X(a,b)={\frac {1}{\sqrt {a}}}\int _{-\infty }^{\infty }{\overline {\Psi \left({\frac {t-b}{a}}\right)}}x(t)\,dt$	a, масштаб; b, час

Вейвлети мають деякі незначні переваги в порівнянні з Фур'є, наприклад, в скороченні обчислень при розгляді конкретних частот. Проте, вони рідко бувають більш чутливими, і, дійсно, спільний вейвлет Морлета — це математично ідентичний до віконного перетворення Фур'є з використанням функції вікна Гаусса. Виняток є при пошуку сигналів відомої синусоїдальної форми (наприклад, серцебиття); в цьому випадку, використовуючи відповідний вейвлет можна перевершити стандартний аналіз STFT / Морлет.

Інші практичні використання

Вейвлет-перетворення може дати нам з частотою сигналів час, пов'язаним з цими частотами, робить його дуже зручним для його застосування в різних областях. Так, наприклад, обробка сигналів прискорень для аналізу ходи, для виявлення несправностей, для дизайну електрокардіостимуляторів низької потужності, а також в надширокосмугових (Сніп) бездротового зв'язку.

1.Дискретизація c-τ осі

Застосовують наступну дискретизацію частоти і часу:

${\begin{aligned}c_{n}&=c_{0}^{n}\\\tau _{m}&=m\cdot T\cdot c_{0}^{n}\end{aligned}}$

Призводить до форми вейвлетів, яка є дискретна формулою для базису вейвлета: $\Psi (k,n,m)={\frac {1}{\sqrt {c_{0}^{n}}}}\cdot \Psi \left[{\frac {k-mc_{0}^{n}}{c_{0}^{n}}}T\right]={\frac {1}{\sqrt {c_{0}^{n}}}}\cdot \Psi \left[\left({\frac {k}{c_{0}^{n}}}-m\right)T\right]$

Такі дискретні вейвлети можуть бути використані для трансформації:

$Y_{DW}(n,m)={\frac {1}{\sqrt {c_{0}^{n}}}}\cdot \sum _{k=0}^{K-1}y(k)\cdot \Psi \left[\left({\frac {k}{c_{0}^{n}}}-m\right)T\right]$

2.Реалізація через БПФ (швидке перетворення Фур'є)

Видно з подання вейвлет-перетворення (як показано нижче) :$Y_{W}(c,\tau )={\frac {1}{\sqrt {c}}}\cdot \int _{-\infty }^{\infty }y(t)\cdot \Psi \left({\frac {t-\tau }{c}}\right)\,dt$

де с — коефіцієнт масштабування, τ являє собою фактор зсуву часу і, як вже згадувалися в цьому контексті, вейвлет-перетворення відповідає згортку функції у(t) і вейвлет-функцію]. Згортка може бути реалізована як множення в частотній області. При цьому наступний підхід результатів реалізації в:

1. Фур'є-перетворення сигналу у(к) з FFT.
2. Вибір дискретного коефіцієнта масштабування $c_{n}$.
3. Масштабування базису вейвлет-функції за допомогою цього чинника $c_{n}$ і результат швидкого перетворення Фур'є цієї функції.
4. Множення з перетвореним сигналом YFFT з першого кроку.

№Зворотне перетворення продукту в результати тимчасової області в Y_W$(c,\tau )$ для різних дискретних значень τ і дискретне значення $c_{n}$. №Повертаємося до другого кроку, до тих пір, поки всі значення дискретного масштабування для $c_{n}$ обробляються.

Є багато різних типів вейвлет-перетворення для конкретних цілей. Див. також: повний список вейвлета пов'язаних перетворень, але загальні з них перераховані нижче: мексиканський капелюх, вейвлет Хаара, Вейвлет, вейвлет Добеші, трикутний імпульс.

Див. також

• Continuous wavelet transform
• Дискретне вейвлет-перетворення
• Complex wavelet transform
• Подвійний вейвлет
• Multiresolution analysis
• MrSID, the image format developed from original wavelet compression research at Los Alamos National Laboratory (LANL).
• ECW (file format), a wavelet-based geospatial image format designed for speed and processing efficiency
• JPEG 2000, вейвлет оснований на стандарті стиснення зображень
• DjVu format uses wavelet-based IW44 algorithm for image compression
• scaleograms, a type of spectrogrm generated using wavelets instead of a short-time Fourier transformтип спектрограми, яка генерується з використанням вейвлетів, замість віконного перетворення Фур'є.
• Вейвлет Морлета
• Chirplet transform
• Time-frequency representation
• S transform
• Віконне перетворення Фур'є
• Ів Мейєр
• Інгрід Добеші
• Стефан Маллат
• Вейвлет Габора

Література

• Вейвлет-перетворення у компресії та попередній обробці зображень / О. В. Капшій, О. І. Коваль, Б. П. Русин ; НАН України, Фіз.-мех. ін-т ім. Г. В. Карпенка. − Л. : Сполом, 2008. − 208 с. : іл. − Бібліогр. : с. 187−203 (238 назв). − ISBN 978-966-665-554-0.