Куб Гільберта

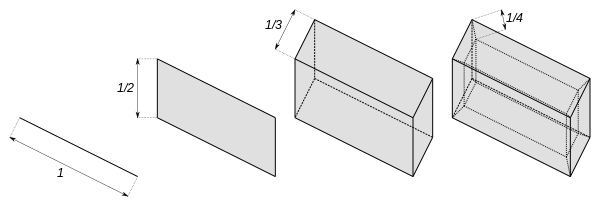
У математиці куб Гільберта названий на честь Девіда Гільберта, — це топологічний простір, який служить повчальним прикладом деяких ідей у топології. Крім того, багато цікавих топологічних просторів можна вкласти в куб Гільберта; тобто їх можна розглядати як підпростори куба Гільберта (див. нижче).

Означення

Куб Гільберта найкраще визначити як топологічний добуток інтервалів $[0,1/n]$ для $n=1,2,3,4,\dots$.

Тобто це кубоїд зліченної нескінченної розмірності, де довжини ребер у кожному ортогональному напрямку утворюють послідовність $\{1/n\}_{n\in \mathbb {N} }$.

Куб Гільберта гомеоморфний добутку зліченної нескінченної кількості копій одиничного інтервалу $[0,1]$.

Іншими словами, його топологічно не можна відрізнити від одиничного куба зліченної нескінченної розмірності.

Якщо точка в кубі Гільберта задана послідовністю $\{a_{n}\}$ з $0\leq a_{n}\leq 1/n$, тоді гомеоморфізм в нескінченномірний одиничний куб визначається як $h(a)_{n}=n\cdot a_{n}$.

Куб Гільберта як метричний простір

Інколи зручно уявляти куб Гільберта як метричний простір, більш того як певну підмножину сепарабельного гільбертового простору (тобто простір Гільберта зі зліченно нескінченним базисом Гільберта). Для цього краще представляти куб не як добуток копій інтервалів $[0,1]$, а як добуток інтервалів

$[0,1]\times [0,1/2]\times [0,1/3]\times \cdots$;

як зазначено вище, для топологічних властивостей це не має значення. Тобто елемент куба Гільберта є нескінченною послідовністю ${x_{n}}$, частини якої задовільняють нерівність $0\leq x_{n}\leq 1/n$.

Будь-яка така послідовність належить гільбертовому простору $\ell _{2}$, тому куб Гільберта наслідує метрику звідти. Можна показати, що топологія, яка індукована метрикою, є такою ж, як топологія добутку у наведеному вище означенні.

Властивості

Як продукт компактних гаусдорфових просторів, куб Гільберта сам є компактним гаусдорфовим простором відповідно до теореми Тихонова. Компактність куба Гільберта також можна довести без аксіоми вибору, побудувавши неперервну функцію зі звичайної множини Кантора в куб Гільберта.

У $\ell _{2}$ жодна точка не має компактного околу (отже, $\ell _{2}$ не є локально компактним). Можна очікувати, що всі компактні підмножини простору $\ell _{2}$ є скінченновимірними, однак куб Гільберта показує, що це не так. Адже він не може бути околом деякої точки $p$, оскільки його сторона стає все меншою і меншою зі збільшенням розмірності і відкрита куля навколо точки $p$ будь-якого фіксованого радіуса $\varepsilon >0$ повинна виходити за межі куба у деякій розмірності.

Будь-яка нескінченновимірна опукла компактна підмножина простору $\ell _{2}$ гомеоморфна кубу Гільберта. Куб Гільберта — це опукла множина, лінійною оболонкою якої є весь простір, проте внутрішня частина пуста множина. Така ситуація неможлива в скінченних розмірностях. Дотичним конусом до куба у нуль-векторі є весь простір.

Кожна підмножина куба Гільберта успадковує від нього властивість метричності (і, отже, аксіому T4) і другу аксіому зліченності. Більш цікаво, що має місце і зворотне: будь-який простір, що задовольняє другу аксіому зліченності і аксіому T4 гомеоморфний підмножині куба Гільберта.

Будь-яка ${G_{\delta }}$-підмножина куба Гільберта є польським простором, тобто топологічним простором, що гомеоморфний сепарабельному та повному метричному простору. І навпаки, будь-який польський простір гомеоморфний ${G_{\delta }}$-підмножині куба Гільберта.

Література

• Srivastava, Shashi Mohan (1998). A Course on Borel Sets. Graduate Texts in Mathematics. Springer-Verlag. ISBN 978-0-387-98412-4. Процитовано 4 грудня 2008.
• Die Homoiomorphie der kompakten konvexen Mengen im Hilbertschen Raum [The homomorphism of the compact convex sets in Hilbert space] (нім.). EUDML. Архів оригіналу за 2 березня 2020.

Додаткова література

• Steen, Lynn Arthur; Seebach, J. Arthur Jr. (1995). Counterexamples in Topology (вид. Dover reprint of 1978). Berlin, New York: Springer-Verlag. ISBN 978-0-486-68735-3. MR 0507446.