Діаграми Коксетера — Динкіна

Діаграми Коксетера — Динкіна для фундаментальних скінченних груп Коксетера

Діаграми Коксетера — Динкіна для фундаментальних афінних груп Коксетера

В геометрії діаграма Коксетера — Динкіна (або діаграма Коксетера, граф Коксетера, схема Коксетера) — це граф з позначеними числами ребрами (так званими гілками), що представляють просторові зв'язки між набором дзеркальних симетрій (або гіперплощин дзеркальних відображень). Діаграма описує калейдоскопічну побудову — кожна «вершина» графу це дзеркало (грань фундаментальної області), а мітки гілок задають величину двогранного кута між двома дзеркалами (на гребені фундаментальної області, тобто на межі з розмірністю $n-2$). Непомічені гілки неявно припускають ступінь 3.Кожна діаграма — це група Коксетера.

Діаграми Динкіна тісно пов'язані з діаграмами Коксетера і відрізняються від них тим, що:

по-перше, гілки з міткою «4» і вище є орієнтованими, в той час як в діаграмах Коксетера — неорієнтовані;

по-друге, діаграми Динкіна повинні задовольняти додатковому (кристалографічному) обмеженню, а саме, мітки дозволені тільки 2, 3, 4 і 6. Діаграми Динкіна відповідають системі коренів і використовуються для їх класифікації, тому відповідають напівпростим групам Лі.

Опис

Гілки діаграми Коксетера — Динкіна позначаються раціональними числами p, відповідними двогранним кутами 180° / p. Якщо p = 2, кут дорівнює 90° і дзеркала не впливають одне на одного, гілка може бути виключена з діаграми. Якщо гілка не позначена, домовляються, що p = 3, що відповідає куту 60°. Два паралельних дзеркала мають гілку, позначену знаком «∞». У загальному випадку, n відображень можуть бути представлені повним графом, в якому всі n(n − 1) / 2 гілок намальовані. На практиці, майже всі цікаві комбінації відображень містять деяку кількість прямих кутів, так що відповідні гілки можуть бути виключені.

Діаграми можуть бути позначені відповідно до структури графу. Першими формами, які вивчав Людвіг Шлефлі, були симплекси, що визначаються сукупністю взаємнопенпердикулярних ребер. Ці симплекси Шлефлі назвав ортосхемами. Ортосхеми виникають в різних ситуаціях, особливо при розгляді правильних політопів і правильних стільників. Плагіосхеми — це симплекси, представлені розгалуженими графами, а циклосхеми — симплекси, представлені циклічними графами.

Матриця Грама (Шлефлі)

Будь-яка діаграма Коксетера має відповідну матрицю Шлефлі з елементами $a_{i,\;j}=a_{j,\;i}=-2\cos \left({\frac {\pi }{p}}\right)$, де $p$ — порядок гілки між парами віддзеркалень. Як матриця косинусів, вона також називається матрицею Грама. Всі матриці Грама групи Коксетера симетричні, оскільки їх кореневі вектора нормалізовані. Вони близько пов'язані з матрицями Картана, які використовуються у схожому контексті, але для орієнтованих графів діаграм Динкіна для випадків p = 2,3,4 і 6, в загальному випадку, НЕ симетричні.

Визначник матриці Шлефлі називається шлефіаном (він же граміан), його знак визначає, чи є група скінченною (додатний визначник), афінною (нульовий) або невизначеною (від'ємний). Це правило називається критерієм Шлефлі.

Власні значення матриці Грама визначають, чи є група Коксетера скінченного типу (всі значення додатні), афінного типу (всі невід'ємні, щонайменше одне значення дорівнює нулю) або невизначеного типу (всі інші випадки). Невизначений тип іноді розбивається на підтипи, наприклад, на гіперболічні й інші групи Коксетера. Однак є багато не еквівалентних визначень гіперболічних груп Коксетера. Ми використовуємо наступне визначення: Група Коксетера з відповідною діаграмою є гіперболічною, якщо вона ні скінченного, ні афінного типів, але будь-яка зв'язкова піддіаграма має або скінченний, або афінний тип. Гіперболічна група Коксетера компактна, якщо всі її підгрупи скінченні (тобто мають додатні визначники) і паракомпактна, якщо всі її підгрупи скінченні або афінні (тобто мають невід'ємні визначники).

Скінченні і афінні групи також називаються еліптичними і параболічними відповідно. Гіперболічні групи називаються також групами Ланнера, який перерахував компактні гіперболічні групи в 1950-м, а паракомпактні групи — групами Козуля (або квазіланнеровими групами). Зустрічаються й інші назви. Так, в статті Максвелла скінченні групи називаються додатними, а афінні — евклідові.

Групи Коксетера рангу 2

Для рангу 2 тип групи Коксетера повністю визначений визначником матриці Грама, оскільки він просто дорівнює добутку його власних значень: скінченний тип (додатний визначник), афінний тип (нульовий визначник) або гіперболічний тип (від'ємний визначник). Коксетер використовує еквівалентну дужкову нотацію, яка перераховує послідовності порядків гілок замість графічних діаграм вузол-гілка.

Тип	Скінченна					Афінна	Гіперболічна
Геометрія					…
Коксетер	[ ]	[2]	[3]	[4]	[p]	[∞]	[∞]	[iπ/λ]
степінь	2	4	6	8	2p	∞
Прямі відображення розфарбовані відповідно вузлів діаграми Коксетера. Фундаментальні області пофарбовані в альтернативні кольори.

Діаграми групи Коксетера рангу 2

степінь p	Група	Діаграма Коксетера		Матриця Грама
				$\left[{\begin{matrix}2&a_{12}\\a_{21}&2\end{matrix}}\right]$	Визначник (4-a21*a12)
Скінченна (Визначник>0)
2	I2(2) = A1xA1		[2]	$\left[{\begin{smallmatrix}2&0\\0&2\end{smallmatrix}}\right]$	4
3	I2(3) = A2		[3]	$\left[{\begin{smallmatrix}2&-1\\-1&2\end{smallmatrix}}\right]$	3
4	I2(4) = B2		[4]	$\left[{\begin{smallmatrix}2&-{\sqrt {2}}\\-{\sqrt {2}}&2\end{smallmatrix}}\right]$	2
5	I2(5) = H2		[5]	$\left[{\begin{smallmatrix}2&-\phi \\-\phi &2\end{smallmatrix}}\right]$	$4\sin ^{2}(\pi /5)$ =$(5-{\sqrt {5}})/2$ ~1.38196601125
6	I2(6) = G2		[6]	$\left[{\begin{smallmatrix}2&-{\sqrt {3}}\\-{\sqrt {3}}&2\end{smallmatrix}}\right]$	1
8	I2(8)		[8]	$\left[{\begin{smallmatrix}2&-2\cos(\pi /8)\\-2\cos(\pi /8)&2\end{smallmatrix}}\right]$	$2-{\sqrt {2}}$ ~0.58578643763
10	I2(10)		[10]	$\left[{\begin{smallmatrix}2&-2\cos(\pi /10)\\-2\cos(\pi /10)&2\end{smallmatrix}}\right]$	$4\sin ^{2}(\pi /10)$ =$(3-{\sqrt {5}})/2$ ~0.38196601125
12	I2(12)		[12]	$\left[{\begin{smallmatrix}2&-2\cos(\pi /12)\\-2\cos(\pi /12)&2\end{smallmatrix}}\right]$	$2-{\sqrt {3}}$ ~0.26794919243
p	I2(p)		[p]	$\left[{\begin{smallmatrix}2&-2\cos(\pi /p)\\-2\cos(\pi /p)&2\end{smallmatrix}}\right]$	$4\sin ^{2}(\pi /p)$
Афінна (Визначник=0)
∞	I2(∞) = ${\tilde {I}}_{1}$ = ${\tilde {A}}_{1}$		[∞]	$\left[{\begin{smallmatrix}2&-2\\-2&2\end{smallmatrix}}\right]$	0
Гіперболічна (Визначник≤0)
∞			[∞]	$\left[{\begin{smallmatrix}2&-2\\-2&2\end{smallmatrix}}\right]$	0
∞			[iπ/λ]	$\left[{\begin{smallmatrix}2&-2cosh(2\lambda )\\-2cosh(2\lambda )&2\end{smallmatrix}}\right]$	$-4\sinh ^{2}(2\lambda )\leq 0$

Геометричне уявлення

Діаграму Коксетера — Динкіна можна розглядати як графічний описфундаментальної області відображень. Дзеркалом (безліччю нерухомих точок відображення) є гіперплощина в заданому сферичному, евклідовому або гіперболічному просторі. (У двовимірному просторі дзеркалом є пряма, а в тривимірному — площина).

Нижче показані фундаментальні області двовимірних і тривимірних евклідових груп, а також двовимірних сферичних груп. Для кожної групи діаграма Коксетера може бути виведена шляхом визначення гіперплощин і розмітки їх зв'язків, ігноруючи двогранні кути в 90 градусів (порядок 2).

Група Коксетера	${\tilde {C}}_{2}$	${\tilde {I}}_{1}$x${\tilde {I}}_{1}$	${\tilde {G}}_{2}$	${\tilde {A}}_{2}$
	[4,4]	[∞4,∞]	[6,3]	[(3,3,3)] = [3[3]]
Фундаментальна область
Диаграма Коксетера — Динкіна

Групи Коксетера на евклідовій площині з відповідними діаграмами. Дзеркала позначені як вузли графу R1, R2, і т. д. та розфарбовані відповідно до порядку відображення. Відображення на 90 градусів нічого не змінюють, а тому видалені з діаграми. Паралельні відображення відзначені символом ∞. Призматична група ${\tilde {I}}_{1}$x${\tilde {I}}_{1}$ зображена як подвоєння ${\tilde {C}}_{2}$, але вона також може бути створена як прямокутні області, отримані з подвоєння трикутників ${\tilde {G}}_{2}$. ${\tilde {A}}_{2}$ є подвоєнням трикутника ${\tilde {G}}_{2}$.

Деякі гіперболічні калейдоскопи

Група Коксетера	[n,4]	[∞n,∞]	[n,3]	[(n,3,3)]
Фундаментальна область
Двоїстий граф (повна схема Коксетера)
Диаграма Коксетера — Динкіна
	n=5,6…	n=3,4…	n=7,8…	n=4,5

Багато груп Коксетера нагіперболічній площині можуть бути поширені з евклідового випадку як серії гіперболічних рішень.

Групи Коксетера в тривимірному просторі з відповідними діаграмами. Дзеркала (трикутні грані) позначені протилежними вершинами 0..3. Гілки пофарбовані відповідно до порядку відображень. ${\tilde {C}}_{3}$ заповнює 1/48 частин куба. ${\tilde {B}}_{3}$ заповнює 1/24 частин куба. ${\tilde {A}}_{3}$ заповнює 1/12 частин куба.

Групи Коксетера на сфері з відповідними діаграмами. Одна фундаментальна область виділена жовтим кольором. Вершини області (і гілки графу) пофарбовані відповідно до порядку відображення.

Скінченні групи Коксетера

Див. також сімейства багатогранників для таблиці однорідних багатогранників, пов'язаних з цими групами.

• Для кожної групи наведені три різних позначення — буквено-цифрове позначення, набір цифр в дужках і діаграма Коксетера.
• Розгалужені групи D_n є половинними або знакозмінними версіями звичайних груп C_n.
• Для розгалужених груп D_n і E_n наведені позначення з верхніми індексами [3^a,b,c], де числа a,b і c задають кількість сегментів у кожній з трьох гілок.

Зв'язані графи Динкіна з рангами від 1 до 9

Ранг	Прості групи Лі			Виключні групи Лі
	${A}_{1+}$	${BC}_{2+}$	${D}_{2+}$	${E}_{3-8}$	${F}_{3-4}$	${G}_{2}$	${H}_{2-4}$	${I}_{2}(p)$
1	A1=[]
2	A2=[3]	B2=[4]	D2=A1xA1			G2=[6]	H2=[5]	I2[p]
3	A3=[32]	B3=[3,4]	D3=A3	E3=A2A1	F3=B3		H3
4	A4=[33]	B4=[32,4]	D4=[31,1,1]	E4=A4	F4		H4
5	A5=[34]	B5=[33,4]	D5=[32,1,1]	E5=D5
6	A6=[35]	B6=[34,4]	D6=[33,1,1]	E6=[32,2,1]
7	A7=[36]	B7=[35,4]	D7=[34,1,1]	E7=[33,2,1]
8	A8=[37]	B8=[36,4]	D8=[35,1,1]	E8=[34,2,1]
9	A9=[38]	B9=[37,4]	D9=[36,1,1]
10+	..	..	..	..

Застосування до однорідних політопів

При побудові однорідних багатогранників вузли маркуються як активні шляхом додавання кола, якщо генеруюча точка знаходиться поза дзеркалом (гіперплощини, щодо якої проводиться відображення), тим самим утворюючи нове ребро між генеруючою точкою та її відображенням. Вузли без кола це неактивні відображення, які не генерують нових точок.

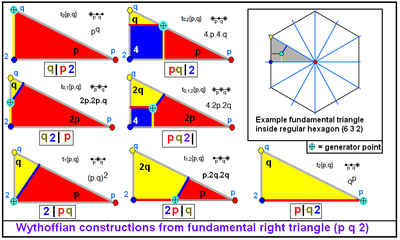
Діаграми Коксетера — Динкіна можуть перерахувати майже всі класи однорідних багатогранників та однорідних мозаїк. Кожен однорідний багатогранник з простою дзеркальною симетрією (всі вони, за винятком декількох спеціальних випадків, мають просту дзеркальну симетрію) можуть бути представлені діаграмами Коксетера — Динкіна з перестановками міток. Кожен однорідний багатогранник можна отримати, використовуючи такі дзеркала й одну генеруючу точку — відображення створюють у результаті симетрії нової точки, потім можна визначити ребра багатогранника між точками і їх дзеркальними відображеннями. Грані можна побудувати при отриманні циклу з ребер і т. д. Для завдання генеруючої вершини один або більше вузлів позначаються колами, що означає, що вершина не знаходиться на дзеркалі, представлених поміченими колами вузлами. (Якщо два або більше дзеркала позначені, вершина розташовується на рівновіддалених відстані від них.) Дзеркало активно (створює відображення), тільки для точок, які не лежать на ньому. Діаграма повинна мати щонайменше один активний вузол для подання багатогранника.

Усі правильні багатовимірні багатогранники, представлені символом Шлефлі ((p, q, r, …), можуть мати фундаментальні області, представлені набором n дзеркал з відповідною діаграмою Коксетера -Динкіна у вигляді послідовності вузлів і гілок, помічених p, q, r, … з першим обведеним колом вузлом.

Однорідні багатогранники з одним колом відповідають генеруючим точкам у кутах симплекса фундаментальної області. Два гуртка відповідають ребрам симплекса й мають свободу вибору, але тільки середина призводить до однорідного рішенням з однаковими довжинами ребер. У загальному випадку генератори з k-колами є (k-1)-вимірним гранями симплекса. Якщо всі вузли позначені колами, генеруюча точка знаходиться всередині симплекса.

Інший елемент розмітки висловлює спеціальний випадок недзеркальної симетрії однорідних багатогранників. Ці випадки існують як альтернації дзеркальної симетрії багатогранників. У цьому елементі розмітки відсутня центральна точка позначеного колом вузла, який тоді називається діркою, і означає такий вузол віддалену альтернуючу вершину. Отриманий багатогранник матиме підсімметрії вихідної групи Коксетера. Усічена альтернація називається відрізком.

• Окремий вузол це окреме дзеркало. Відповідна група позначається A₁. Коло навколо вузла призводить до утворення відрізка, перпендикулярного дзеркала, і він позначається як {}.
• Два незв'язаних вузла представляють два перпендикулярних дзеркала. Якщо обидва вузла обведені колом, може бути створений прямокутник, або квадрат, якщо точки розташовані на однаковій відстані від обох дзеркал.
• Два вузла, з'єднаних гілкою порядку n, можуть створити n — кутник, якщо точка знаходиться на одному з дзеркал, і 2n  — кутник, якщо крапка не лежить ні на одному з дзеркал. Ці два вузла утворюють групу I₁(n).
• Два паралельних дзеркала можуть представляти групу нескінченного багатокутника I₁(∞), що позначається також Ĩ₁.
• Три дзеркала у вигляді трикутника утворюють образи, які спостерігаються в традиційному калейдоскопі і така конфігурація може бути представлена ​​трьома вузлами, з'єднаними в трикутник. Періодичні приклади матимуть гілки, помічені як (3 3 3), (2 4 4) і (2 3 6), хоча останні два можуть побут намальовані як прямі (видаливши гілки 2). Вони генерують однорідні мозаїки.
• Три дзеркала можуть створити однорідний багатогранник, наприклад, трикутники Шварца, одержувані з раціональних чисел.
• Три дзеркала, де одне дзеркало перпендикулярно двом іншим, можуть створити однорідні призми.

Є 7 дзеркальних однорідних конструкцій для загального трикутника, заснованих на 7 топологічних позиціях генератора всередині фундаментальної області. Будь-яке одиничне активне дзеркало має генератор в куті та утворює ребро, для двох дзеркал генератор знаходиться на одній зі сторін трикутника, а три активних дзеркала мають генератор всередині трикутника. Один або два ступені свободи можна звести до однієї позиції для досягнення однакових довжин ребер результуючого багатогранника або мозаїки.

Приклад семи генераторів при октаедричної симетрії з фундаментальним трикутником (4 3 2) і восьмим генератором обрізка

Подвійні однорідні багатогранники іноді позначаються вертикальними рисками замість позначених кіл вузлів, а перекреслений порожній вузол (без внутрішньої точки) означає відсікання. Наприклад, представляє прямокутник (як два активних ортогональних дзеркала), а представляє його двоїстий багатокутник (ромб).

Приклади багатогранників і мозаїк

Як приклад група Коксетера B ₃ має схему . Вона також називається октаедричною симетрією.

Є 7 опуклих однорідних багатогранників, які можна побудувати за допомогою цієї групи симетрії та 3 з її альтернаційних підсиметрій, кожна з єдиною схемою Коксетера — Динкіна. Символ Вітгофа це спеціальний випадок схеми Коксетера для графів рангу 3 з усіма трьома гілками без видалення гілок порядку 2. Символ Вітгофа здатний працювати з обрізками, але не з загальними альтернаціями, коли не всі вузли позначені колами.

Однорідні октаедричні багатогранники

Симетрії: [4,3], *432							[4,3]+, (432)	[3+,4], (3*2)
{4,3}	t{4,3}	r{4,3}	t{3,4}	{3,4}	rr{4,3}	tr{4,3}	sr{4,3}	s{3,4}
Двоїсті багатогранники
V43	V3.82	V(3.4)2	V4.62	V34	V3.43	V4.6.8	V34.4	V35

Ті ж побудови можна виконати з незв'язними (ортогональними) групами Коксетера, на зразок групи однорідних призм, і можуть розглядатися з більшою ясністю як мозаїки діедр і осоедр на сфері, на зразок сімейств [6]×[] або [6,2]:

Однорідні шестикутні діедричні сферичні багатогранники

Симетрія|: [6,2], (*622)							[6,2]+, (622)	[6,2+], (2*3)
{6,2}	t{6,2}	r{6,2}	t{2,6}	{2,6}	rr{2,6}	tr{6,2}	sr{6,2}	s{2,6}
Двоякі їм багатогранники
V62	V122	V62	V4.4.6	V26	V4.4.6	V4.4.12	V3.3.3.6	V3.3.3.3

У порівнянні з [6,3], сімейство породжує два паралельних сімейства 7 однорідних мозаїк евклідової площини і їх двоїстих мозаїк. Знову маємо 3 альтернації і кілька напівсиметричних версій.

Є вісім однорідних мозаїк, які базуються на правильних шестикутних мозаїках (або подвійних трикутних мозаїках). Якщо намалювати мозаїку, розмальовуючи елементи мозаїки в червоний для граней, в жовтий для вершин і в блакитний для ребер, отримаємо 8 видів мозаїки, 7 з яких топологічно різні. Усічена трикутна мозаїка топологічно ідентична шестикутній.

Однорідні шестикутні/трикутні мозаїки]]

Симетрія: [6,3], (*632)							[6,3]+ (632)	[6,3+] (3*3)
{6,3}	t{6,3}	r{6,3}	t{3,6}	{3,6}	rr{6,3}	tr{6,3}	sr{6,3}	s{3,6}
63	3.122	(3.6)2	6.6.6	36	3.4.12.4	4.6.12	3.3.3.3.6	3.3.3.3.3.3
Двоякі їм однорідні мозаїки
V63	V3.122	V(3.6)2	V63	V36	V3.4.12.4	V.4.6.12	V34.6	V36

На гіперболічній площині [7,3] сімейство породжує дві паралельні множини однорідних мозаїк евклідової площині і двоїстих їм мозаїк. Є тільки одна альтернація (обрізок), оскільки всі гілки непарні. Багато інших гіперболічних сімейств однорідних мозаїк можна побачити серед однорідних мозаїк на гіперболічної площині.

Однорідні семикутні/трикутні мозаїки

Симетрія: [7,3], (*732)							[7,3]+, (732)
{7,3}	t{7,3}	r{7,3}	2t{7,3}=t{3,7}	2r{7,3}={3,7}	rr{7,3}	tr{7,3}	sr{7,3}
Однорідні двоїсті мозаїки
V73	V3.14.14	V3.7.3.7	V6.6.7	V37	V3.4.7.4	V4.6.14	V3.3.3.3.7

Афінні групи Коксетера

Сімейства опуклих однорідних евклідових мозаїк визначаються афінною групою Коксетера. Ці групи ідентичні скінченним групам з додаванням одного вузла. У літерних позначеннях у них та ж буква, що і у тильди, знак «~» над буквою. Індекс стосується скінченної групи, так що ранг дорівнює індексу + 1. (Символи Вітта для афінних груп дані з позначкою також)

1. ${\tilde {A}}_{n-1}$: діаграми цього типа це цикли. (Також P_n)
2. ${\tilde {C}}_{n-1}$ асоційована з родиною гіперкубічних правильних мозаїк||hypercubic honeycomb}} (3, …., 4). (Також R_n)
3. ${\tilde {B}}_{n-1}$ зв'язана з С видаленням одного мінору.(Також S_n)
4. ${\tilde {D}}_{n-1}$ зв'язана з С видаленням двох мінорів. (Також Q_n)
5. ${\tilde {E}}_{6}$, ${\tilde {E}}_{7}$, ${\tilde {E}}_{8}$. (Також T₇, T₈, T₉)
6. ${\tilde {F}}_{4}$ утворює {3,4,3,3} правильну мозаїку. (Також U₅)
7. ${\tilde {G}}_{2}$ утворює 30-60-90 трикутні фундаментальні області. (Також V₃)
8. ${\tilde {I}}_{1}$ складається з двох паралельних дзеркал. (= ${\tilde {A}}_{1}$ = ${\tilde {C}}_{1}$) (Also W₂)

Складові групи можна визначити як ортогональні системи. Найбільш часто використовується${\tilde {A}}_{1}$. Таким чином, наприклад, ${\tilde {A}}_{1}^{2}$ представляє квадратні або прямокутні області на евклідовій площині, а ${\tilde {A}}_{1}{\tilde {G}}_{2}$ представляє фундаментальну область у вигляді трикутної призми в евклідовому тривимірному просторі.

Афінні групи Коксетера (від 2 до 10 вузлів)

Ранг	${\tilde {A}}_{1+}$ (P2+)	${\tilde {B}}_{3+}$ (S4+)	${\tilde {C}}_{1+}$ (R2+)	${\tilde {D}}_{4+}$ (Q5+)	${\tilde {E}}_{n}$ (Tn+1) / ${\tilde {F}}_{4}$ (U5) / ${\tilde {G}}_{2}$ (V3)
2	${\tilde {A}}_{1}$=[∞]		${\tilde {C}}_{1}$=[∞]
3	${\tilde {A}}_{2}$=[3[3]] *		${\tilde {C}}_{2}$=[4,4] *		${\tilde {G}}_{2}$=[6,3] *
4	${\tilde {A}}_{3}$=[3[4]] *	${\tilde {B}}_{3}$=[4,31,1] *	${\tilde {C}}_{3}$=[4,3,4] *	${\tilde {D}}_{3}$=[31,1,3−1,31,1] = ${\tilde {A}}_{3}$
5	${\tilde {A}}_{4}$=[3[5]] *	${\tilde {B}}_{4}$=[4,3,31,1] *	${\tilde {C}}_{4}$=[4,32,4] *	${\tilde {D}}_{4}$=[31,1,1,1] *	${\tilde {F}}_{4}$=[3,4,3,3] *
6	${\tilde {A}}_{5}$=[3[6]] *	${\tilde {B}}_{5}$=[4,32,31,1] *	${\tilde {C}}_{5}$=[4,33,4] *	${\tilde {D}}_{5}$=[31,1,3,31,1] *
7	${\tilde {A}}_{6}$=[3[7]] *	${\tilde {B}}_{6}$=[4,33,31,1]	${\tilde {C}}_{6}$=[4,34,4]	${\tilde {D}}_{6}$=[31,1,32,31,1]	${\tilde {E}}_{6}$=[32,2,2]
8	${\tilde {A}}_{7}$=[3[8]] *	${\tilde {B}}_{7}$=[4,34,31,1] *	${\tilde {C}}_{7}$=[4,35,4]	${\tilde {D}}_{7}$=[31,1,33,31,1] *	${\tilde {E}}_{7}$=[33,3,1] *
9	${\tilde {A}}_{8}$=[3[9]] *	${\tilde {B}}_{8}$=[4,35,31,1]	${\tilde {C}}_{8}$=[4,36,4]	${\tilde {D}}_{8}$=[31,1,34,31,1]	${\tilde {E}}_{8}$=[35,2,1] *
10	${\tilde {A}}_{9}$=[3[10]] *	${\tilde {B}}_{9}$=[4,36,31,1]	${\tilde {C}}_{9}$=[4,37,4]	${\tilde {D}}_{9}$=[31,1,35,31,1]
11	…	…	…	…

Гіперболічні групи Коксетера

Є нескінченно багато нескінченних гіперболічних груп Коксетера. Гіперболічні групи діляться на компактні й некомпактні, де компактні групи мають обмежені фундаментальні області. Компактні групи гіперболічних симплексів (симплекси Ланнера) існують для рангів від 3 до 5. Паракомпланарні групи симплексів (симплекси Козуля) існують аж до рангу 10. Гіперкомпланарні (багатогранники Вінберга) групи досліджувалися, але повністю ще не вивчені. У 2006 Алкок (Allcock) довів, що є нескінченно компактних багатогранників Винберга для просторів розмірності аж до 6 і нескінченно багато багатогранників Вінберга для розмірностей аж до 19, так що повне перерахування неможливо. Всі ці фундаментальні області відображень, як симплексів, так і не симплексів, часто називають політопами Коксетера, або, іноді, що менш точно, багатогранниками Коксетера .

Гіперболічні групи Коксетера в H²

Модель Пуанкаре фундаментальної області трикутників

Приклади прямокутних трикутників [p, q]
[3,7]	[3,8]	[3,9]	[3,∞]
[4,5]	[4,6]	[4,7]	[4,8]	[∞,4]
[5,5]	[5,6]	[5,7]	[6,6]	[∞,∞]
Приклади трикутників загального виду [(p, q, r)]
[(3,3,4)]	[(3,3,5)]	[(3,3,6)]	[(3,3,7)]	[(3,3,∞)]
[(3,4,4)]	[(3,6,6)]	[(3,∞,∞)]	[(6,6,6)]	[(∞,∞,∞)]

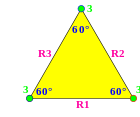
Двовимірні гіперболічні групи трикутників це схеми Коксетера рангу 3, визначині трикутником (p q r):

${\frac {1}{p}}+{\frac {1}{q}}+{\frac {1}{r}}<1.$

Існує нескінченно багато компактних трикутних гіперболічних груп Коксетера, включаючи лінійні і трикутні графи. Лінійні графи існують для прямокутних трикутників (з r = 2).

Компактні гіперболічні групи Коксетера

Лінійні	Циклічні
Регулярні гіперболічні мозайки|∞| [p, q], : 2(p+q)<pq … … …	∞ [(p, q, r)], : p+q+r>9 …

Паракомпактні групи Коксетера рангу 3 існують як межі компактних.

Лінійні графи	Циклічні графи
[p,∞] [∞,∞]	[(p, q,∞)] [(p,∞,∞)] [(∞,∞,∞)]

Скінченною підмножиною гіперболічних груп трикутників є арифметичні групи. Повний список таких груп знайшов за допомогою комп'ютера Кісао Такеучі (Kisao Takeuchi) й опублікував у статті «Арифметичні групи трикутників» у 1977 році. Таких груп 85, з них 76 компактних і 9 паракомпактних.

Прямокутні трикутники (p q 2)	Трикутники загального виду (p q r)
Компактні групи: (76) , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , Паракомпактні прямокутні трикутники: (4) , , ,	Трикутники загального виду: (39) , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , Паракомпактні трикутники загального виду: (5) , , , ,
(2 3 7), (2 3 8), (2 3 9), (2 3 10), (2 3 11), (2 3 12), (2 3 14), (2 3 16), (2 3 18), (2 3 24), (2 3 30): (2 4 5), (2 4 6), (2 4 7), (2 4 8), (2 4 10), (2 4 12), (2 4 18), (2 5 5), (2 5 6), (2 5 8), (2 5 10), (2 5 20), (2 5 30): (2 6 6), (2 6 8), (2 6 12): (2 7 7), (2 7 14), (2 8 8), (2 8 16), (2 9 18): (2 10 10) (2 12 12) (2 12 24), (2 15 30), (2 18 18): (2 3 ∞) (2,4 ∞) (2,6 ∞) (2 ∞ ∞)	(3 3 4), (3 3 5), (3 3 6), (3 3 7), (3 3 8), (3 3 9), (3 3 12), (3 3 15): (3 4 4), (3 4 6), (3 4 12), (3 5 5), (3 6 6), (3 6 18), (3 8 8), (3 8 24), (3 10 30), (3 12 12): (4 4 4), (4 4 5), (4 4 6), (4 4 9), (4 5 5), (4 6 6), (4 8 8), (4 16 16): (5 5 5), (5 5 10), (5 5 15), (5 10 10): (6 6 6), (6 12 12), (6 24 24): (7 7 7) (8 8 8) (9 9 9) (9 18 18) (12 12 12) (15 15 15): (3,3 ∞) (3 ∞ ∞): (4,4 ∞) (6 6 ∞) (∞ ∞ ∞)

Гіперболічні багатогранники Коксетера над трикутниками

Фундаментальна область груп чотирикутників

or [∞,3,∞] [iπ/λ1,3,iπ/λ2] (*3222)	or [((3,∞,3)),∞] [((3,iπ/λ1,3)), iπ/λ2] (*3322)	or [(3,∞)[2]] [(3,iπ/λ1,3,iπ/λ2)] (*3232)	or [(4,∞)[2]] [(4,iπ/λ1,4,iπ/λ2)] (*4242)	(*3333)
Області з ідеальними вершинами
[iπ/λ1,∞,iπ/λ2] (*∞222)	(*∞∞22)	[(iπ/λ1,∞,iπ/λ2,∞)] (*2∞2∞)	(*∞∞∞∞)	(*4444)

Інші H² гіперболічні калейдоскопи можна побудувати з багатокутників більшого порядку. Подібно групам трикутників ці калейдоскопи можна ідентифікувати циклічною послідовністю порядків перетинів дзеркал навколо фундаментальної області, як (a b c d …), або, еквівалентно, (згідно нотації орбіфолдів) як *abcd…. Діаграми Коксетера — Динкіна для цих багатокутних калейдоскопів можна розглядати як фундаментальну область з виродженим $(n-1)$-вимірним симплексом з циклічним порядком гілок a, b, c …, а $n\cdot (n-3)/2$ гілки, що залишилися, позначають як нескінченні (∞) і уявляють непересічні дзеркала. Єдиним негіперболічним прикладом є симетрія чотирьох дзеркал (в евклідовому просторі) квадрата або прямокутника, , [∞,2,∞] (орбіфолд *2222). Інше уявлення гілок непересічних дзеркал, запропоноване Вінбергом, показує нескінченні гілки точковими або пунктирними лініями, так що діаграми виглядають як з передбачуваними чотирма гілками близько 2 навколо периметра.

Наприклад, чотирикутна область (a b c d) буде мати дві гілки нескінченного порядку, що з'єднують ультрапаралельні дзеркала. Найменший гіперболічний приклад — це , [∞,3,∞] або [iπ/λ₁,3,iπ/λ₂] (орбіфолд *3222), де (λ₁,λ₂) це відстань між ультрапаралельними дзеркалами. Альтернативним виразом є , з трьома гілками стенінью 2, передбачуваними навколо периметра. Подібним же чином (2 3 2 3) (орбіфолд * 3232) можна уявити як і (3 3 3 3), (орбіфолд * 3333) можна уявити як повний граф .

Найвищою квадратною областю (∞ ∞ ∞ ∞) є нескінченний квадрат, представлений повним тетраедральним графом з 4 гілками по периметру як ідеальні вершини, і двома діагональними гілками як нескінченність (показано точковими лініями) для ультрапаралельних дзеркал:.

Компакт (групи симплексів Ланнера)

Компактні гіперболічні групи називаються групами Ланнера, на ім'я Фольке Ланнера, який вивчав їх в 1950. Групи існують тільки для графів рангу 4 і 5. Коксетер вивчав лінійні гіперболічні групи (свого імені) в статті 1954-го року Regular Honeycombs in hyperbolic space (Регулярні стільники в гіперболічному просторі), в якій наведено два раціональних рішення в 4-вимірному гіперболічному просторі: [5/2,5,3,3] = і [5,5/2,5,3] = .

Ранги 4-5

Фундаментальна область будь-якої з двох груп, що розщеплюються [5,3^1,1] і [5,3,3^1,1] є подвоєнням відповідної лінійної групи, [5,3,4] та [5,3,3,4] відповідно. Літерні імена груп дані Джонсоном як розширення символів Вітта.

Компактні гіперболічні групи Коксетера

Розмірність Hd	Ранг	Загальне число	Лінійні	Розщіплювані	Циклічні
H3	4	9	Список правильних багатогранників ${\bar {BH}}_{3}$ = [4,3,5]: ${\bar {K}}_{3}$ = [5,3,5]: ${\bar {J}}_{3}$ = [3,5,3]:	${\bar {DH}}_{3}$ = [5,31,1]:	${\widehat {AB}}_{3}$ = [(33,4)]: ${\widehat {AH}}_{3}$ = [(33,5)]: ${\widehat {BB}}_{3}$ = [(3,4)[2]]: ${\widehat {BH}}_{3}$ = [(3,4,3,5)]: ${\widehat {HH}}_{3}$ = [(3,5)[2]]:
H4	5	5	5-комірковий стільник степеня 5 ${\bar {H}}_{4}$ = [33,5]: ${\bar {BH}}_{4}$ = [4,3,3,5]: ${\bar {K}}_{4}$ = [5,3,3,5]:	${\bar {DH}}_{4}$ = [5,3,31,1]:	${\widehat {AF}}_{4}$ = [(34,4)]:

Паракомпакт (групи симплексів Козуля)

Приклад нескінченнокутової мозаїки 3-го порядку, {∞,3} з одним зеленим нескінченнокутником і його описаним орициклом

Паракомпактні гіперболічні групи Коксетера містять афінні підгрупи і мають симплексні в асимптотиці фундаментальні області. Найвищі паракомпактні гіперболічні групи Коксетера мають ранг 10. Ці групи названі ім'ям французького математика Жана-Луїса Козуля. Вони ж називаються квазіланеровськими групами як розширення компактних груп Ланнера. Повний список груп було знайдено Чейном (M. Chein) за допомогою комп'ютера і опублікований в 1969-му.

Згідно Вінберга, всі, крім восьми, з цих 72 компактних і паракомпактних груп є арифметичними. Дві неарифметичні групи компактні - і . Інші шість неарифметичні групи паракомпактні, з них п'ять груп є 3-вимірними (, , , і ), а одна 5-вимірна ().

Ідеальні симплекси

Ідеальні фундаментальні області , [(∞,∞,∞)] в моделі Пуанкаре

Є 5 гіперболічних груп Коксетера, що утворюють ідеальні симплекси, які мають графи, видалення будь-якої однієї вершини призводить до утворення афінної групи Коксетера. В цьому випадку всі вершини цих ідеальних симплексів знаходяться на нескінченності.

Ранг	Ідеальна група		Афічні підгрупи
3	[(∞,∞,∞)]		[∞]
4	[4[4]]		[4,4]
4	[3[3,3]]		[3[3]]
4	[(3,6)[2]]		[3,6]
6	[(3,3,4)[2]]		[4,3,3,4], [3,4,3,3]	,

Ранги 4-10

Нескінченні евклідові комірки на зразок шестикутного паркету під час правильного масштабування сходяться до однієї ідеальної точки в нескінченності.

Існує 58 паракомпактних гіперболічних груп Коксетера рангами від 4 до 10. Всі 58 груп згруповані в п'ять категорій. Буквені позначення групам дав Джонсон як розширені символи Вітта, для чого він використовував букви PQRSTWUV з афінних символів Вітта і додав букви LMNOXYZ. Над буквами позначень гіперболічних груп присутні надкреслення, або кришечки (для циклічних схем). Дужкова нотація Коксетера це лінеаризоване уявлення групи Коксетера.

Гіперболічні паракомпактні групи

Ранг	Повне число	Групи
4	23	${\widehat {BR}}_{3}$ = [(3,3,4,4)]: ${\widehat {CR}}_{3}$ = [(3,43)]: ${\widehat {RR}}_{3}$ = [4[4]]: ${\widehat {AV}}_{3}$ = [(33,6)]: ${\widehat {BV}}_{3}$ = [(3,4,3,6)]: ${\widehat {HV}}_{3}$ = [(3,5,3,6)]: ${\widehat {VV}}_{3}$ = [(3,6)[2]]:	${\bar {P}}_{3}$ = [3,3[3]]: ${\bar {BP}}_{3}$ = [4,3[3]]: ${\bar {HP}}_{3}$ = [5,3[3]]: ${\bar {VP}}_{3}$ = [6,3[3]]: ${\bar {DV}}_{3}$ = [6,31,1]: ${\bar {O}}_{3}$ = [3,41,1]: ${\bar {M}}_{3}$ = [41,1,1]:	${\bar {R}}_{3}$ = [3,4,4]: ${\bar {N}}_{3}$ = [43]: ${\bar {V}}_{3}$ = [3,3,6]: ${\bar {BV}}_{3}$ = [4,3,6]: ${\bar {HV}}_{3}$ = [5,3,6]: ${\bar {Y}}_{3}$ = [3,6,3]: ${\bar {Z}}_{3}$ = [6,3,6]:	${\bar {DP}}_{3}$ = [3[]x[]]: ${\bar {PP}}_{3}$ = [3[3,3]]:
5	9	${\bar {P}}_{4}$ = [3,3[4]]: ${\bar {BP}}_{4}$ = [4,3[4]]: ${\widehat {FR}}_{4}$ = [(32,4,3,4)]: ${\bar {DP}}_{4}$ = [3[3]x[]]:	${\bar {N}}_{4}$ = [4,3,((4,2,3))]: ${\bar {O}}_{4}$ = [3,4,31,1]: ${\bar {S}}_{4}$ = [4,32,1]:	${\bar {R}}_{4}$ = [(3,4)2]:	${\bar {M}}_{4}$ = [4,31,1,1]:
6	12	${\bar {P}}_{5}$ = [3,3[5]]: ${\widehat {AU}}_{5}$ = [(35,4)]: ${\widehat {AR}}_{5}$ = [(3,3,4)[2]]:	${\bar {S}}_{5}$ = [4,3,32,1]: ${\bar {O}}_{5}$ = [3,4,31,1]: ${\bar {N}}_{5}$ = [3,(3,4)1,1]:	${\bar {U}}_{5}$ = [33,4,3]: ${\bar {X}}_{5}$ = [3,3,4,3,3]: ${\bar {R}}_{5}$ = [3,4,3,3,4]:	${\bar {Q}}_{5}$ = [32,1,1,1]: ${\bar {M}}_{5}$ = [4,3,31,1,1]: ${\bar {L}}_{5}$ = [31,1,1,1,1]:
7	3	${\bar {P}}_{6}$ = [3,3[6]]:	${\bar {Q}}_{6}$ = [31,1,3,32,1]:	${\bar {S}}_{6}$ = [4,32,32,1]:
8	4	${\bar {P}}_{7}$ = [3,3[7]]:	${\bar {Q}}_{7}$ = [31,1,32,32,1]:	${\bar {S}}_{7}$ = [4,33,32,1]:	${\bar {T}}_{7}$ = [33,2,2]:
9	4	${\bar {P}}_{8}$ = [3,3[8]]:	${\bar {Q}}_{8}$ = [31,1,33,32,1]:	${\bar {S}}_{8}$ = [4,34,32,1]:	${\bar {T}}_{8}$ = [34,3,1]:
10	3		${\bar {Q}}_{9}$ = [31,1,34,32,1]:	${\bar {S}}_{9}$ = [4,35,32,1]:	${\bar {T}}_{9}$ = [36,2,1]:

Зв'язки підгруп паракомпактних гіперболічних груп

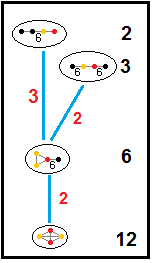
Наведені нижче графи представляють зв'язку підгруп паракомпактних гіперболічних груп. Індекс підгрупи в кожному ребрі заданий червоним кольором. Підгрупи з індексом 2 означають видалення дзеркала й подвоєння фундаментального домену. Інші підгрупи — сумірні (відношення обсягів ціле число).

H3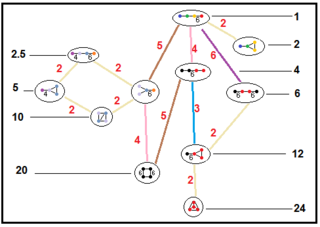
H4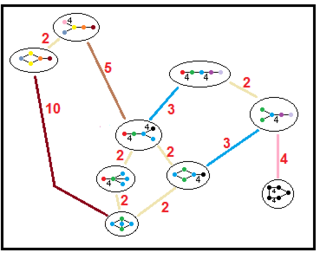
H5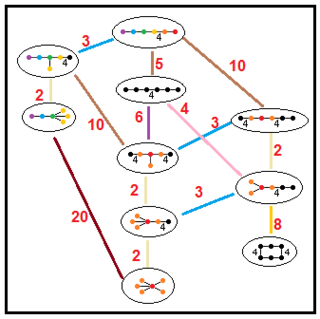

Суперкомпактні групи Коксетера (політопа Вінберга)

Як і для випадку гіперболічної площині H², що має нетрикутні багатокутні фундаментальні області, в більш високих ступенях існують області, які не є симплекс. Ці області можна вважати виродженими симплексами з непересічними дзеркалами, що дають нескінченний порядок.

На схемах Коксетера такі гілки зображаються точковими або пунктирними лініями. Такі області, не є симплексами, називають політопом Вінберга на честь Ернеста Вінберга, який розробив алгоритм для пошуку несимплексної фундаментальної області гіперболічної групи відображень. Геометрично ці фундаментальні області можна класифікувати як чотирикутні піраміди або призми, або інші багатогранники з усіма ребрами, що мають на них двогранні кути π/n для n=2,3,4…

У симплексних областях є n+1 дзеркал для n-вимірного простору. У несимплексних областях є більш ніж n+1 дзеркал. Список скінченний, але повністю ще не відомий. Є часткові списки з n+k дзеркалами для k, рівних 2,3 і 4.

Гіперкомпактні групи Коксетера в тривимірному просторі і вище відрізняються від двовимірних груп в одному відношенні. На площині два гіперболічних n-кутника, мають ті ж самі кути в деякому циклічному порядку, можуть мати різні довжини ребер, і, в загальному випадку, що не конгруентний. Політоп Вінберга в 3-вимірному просторі і вище повністю визначаються двогранними кутами. Цей факт базується на теоремі жорсткості Мостова, яка стверджує, що дві ізоморфні групи, утворені відображеннями в Hⁿ для n>=3, визначають неконгруентні фундаментальні області (політоп Вінберга).

• Повний список політопа Вінберга з рангом дзеркал n + 2 для n-вимірних просторів було видано Ессельманом (F. Esselmann) в 1996.
• Повний список паракомпактних рішень опублікував П. В. Тумаркин в 2003 для розмірностей від 3 до 17.

Найменший паракомпакт вH³ можна уявити як або [∞,3,3,∞], і він може бути побудований шляхом видалення дзеркала з паракомпактної гіперболічної групи [3,4,4]. Подвоєна фундаментальна область перетворюється з тетраедра в чотирикутну піраміду. Інші піраміди включають [4,4,1⁺,4] = [∞,4,4,∞], = . Видалення дзеркала з деяких циклічних гіперболічних графів Коксетера перетворює їх в краватки-метелики: [(3,3,4,1⁺,4)] = [((3,∞,3)), ((3,∞,3))] або , [(3,4,4,1⁺,4)] = [((4,∞,3)), ((3,∞,4))] або , [(4,4,4,1⁺,4)] = [((4,∞,4)), ((4,∞,4))] або .

Інші паракомпактні графи з фундаментальними областями у вигляді чотирикутних пірамід включають:

Розмырнысть	Ранг	Графи
H3	5	, , , , , , , , , , , , , , , , , , , , , , , , , , ,

Ще одна підгрупа [1⁺,4^1,1,1] = [∞,4,1⁺,4,∞] = [∞^[6]]. = = .

Політоп Вінберга рангу n + 3 для n-вимірного простору

Є скінченне число вироджених фундаментальних областей в просторах до 8 розмірностей. Повний список компактних політопів Вінберга з рангом дзеркал n + 3 для n-вимірних просторів дав П. В. Тумаркін в 2004. Ці групи позначені точковими/пунктирними лініями для ультрапаралельних гілок.

Для розмірностей від 4 до 8, число груп Коксетера рангу від 7 до 11 дорівнює 44, 16, 3, 1 і 1 відповідно. Група з великим рангом була відкрита Бугаєнко в 1984 в просторі розмірності 8, і вона має ранг 11:

Dimensions	Rank	Cases	Graphs
H4	7	44	…
H5	8	16	..
H6	9	3
H7	10	1
H8	11	1

Політоп Вінберга рангу n + 4 для n-вимірного простору

Існує за скінченним числом вироджених фундаментальних симплексів в розмірностях аж до восьмої. Компактні політопи Вінберга з рангом дзеркал n + 4 для розмірності n досліджували Анна Феліксон і Павло Тумаркін в 2005.

Групи Лоренца

Правильні стільники з групами Лоренца

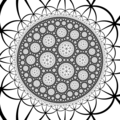Тетраедричний стільник 7-го порядку {3,3,7} в гіперболічному 3-вимірному просторі. Представлений як перетин стільника з площиною на нескінченності в моделі півпростору Пуанкаре.

Семикутний мозаїчний стільник {7,3,3}, представлений поза моделлю кулі Пуанкаре.

Малюнок показує групи Лоренца рангу 5, впорядковані як підгрупи [6,3,3,3] і [6,3,6,3]. Високосиметрична група , [3^[3,3,3]] є підгрупою групи [6,3,3,3] з індексом 120.

Групи Лоренца є групами перетворень Лоренца простору Мінковського. Вони мають зв'язок з геометрією Лоренца, названої ім'ям Хендріка Лоренца, яка застосовується в спеціальній теорії відносності, і з поняттям простору-часу в загальній теорії відносності, що містить часоподібні вектори, скалярний добуток яких на себе дає від'ємне число.

У статті 1982-го року Максвелла Пакування сфер і гіперболічні групи відображень (George Maxwell, Sphere Packings and Hyperbolic Reflection Groups) наведено список груп Лоренца рангів від 5 до 11. Наведений список повний, але не відображає випадки, коли одна група є підгрупою іншої. Є нескінченно багато груп Лоренца з рангом 4. Для рангів 5-11 є скінченне число груп Лоренца — 186, 66, 36, 13, 10, 8 і 4 відповідно. У статті 2013-го Чен і Лаббе (H. Chen, J.-P. Labbé, Lorentzian Coxeter groups and Boyd — Maxwell ball packings) заново перерахували і доповнили список.

Лоренцеві групи Коксетера

Ранг	Загальне число	Групи
4	∞	[3,3,7] … [∞,∞,∞]: … [4,3[3]] … [∞,∞[3]]: … [5,41,1] … [∞1,1,1]: … … [(5,4,3,3)] … [∞[4]]: … … … [4[]×[]] … [∞[]×[]]: … … [4[3,3]] … [∞[3,3]]
5	186	…[3[3,3,3]]: …
6	66
7	36	[31,1,1,1,1,1]: …
8	13	[3,3,3[6]]: [3,3[6],3]: [3,3[2+4],3]: [3,3[1+5],3]: [3[ ]e×[3]]:	[4,3,3,33,1]: [31,1,3,33,1]: [3,(3,3,4)1,1]: [32,1,3,32,1]:		[4,3,3,32,2]: [31,1,3,32,2]:
9	10	[3,3[3+4],3]: [3,3[9]]: [3,3[2+5],3]:	[32,1,32,32,1]:	[33,1,33,4]: [33,1,3,3,31,1]:	[33,3,2]: [32,2,4]: [32,2,33,4]: [32,2,3,3,31,1]:
10	8	[3,3[8],3]: [3,3[3+5],3]: [3,3[9]]:	[32,1,33,32,1]:	[35,3,1]: [33,1,34,4]: [33,1,33,31,1]:	[34,4,1]:
11	4		[32,1,34,32,1]:	[32,1,36,4]: [32,1,35,31,1]:	[37,2,1]:

Дуже розширені діаграми Коксетера

Іноді використовується поняття дуже розширені діаграми Динкіна, в яких афінні групи вважаються розширеними, гіперболічні групи істотно розширеними, а третя гілка — дуже розширеними простими групами. Ці розширення зазвичай позначаються символами 1,2 або 3 + в верхньому індексі для числа розширених вершин. Ці розширені серії можуть бути розширені в зворотньому напрямку шляхом послідовного видалення вузлів у тій самій позиції графу, хоча процес зупиняється після видалення розгалуженого вузла. Розширене сімейство E₈ це найбільш відомий приклад розширення в зворотному напрямку з E₃ і вперед до E₁₁.

Процес розширення може дати обмежені серії графів Коксетера, які проходять шлях від скінченних до афінних, потім до гіперболічних і групам Лоренца. Визначник матриць Картана задає, де серія змінюється від скінченної (додатний визначник) до афінної (нульовий), потім в гіперболічний тип (від'ємний), і завершується групою Лоренца, що містить щонайменше одну гіперболічного підгрупу. Некристалографічні групи H_n утворюють розширену серію, де H₄ розширюється в компактну гіперболічного групу та істотно розширюється в групу Лоренца.

Визначник матриці Шлефлі по рангах:

• det(A₁ⁿ=[2^n-1]) = 2ⁿ (скінченна для всіх n)
• det(A_n=[3^n-1]) = n+1 (скінченна для всіх n)
• det(B_n=[4,3^n-2]) = 2 (скінченна для всіх n)
• det(D_n=[3^n-3,1,1]) = 4 (скінченна для всіх n)

Визначник матриці Шлефлі в виключних серіях:

• det(E_n = [3^n-3,2,1]) = 9-n (скінченна для E₃(=A₂A₁), E₄(=A₄), E₅(=D₅), E₆, E₇ та E₈, афічна для E₉ (${\tilde {E}}_{8}$), гіперболічна для E₁₀)
• det([3^n-4,3,1]) = 2(8-n) (скінченна для n= от 4 до 7, афінна для (${\tilde {E}}_{7}$) та гіперболічна для n=8.)
• det([3^n-4,2,2]) = 3(7-n) (скінченна для n= от 4 до 6, афінна для (${\tilde {E}}_{6}$) та гіперболічна для n=7.)
• det(F_n=[3,4,3^n-3]) = 5-n (скінченна для F₃(=B₃) і F₄, афінна для F₅ (${\tilde {F}}_{4}$), гіперболічна для F₆)
• det(G_n=[6,3^n-2]) = 3-n (скінченна для G₂, афінна для G₃ (${\tilde {G}}_{2}$), гіперболічна для G₄)

Мале розширення серії

	$A_{2}$	$C_{2}$	$G_{2}$	$A_{3}$	$B_{3}$	$C_{3}$	$H_{4}$
Ранг n	[3[3],3n-3]	[4,4,3n-3]	Gn=[6,3n-2]	[3[4],3n-4]	[4,31,n-3]	[4,3,4,3n-4]	Hn=[5,3n-2]
2	[3] A2	[4] C2	[6] G2		[2] A12	[4] C2	[5] H2
3	[3[3]] A2+=${\tilde {A}}_{2}$	[4,4] C2+=${\tilde {C}}_{2}$	[6,3] G2+=${\tilde {G}}_{2}$	[3,3]=A3	[4,3] B3	[4,3] C3	[5,3] H3
4	[3[3],3] A2++=${\bar {P}}_{3}$	[4,4,3] C2++=${\bar {R}}_{3}$	[6,3,3] G2++=${\bar {V}}_{3}$	[3[4]] A3+=${\tilde {A}}_{3}$	[4,31,1] B3+=${\tilde {B}}_{3}$	[4,3,4] C3+=${\tilde {C}}_{3}$	[5,3,3] H4
5	[3[3],3,3] A2+++	[4,4,3,3] C2+++	[6,3,3,3] G2+++	[3[4],3] A3++=${\bar {P}}_{4}$	[4,32,1] B3++=${\bar {S}}_{4}$	[4,3,4,3] C3++=${\bar {R}}_{4}$	[5,33] H5=${\bar {H}}_{4}$
6				[3[4],3,3] A3+++	[4,33,1] B3+++	[4,3,4,3,3] C3+++	[5,34] H6
Det(Mn)	3(3-n)	2(3-n)	3-n	4(4-n)	2(4-n)

Середнє розширення серії

	$A_{4}$	$B_{4}$	$C_{4}$	$D_{4}$	$F_{4}$	$A_{5}$	$B_{5}$	$D_{5}$
Ранг n	[3[5],3n-5]	[4,3,3n-4,1]	[4,3,3,4,3n-5]	[3n-4,1,1,1]	[3,4,3n-3]	[3[6],3n-6]	[4,3,3,3n-5,1]	[31,1,3,3n-5,1]
3		[4,3−1,1] B2A1	[4,3] B3	[3−1,1,1,1] A13	[3,4] B3		[4,3,3] C3
4	[33] A4	[4,3,3] B4	[4,3,3] C4	[30,1,1,1] D4	[3,4,3] F4		[4,3,3,3−1,1] B3A1	[31,1,3,3−1,1] A3A1
5	[3[5]] A4+=${\tilde {A}}_{4}$	[4,3,31,1] B4+=${\tilde {B}}_{4}$	[4,3,3,4] C4+=${\tilde {C}}_{4}$	[31,1,1,1] D4+=${\tilde {D}}_{4}$	[3,4,3,3] F4+=${\tilde {F}}_{4}$	[34] A5	[4,3,3,3,3] B5	[31,1,3,3] D5
6	[3[5],3] A4++=${\bar {P}}_{5}$	[4,3,32,1] B4++=${\bar {S}}_{5}$	[4,3,3,4,3] C4++=${\bar {R}}_{5}$	[32,1,1,1] D4++=${\bar {Q}}_{5}$	[3,4,33] F4++=${\bar {U}}_{5}$	[3[6]] A5+=${\tilde {A}}_{5}$	[4,3,3,31,1] B5+=${\tilde {B}}_{5}$	[31,1,3,31,1] D5+=${\tilde {D}}_{5}$
7	[3[5],3,3] A4+++	[4,3,33,1] B4+++	[4,3,3,4,3,3] C4+++	[33,1,1,1] D4+++	[3,4,34] F4+++	[3[6],3] A5++=${\bar {P}}_{6}$	[4,3,3,32,1] B5++=${\bar {S}}_{6}$	[31,1,3,32,1] D5++=${\bar {Q}}_{6}$
8						[3[6],3,3] A5+++	[4,3,3,33,1] B5+++	[31,1,3,33,1] D5+++
Det(Mn)	5(5-n)	2(5-n)		4(5-n)	5-n	6(6-n)	4(6-n)

Деякі дуже розширенні серії

	$A_{6}$	$B_{6}$	$D_{6}$	$E_{6}$	$A_{7}$	$B_{7}$	$D_{7}$	$E_{7}$	$E_{8}$
Ранг n	[3[7],3n-7]	[4,33,3n-6,1]	[31,1,3,3,3n-6,1]	[3n-5,2,2]	[3[8],3n-8]	[4,34,3n-7,1]	[31,1,3,3,3,3n-7,1]	[3n-5,3,1]	En=[3n-4,2,1]
3									[3−1,2,1] E3=A2A1
4				[3−1,2,2] A22				[3−1,3,1] A3A1	[30,2,1] E4=A4
5		[4,3,3,3,3−1,1] B4A1	[31,1,3,3,3−1,1] D4A1	[30,2,2] A5				[30,3,1] A5	[31,2,1] E5=D5
6	[35] A6	[4,34] B6	[31,1,3,3,3] D6	[31,2,2] E6		[4,3,3,3,3,3−1,1] B5A1	[31,1,3,3,3,3−1,1] D5A1	[31,3,1] D6	[32,2,1] E6 *
7	[3[7]] A6+=${\tilde {A}}_{6}$	[4,33,31,1] B6+=${\tilde {B}}_{6}$	[31,1,3,3,31,1] D6+=${\tilde {D}}_{6}$	[32,2,2] E6+=${\tilde {E}}_{6}$	[36] A7	[4,35] B7	[31,1,3,3,3,30,1] D7	[32,3,1] E7 *	[33,2,1] E7 *
8	[3[7],3] A6++=${\bar {P}}_{7}$	[4,33,32,1] B6++=${\bar {S}}_{7}$	[31,1,3,3,32,1] D6++=${\bar {Q}}_{7}$	[33,2,2] E6++=${\bar {T}}_{7}$	[3[8]] A7+=${\tilde {A}}_{7}$ *	[4,34,31,1] B7+=${\tilde {B}}_{7}$ *	[31,1,3,3,3,31,1] D7+=${\tilde {D}}_{7}$ *	[33,3,1] E7+=${\tilde {E}}_{7}$ *	[34,2,1] E8 *
9	[3[7],3,3] A6+++	[4,33,33,1] B6+++	[31,1,3,3,33,1] D6+++	[34,2,2] E6+++	[3[8],3] A7++=${\bar {P}}_{8}$ *	[4,34,32,1] B7++=${\bar {S}}_{8}$ *	[31,1,3,3,3,32,1] D7++=${\bar {Q}}_{8}$ *	[34,3,1] E7++=${\bar {T}}_{8}$ *	[35,2,1] E9=E8+=${\tilde {E}}_{8}$ *
10					[3[8],3,3] A7+++ *	[4,34,33,1] B7+++ *	[31,1,3,3,3,33,1] D7+++ *	[35,3,1] E7+++ *	[36,2,1] E10=E8++=${\bar {T}}_{9}$ *
11									[37,2,1] E11=E8+++ *
Det(Mn)	7(7-n)	2(7-n)	4(7-n)	3(7-n)	8(8-n)	2(8-n)	4(8-n)	2(8-n)	9-n

Геометричні сувої

Скінченні і нескінченні сувої

φA : AΓ --> AΓ' для скінченних типів
Γ	Γ'	Описані сувої	схеми Коксетера — Динкіна
I2(h)	Γ(h)	Діедрична сувою
Bn	A2n	(I, sn)
	Dn+1, A2n-1	(A3,+/-ε)
F4	E6	(A3,±ε)
H4	E8	(A4,±ε)
H3	D6
H2	A4
G2	A5	(A5,±ε)
	D4	(D4,±ε)
φ: AΓ+ --> AΓ'+ для всіх афінних типів
${\tilde {A}}_{n-1}$	${\tilde {A}}_{kn-1}$	Locally trivial
${\tilde {B}}_{n}$	${\tilde {D}}_{2n+1}$	(I, sn)
	${\tilde {D}}_{n+1}$, ${\tilde {D}}_{2n}$	(A3,±ε)
${\tilde {C}}_{n}$	${\tilde {B}}_{n+1}$, ${\tilde {C}}_{2n}$	(A3,±ε)
	${\tilde {C}}_{2n+1}$	(I, sn)
${\tilde {C}}_{n}$	${\tilde {A}}_{2n+1}$	(I, sn) & (I, s0)
	${\tilde {A}}_{2n}$	(A3,ε) & (I, s0)
	${\tilde {A}}_{2n-1}$	(A3,ε) & (A3,ε')
${\tilde {C}}_{n}$	${\tilde {D}}_{n+2}$	(A3,-ε) & (A3,-ε')
${\tilde {C}}_{2}$	${\tilde {D}}_{5}$	(I, s1)
${\tilde {F}}_{4}$	${\tilde {E}}_{6}$, ${\tilde {E}}_{7}$	(A3,±ε)
${\tilde {G}}_{2}$	${\tilde {D}}_{6}$, ${\tilde {E}}_{7}$	(A5,±ε)
	${\tilde {B}}_{3}$, ${\tilde {F}}_{4}$	(B3,±ε)
	${\tilde {D}}_{4}$, ${\tilde {E}}_{6}$	(D4,±ε)

Схема Коксетера — Динкіна (з простими зв'язками, скінченна, афінна або гіперболічна), що має симетрію (задовольняє одній умові), може бути перетворена за допомогою симетрії в нову, в загальному випадку багатониткову схему, за допомогою процесу, званого «згорткою».

Геометрично це відповідає ортогональним проєкціям однорідних багатогранників і мозаїк. Цікаво, що будь-яка скінченна схема Коксетера — Динкіна з простими зв'язками може бути згорнута в I₂ (h), де h — Число Коксетера, геометрично подібне проєкції на площину Коксетера.

Деякі гіперболічні сувої

Див. також

• Група Коксетера
• Трикутник Шварца
• Тетраедр Гурса
• Діаграма Динкіна
• Однорідний політоп
  • Символ Вітгофа
  • Однорідний багатогранник
  • Список однорідних багатогранників
  • Список плоских однорідних мозаїк
  • Однорідний 4-вимірний політоп
  • Опуклі однорідні стільники
  • Опуклі однорідні стільники в гіперболічному просторі
• Побудова Вітгофа і Символ Вітгофа

Література

• James E. Humphreys, Reflection Groups and Coxeter Groups, Cambridge studies in advanced mathematics, 29 (1990)
• Kaleidoscopes: Selected Writings of H.S.M. Coxeter / ed. by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss. — Wiley-Interscience Publication, 1995. — ISBN 978-0-471-01003-6. [2] [Архівовано 11 липня 2016 у Wayback Machine.], Googlebooks [3] [Архівовано 9 липня 2021 у Wayback Machine.]
• Coxeter. Chapter 3: Wythoff's Construction for Uniform Polytopes // The Beauty of Geometry: Twelve Essays. — Dover Publications, 1999. — ISBN 978-0-486-40919-1.
• H.S.M. Coxeter. Chapter 5: The Kaleidoscope, Section 11.3 Representation by graphs // Regular Polytopes. — Dover edition, 1973. — ISBN 0-486-61480-8.
• Г.С.М. Коксетер, У.О.Дж. Мозер. Порождающие элементы и определяющие соотношения дискретных групп = H.S.M. Coxeter, W. O. J. Moser, Generators and Relations for Discrete Groups. — Москва : Наука, 1980.
• Norman Johnson, Geometries and Transformations, Chapters 11,12,13, preprint 2011
• Norman Johnson, R. Kellerhals, J. G. Ratcliffe, S. T. Tschantz. Transformation Groups. — 1999. — Т. 4, вип. 4. — С. 329–353.
• Norman W. Johnson, Asia Ivic Weiss. Quadratic Integers and Coxeter Groups // Canad. J. Math. — 1999. — Т. 51, вип. 6. — С. 1307–1336.

Посилання

• Weisstein, Eric W. Coxeter–Dynkin diagram(англ.) на сайті Wolfram MathWorld.
• October 1978 discussion on the history of the Coxeter diagrams [Архівовано 10 червня 2015 у Wayback Machine.] by Coxeter and Dynkin in Toronto, Canada; Eugene Dynkin Collection of Mathematics Interviews, Бібліотека Корнелльського університету.