Зникома точка

Матеріал з Вікіпедії — вільної енциклопедії.
Перейти до навігації Перейти до пошуку
Цю сторінку запропоновано перейменувати на Точка сходу. Можливо, її поточна назва не відповідає нормам української мови або правилам іменування статей у Вікіпедії.
Пояснення причин і обговорення — на сторінці Вікіпедія:Перейменування статей.
Рухомий тротуар у франкфуртському аеропорту, тут видно зникому точку в кінці тунелю

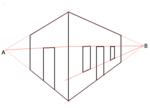
Знико́ма то́чка[1][2][3][4][неавторитетне джерело] (англ. vanishing point — букв. «точка зникнення») або то́чка схо́ду[5][6][7][8][9] (сходження)[9] — у графічній перспективі точка, де сходяться паралельні лінії. У випадку одно- чи двоточкової перспективи зникомі точки лежать на лінії обрію, у випадку триточкової перспективи третя точка лежить у зеніті чи надирі, залежно від того, знизу чи згори ведеться спостереження.

Якщо в реальному світі дві або більше прямих паралельні одна одній, але не паралельні щодо площини зображення, тоді вони мають одну й ту саму зникому точку. Перспективне зображення цих прямих не буде паралельним. Якщо прямі повністю розгорнуті на малюнку, зображені лінії перетинатимуться у зникомій точці.[10]

Означення[ред. | ред. код]

Формально зникома точка — це точка в площині зображення π, яка визначена прямою в просторі. Нехай задана точка розташування ока — O і пряма L не паралельна до π і нехай M буде прямою через O паралельною до L. Тоді зникома точка прямої L — це перетин M і π.[11]

Криволінійна і зворотна перспективи[ред. | ред. код]

Криволінійна перспектива — це зображення з 4 або 5 зникомими точками, у разі 5-точкової перспективи зникомі точки складають коло з 4 зникомими точками на головних курсах N, W, S, E й однією в центрі кола.

Зворотна перспектива — це зображення зі зникомими точками розташованими поза картиною з ілюзією, що вони «перед» картиною.

Аксонометричні проєкції[ред. | ред. код]

Аксонометричні проєкції — ізометрична, диметрична та триметрична розроблені для зображення об'єктів задля передачі технічної інформації. Вони використовують паралельні лінії, але не мають зникомих точок. Отже, їх не можна використовувати для реалістичного тривимірного малюнка[12].

  • Одноточкова перспектива
    Одноточкова перспектива
  • Двоточкова перспектива
    Двоточкова перспектива

Примітки[ред. | ред. код]

  1. ↑ Кузнєцов, П. С. (2023). Відновлення форми і розмірів об'єктів, зображених на розлінованих аркушах (PDF) (магістерська дисертація) (укр.). Київ: НТУУ «КПІ ім. Ігоря Сікорського». Архів оригіналу (PDF) за 13 листопада 2023. Процитовано 13 листопада 2023.
  2. ↑ Перспективне зображення з висоти пташиного польоту з однією зникомою точкою. House of Math (укр.). Архів оригіналу за 30 листопада 2022. Процитовано 13 листопада 2023.
  3. ↑ Перспективне зображення з жаб’ячої перспективи з однією зникомою точкою. House of Math (укр.). Архів оригіналу за 3 грудня 2022. Процитовано 13 листопада 2023.
  4. ↑ Червінська, Н. (2 березня 2023). Перспектива у фотографії: види й практичні поради для ефектних знімків. depositphotos (укр.). Архів оригіналу за 27 березня 2022. Процитовано 13 листопада 2023.
  5. ↑ Шпортько В. І. (2018). Робоча програма навчальної дисципліни «Перспектива» для студентів спеціальності 023 «Образотворче мистецтво, декоративне мистецтво, реставрація» (за видами) (PDF) (укр.). Київ: КМПУ ім. Б. Д. Грінченка. Архів оригіналу (PDF) за 13 листопада 2023. Процитовано 13 листопада 2023.
  6. ↑ ВИДИ ПЕРСПЕКТИВИ ТА МОЖЛИВОСТІ ЇХ ЗАСТОСУВАННЯ / Сидорова Н.В., Доценко Ю.В. // Науквий вісник Таврійського державного агротехнологічного університету : електронне фахове видання / Малкіна В.М.; коректор Мацулевич О.Є.. — Мелітополь : ТДАТУ, 2018. — Т. 1, вип. 8. — С. 69-78.
  7. ↑ Дизайн. Основи лінійної перспективи : навчально-методичний посібник / Лелик Я.Р. Тарасюк І.І. ; Східноєвропейський національний університет імені Лесі Українки. — Луцьк : ПП ВМА «Терен», 2019. — С. 11.
  8. ↑ Про доцільність застосування елементів проективної геометрії під час вивчення нарисної геометрії / Козяр, М. М.; Крівцов, В. В. // Наукові записки : [збірник наукових статей] / М-во освіти і науки України, Нац. пед. ун-т імені М. П. Драгоманова ; упор. Л. Л. Макаренко. — Київ : Вид-во НПУ імені М. П. Драгоманова, 2018. — Вип. СXХХІХ (139). — С. 105-114. — (Серія педагогічні науки).
  9. ↑ а б Бовкун С. А. Лінійна перспектива : навч. посіб.. — Запоріжжя : ЗНТУ, 2017. — ISBN 978-617-529-172-6.
  10. ↑ Lesson 3: Vanishing Points and Looking at Art (англ.)
  11. ↑ Kirsti Andersen (2007) Geometry of an Art, p. xxx, Springer, ISBN 0-387-25961-9
  12. ↑ 1, 2, & 3 Point Linear Perspective [Архівовано 28 вересня 2013 у Wayback Machine.] (англ.)
Отримано з https://uk.wikipedia.org/w/index.php?title=Зникома_точка&oldid=40914634