Колесо Арістотеля

«Ко́лесо Арісто́теля» — математичний парадокс, вперше описаний у книзі «Механіка», яка вважається працею Арістотеля (IV століття до н. е.)[1][2].
Формулювання[ред. | ред. код]
Розглянемо два з'єднаних колеса, одне всередині другого, із спільним центром (див. рисунок). Коли зовнішнє колесо рухається без ковзання по площині й описує повний оберт, його шлях дорівнює довжині кола, тобто його периметру. При цьому шлях внутрішнього колеса точно такий же, з чого можна зробити помилковий висновок, що величини їхніх периметрів (а, отже, і діаметри) рівні між собою.
Вирішення[ред. | ред. код]
Цей парадокс обговорювали багато видатних фізиків і математиків, у тому числі Галілей, Декарт, Ферма та ін.[3]
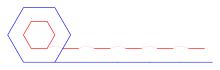
Варіація парадоксу з його вирішенням описана в «Двох нових науках» Галілея, де він розглядав пару концентричних шестикутників, а не кіл. Уявивши як вони котяться по поверхні, Галілей зауважив, що внутрішній шестикутник лишає лінію з невеликими розривами з кожним перекатом зовнішнього на нову грань; тоді як зовнішній лишає суцільну лінію. Якщо збільшувати кількість граней, наближуючи фігури до кола, ефект передбачувано зберігатиметься, лише стаючи менш помітним[4].

Першим правильний аналіз без спрощень дав Жан-Жак Дорту де Меран у 1715 році[5]. Як він пояснював, помилка полягає у допущенні, що колеса котяться без проковзування. Очевидно, що таке подвійне колесо не може котитись гладко обома коліями одночасно. Воно може котитись верхньою колією, але тоді більше колесо через ковзання постійно би відставало на нижній колії; або котилося б нижньою колією, але тоді менше колесо на верхній колії проковзувало б уперед. Таким чином точки на колесах рухаються по циклоїдах різної довжини, чиї початкові та кінцеві точки формують лінії однакової довжини[6].
Див. також[ред. | ред. код]
Примітки[ред. | ред. код]
- ↑ Гарднер, 1988, с. 13.
- ↑ Drabkin, Israel E. (1950). Aristotle's Wheel: Notes on the History of a Paradox. Osiris. 9: 162—198. Архів оригіналу за 27 червня 2020. Процитовано 26 листопада 2017.
- ↑ Гарднер, 1988, с. 13—15.
- ↑ Drake, Stillman (2000). Two new sciences, including centers of gravity and force of percussion. Toronto: Wall & Emerson. ISBN 0-921332-50-5. OCLC 44906056.
- ↑ Olivier Bruneau, Irène Passeron Des lions et des étoiles. Dortous de Mairan, un physicien distingué. Introduction, Revue d'histoire des sciences // Revue d'histoire des sciences, 2015/2, tome 68, P. (lire en ligne) [Архівовано 4 вересня 2017 у Wayback Machine.]
- ↑ Bunch, Bryan H. (1982). Mathematical Fallacies and Paradoxes. Van Nostrand Reinhold. с. 3–9. ISBN 0-442-24905-5.
Посилання[ред. | ред. код]
- Rota Aristotelica, The Archimedes Project, Digital Research Library
- Weisstein, Eric W. Aristotle's Wheel Paradox(англ.) на сайті Wolfram MathWorld.
| |||||||||||||||||||
