Ряд Фарея

Діаграма Фарея для послідовності $F_{9}$ з використанням дуг кіл. На SVG зображені наведіть курсор на криву, щоб виділити її та її члени.

Діаграма Фарея для $F_{9}$

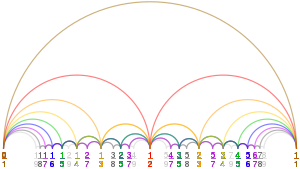
У математиці послідовність Фарея порядку $n$ — це послідовність нескоротних дробів, від 0 до 1, або без цього обмеження, знаменники яких менші або рівні $n$, а дроби розташовані в порядку зростання.

У рамках обмеженого означення кожна послідовність Фарея починається зі значення 0 (позначається як дріб ${\frac {0}{1}}$) і закінчується значенням 1 (позначається як дріб ${\frac {1}{1}}$), хоча деякі автори опускають ці члени.

Симетричний візерунок, утворений знаменниками послідовності Фарея $F_{9}$.

Послідовність Фарея іноді називають рядом Фарея, що не зовсім коректно, оскільки дроби не підсумовуються.

Симетричний візерунок, утворений знаменниками послідовності Фарея $F_{25}$.

Наприклад, ряд Фарея порядку 5:

$F_{5}=\left\{{\frac {0}{1}},\;{\frac {1}{5}},\;{\frac {1}{4}},\;{\frac {1}{3}},\;{\frac {2}{5}},\;{\frac {1}{2}},\;{\frac {3}{5}},\;{\frac {2}{3}},\;{\frac {3}{4}},\;{\frac {4}{5}},\;{\frac {1}{1}}\right\}.$

Приклади

Послідовність Фарея порядку від 1 до 8:

$F_{1}=\left\{{\frac {0}{1}},{\frac {1}{1}}\right\},$

$F_{2}=\left\{{\frac {0}{1}},{\frac {1}{2}},{\frac {1}{1}}\right\},$

$F_{3}=\left\{{\frac {0}{1}},{\frac {1}{3}},{\frac {1}{2}},{\frac {2}{3}},{\frac {1}{1}}\right\},$

$F_{4}=\left\{{\frac {0}{1}},{\frac {1}{4}},{\frac {1}{3}},{\frac {1}{2}},{\frac {2}{3}},{\frac {3}{4}},{\frac {1}{1}}\right\},$

$F_{5}=\left\{{\frac {0}{1}},{\frac {1}{5}},{\frac {1}{4}},{\frac {1}{3}},{\frac {2}{5}},{\frac {1}{2}},{\frac {3}{5}},{\frac {2}{3}},{\frac {3}{4}},{\frac {4}{5}},{\frac {1}{1}}\right\},$

$F_{6}=\left\{{\frac {0}{1}},{\frac {1}{6}},{\frac {1}{5}},{\frac {1}{4}},{\frac {1}{3}},{\frac {2}{5}},{\frac {1}{2}},{\frac {3}{5}},{\frac {2}{3}},{\frac {3}{4}},{\frac {4}{5}},{\frac {5}{6}},{\frac {1}{1}}\right\},$

$F_{7}=\left\{{\frac {0}{1}},{\frac {1}{7}},{\frac {1}{6}},{\frac {1}{5}},{\frac {1}{4}},{\frac {2}{7}},{\frac {1}{3}},{\frac {2}{5}},{\frac {3}{7}},{\frac {1}{2}},{\frac {4}{7}},{\frac {3}{5}},{\frac {2}{3}},{\frac {5}{7}},{\frac {3}{4}},{\frac {4}{5}},{\frac {5}{6}},{\frac {6}{7}},{\frac {1}{1}}\right\},$

$F_{8}=\left\{{\frac {0}{1}},{\frac {1}{8}},{\frac {1}{7}},{\frac {1}{6}},{\frac {1}{5}},{\frac {1}{4}},{\frac {2}{7}},{\frac {1}{3}},{\frac {3}{8}},{\frac {2}{5}},{\frac {3}{7}},{\frac {1}{2}},{\frac {4}{7}},{\frac {3}{5}},{\frac {5}{8}},{\frac {2}{3}},{\frac {5}{7}},{\frac {3}{4}},{\frac {4}{5}},{\frac {5}{6}},{\frac {6}{7}},{\frac {7}{8}},{\frac {1}{1}}\right\}.$

Відцентровані
$F_{1}=\left\{{\frac {0}{1}},{\frac {1}{1}}\right\}$
$F_{2}=\left\{{\frac {0}{1}},{\frac {1}{2}},{\frac {1}{1}}\right\}$
$F_{3}=\left\{{\frac {0}{1}},{\frac {1}{3}},{\frac {1}{2}},{\frac {2}{3}},{\frac {1}{1}}\right\}$
$F_{4}=\left\{{\frac {0}{1}},{\frac {1}{4}},{\frac {1}{3}},{\frac {1}{2}},{\frac {2}{3}},{\frac {3}{4}},{\frac {1}{1}}\right\}$
$F_{5}=\left\{{\frac {0}{1}},{\frac {1}{5}},{\frac {1}{4}},{\frac {1}{3}},{\frac {2}{5}},{\frac {1}{2}},{\frac {3}{5}},{\frac {2}{3}},{\frac {3}{4}},{\frac {4}{5}},{\frac {1}{1}}\right\}$
$F_{6}=\left\{{\frac {0}{1}},{\frac {1}{6}},{\frac {1}{5}},{\frac {1}{4}},{\frac {1}{3}},{\frac {2}{5}},{\frac {1}{2}},{\frac {3}{5}},{\frac {2}{3}},{\frac {3}{4}},{\frac {4}{5}},{\frac {5}{6}},{\frac {1}{1}}\right\}$
$F_{7}=\left\{{\frac {0}{1}},{\frac {1}{7}},{\frac {1}{6}},{\frac {1}{5}},{\frac {1}{4}},{\frac {2}{7}},{\frac {1}{3}},{\frac {2}{5}},{\frac {3}{7}},{\frac {1}{2}},{\frac {4}{7}},{\frac {3}{5}},{\frac {2}{3}},{\frac {5}{7}},{\frac {3}{4}},{\frac {4}{5}},{\frac {5}{6}},{\frac {6}{7}},{\frac {1}{1}}\right\}$
$F_{8}=\left\{{\frac {0}{1}},{\frac {1}{8}},{\frac {1}{7}},{\frac {1}{6}},{\frac {1}{5}},{\frac {1}{4}},{\frac {2}{7}},{\frac {1}{3}},{\frac {3}{8}},{\frac {2}{5}},{\frac {3}{7}},{\frac {1}{2}},{\frac {4}{7}},{\frac {3}{5}},{\frac {5}{8}},{\frac {2}{3}},{\frac {5}{7}},{\frac {3}{4}},{\frac {4}{5}},{\frac {5}{6}},{\frac {6}{7}},{\frac {7}{8}},{\frac {1}{1}}\right\}$

Відсортовані

F1 = {0/1, 1/1} F2 = {0/1, 1/2, 1/1} F3 = {0/1, 1/3, 1/2, 2/3, 1/1} F4 = {0/1, 1/4, 1/3, 1/2, 2/3, 3/4, 1/1} F5 = {0/1, 1/5, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5, 1/1} F6 = {0/1, 1/6, 1/5, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5, 5/6, 1/1} F7 = {0/1, 1/7, 1/6, 1/5, 1/4, 2/7, 1/3, 2/5, 3/7, 1/2, 4/7, 3/5, 2/3, 5/7, 3/4, 4/5, 5/6, 6/7, 1/1} F8 = {0/1, 1/8, 1/7, 1/6, 1/5, 1/4, 2/7, 1/3, 3/8, 2/5, 3/7, 1/2, 4/7, 3/5, 5/8, 2/3, 5/7, 3/4, 4/5, 5/6, 6/7, 7/8, 1/1}

Графік залежності чисельника від знаменника дробів послідовності Фарея має вигляд подібний до наведеного для послідовності $F_{6}$. Віддзеркаленя цієї фігури відносно діагоналі та координатних осей утворює сонячний спалах Фарея, як показано нижче.

Сонячний спалах Фарея порядку $n$ з'єднує видимі цілі точки решітки з початком координат у квадраті зі стороною $2n$ і центром у початку координат. Відповідно до теореми Піка, площа сонячного спалаху Фарея дорівнює $4(|F_{n}|-1)$, де $|F_{n}|$ ― кількість дробів у послідовності $F_{n}$.

Ітерації 1–10

Історія

Історія «рядів Фарея» дуже цікава — Харді і Райт (1979)

… і знову людина, чиє ім'я було дано математичному поняттю, не була його першовідкривачем, якщо вірити записам. — Бейлер (1964)

Послідовність Фарея названа на честь британського геолога Джона Фарея старшого, який 1816 року опублікував замітку про ці послідовності у Філософському журналі. Він припустив, але без жодних доведень, що кожен новий дріб у послідовності є медіантою його сусідів. Замітку Фарея прочитав Коші, який довів цю гіпотезу в своїй роботі Exerces de mathématique, і приписав цей результат Фарею. Насправді, інший математик, Чарльз Гарос, ще 1802 року опублікував аналогічні результати, які не були відомі ні Фарею, ні Коші. Тому зв'язок Фарея з цією послідовністю просто історична випадковість. Це приклад вияву закону Стіглера про епонімію.

Властивості

Довжина послідовності та індекс дробу

Послідовність Фарея порядку $n$ містить усі члени послідовностей нижчих порядків. Зокрема, послідовність $F_{n}$ містить усі члени послідовності $F_{n-1}$ та додаткові дроби для кожного числа, яке менше $n$, та є взаємно простим з $n$. Таким чином, послідовність $F_{6}$ складається з послідовності $F_{5}$ та дробів ${\frac {1}{6}}$ і ${\frac {5}{6}}$.

Середнім дробом для послідовності Фарея $F_{n}$ завжди є ${\frac {1}{2}}$, за умови що $n>1$. Тому можемо пов'язати довжини послідовностей $F_{n}$ і $F_{n-1}$ за допомогою функції Ейлера $\varphi (n)$:

$|F_{n}|=|F_{n-1}|+\varphi (n).$

Використовуючи той факт, що $|F_{1}|=2$, можна вивести співвідношення для довжини послідовності $F_{n}$ :

$|F_{n}|=1+\sum _{m=1}^{n}\varphi (m)=1+\Phi (n),$

де $\Phi (n)$ ― сумарна тотієнт функція.

Також довжину послідовності $F_{n}$ можна знайти за формулою:

$|F_{n}|={\frac {1}{2}}\left(3+\sum _{d=1}^{n}\mu (d)\left\lfloor {\frac {n}{d}}\right\rfloor ^{2}\right),$

або за формулою інверсії Мебіуса:

$|F_{n}|={\frac {1}{2}}(n+3)n-\sum _{d=2}^{n}|F_{\lfloor {\frac {n}{d}}\rfloor }|,$

де $\mu (d)$ ― теоретико-числова функція Мебіуса, $\lfloor {\tfrac {n}{d}}\rfloor$ ― функція підлоги.

Асимптотична поведінка послідовності $|F_{1}|$ визначається за формулою:

$|F_{n}|\sim {\frac {3n^{2}}{\pi ^{2}}}.$

Індекс $I_{n}(a_{k,n})=k$ для дробу $a_{k,n}$ у послідовності Фарея $F_{n}=\{a_{k,n}\colon k=0,1,\ldots ,m_{n}\}$ це позиція, яку дріб $a_{k,n}$ займає в послідовності. Поняття індекса має особливе значення, оскільки використовується в альтернативному формулюванні гіпотези Рімана. Деякі корисні властивості:

$I_{n}(0/1)=0,$

$I_{n}(1/n)=1,$

$I_{n}(1/2)=(|F_{n}|-1)/2,$

$I_{n}(1/1)=|F_{n}|-1,$

$I_{n}(h/k)=|F_{n}|-1-I_{n}((k-h)/k).$

Індекс дробу ${\frac {1}{k}}$, де ${\frac {n}{i+1}}<k\leq {\frac {n}{i}}$ і $n$ є найменшим спільним кратним перших $i$ чисел, тобто $n={\rm {lcm}}([2,i])$, обчислюється за формулою:

$I_{n}\left({\frac {1}{k}}\right)=1+n\sum _{j=1}^{i}{\frac {\varphi (j)}{j}}-k\Phi (i).$

Сусіди Фарея

Дроби, які є сусідніми в будь-якій послідовності Фарея, називають парами Фарея, вони мають такі властивості: Якщо ${\frac {a}{b}}$ і ${\frac {c}{d}}$ ― пара Фарея, при чому ${\frac {a}{b}}<{\frac {c}{d}}$, то їх різниця ${\frac {a}{b}}-{\frac {c}{d}}$ дорівнює ${\frac {1}{bd}}$. Це пов'язано з тим, що кожна послідовна пара раціональних чисел Фарея має еквівалентну площу 1.

Якщо $r_{1}={\frac {p}{q}}$ і $r_{2}={\frac {p'}{q'}}$ розглядати як вектори $(p,q)$ у площині $xy$, то площа $A\left({\frac {p}{q}},{\frac {p'}{q'}}\right)$ обчислюється як $qp'-q'p$. Оскільки будь-який дріб між двома попередніми послідовними дробами послідовності Фарея обчислюється як медіанта $(\oplus )$, то

$A(r_{1},r_{1}\oplus r_{2})=A(r_{1},r_{1}+A(r_{1},r_{2}+A(r_{1},r_{2}))=1$

(оскільки $r_{1}=1/0$ і $r_{2}=0/1$, то його площа повинна дорівнювати одиниці).

Оскільки ${\frac {c}{d}}-{\frac {a}{b}}={\frac {bc-ad}{bd}}$, то це еквівалентно умові $bc-ad=1$. Таким чином, ${\frac {1}{3}}$ і ${\frac {2}{5}}$ ― сусіди в послідовності $F_{5}$, і їх різниця дорівнює ${\frac {1}{15}}$.

Обернене також істинне. Якщо

$bc-ad=1$

для натуральних чисел $a$, $b$, $c$ і $d$ та $a<b$ і $c<d$, то дроби ${\frac {a}{b}}$ і ${\frac {c}{d}}$ ― пара Фарея порядку $\max(b,d)$.

Якщо ${\frac {p}{q}}$ має сусідів ${\frac {a}{b}}$ і ${\frac {c}{d}}$ у деякій послідовності Фарея, причому

${\frac {a}{b}}<{\frac {p}{q}}<{\frac {c}{d}}$,

то ${\frac {p}{q}}$ є медіантою дробів ${\frac {a}{b}}$ і ${\frac {c}{d}}$. Іншими словами:

${\frac {p}{q}}={\frac {a+c}{b+d}}$.

Це легко випливає з попередньої властивості, оскільки якщо $bp-aq=qc-pd=1,$ то $bp+pd=qc+aq$, $p(b+d)=q(a+c)$, ${\frac {p}{q}}={\frac {a+c}{b+d}}$.

З цього випливає, що якщо ${\frac {a}{b}}$ і ${\frac {c}{d}}$ є парою Фарея, то першим членом, який з'являється між ними при збільшенні порядку послідовності, буде ${\frac {a+c}{b+d}}$, і він же буде першим членом послідовності Фарея порядку $b+d$.

Наприклад, першим дробом, що з'являється між ${\frac {1}{3}}$ і ${\frac {2}{5}}$, є ${\frac {3}{8}}$ у послідовності $F_{8}$.

Загальна кількість пар Фарея в послідовності $F_{n}$ становить $2F_{n}-3$.

Дерево Штерна — Броко ― це структура даних, яка показує побудову послідовності з 0 (= ${\frac {0}{1}}$) і 1 (= ${\frac {1}{1}}$) за допомогою послідовних медіант.

Сусіди Фарея та ланцюгові дроби

Дроби, що з'являються як сусіди в послідовності Фарея тісно пов'язані з розкладами ланцюгових дробів. Кожен дріб має два розклади на неперевні дроби ― один кінцевий член дорівнює 1, інший ― більший за 1. Якщо дріб ${\frac {p}{q}}$, який уперше з'являється в послідовності Фарея $F_{q}$, допускає розклади у вигляді ланцюгових дробів

$[0,a_{1},a_{2},\ldots ,a_{n-1},a_{n},1],$

$[0,a_{1},a_{2},\ldots ,a_{n-1},a_{n}+1],$

то один сусідній дріб дробу ${\frac {p}{q}}$ (який є його сусідом із більшим знаменником) у послідовності $F_{q}$ має розклад у ланцюговий дріб вигляду

$[0;a_{1},a_{2},\ldots ,a_{n}],$

а його інший сусід має розклад у ланцюговий дріб вигляду

$[0;a_{1},a_{2},\ldots ,a_{n-1}].$

Наприклад ${\frac {3}{8}}$ має два розклади у вигляді ланцюгових дробів: $[0;2,1,1,1]$ та $[0;2,1,2]$, а його сусідами в послідовності $F_{8}$ є ${\frac {2}{5}}$, який можна розкласти як $[0;2,1,1]$, та ${\frac {1}{3}}$, який можна розкласти як $[0;2,1]$.

Дроби Фарея та найменше спільне кратне

Найменше спільне кратне можна представити у вигляді добутку дробів послідовності Фарея

${\text{lcm}}[1,2,\dots ,N]=e^{\psi (N)}={\frac {1}{2}}\left(\prod _{r\in F_{N},0<r\leq 1/2}2\sin(\pi r)\right)^{2},$

де $\psi (N)$ ― друга функція Чебишова.

Дроби Фарея та найбільший спільний дільник

Оскільки функція Ейлера безпосередньо пов'язана з найбільшим спільним дільником, так само як і кількість елементів у $F_{n}$, то $|F_{n}|$ можна обчислити за формулою:

$|F_{n}|=1+\sum _{m=1}^{n}\varphi (m)=1+\sum \limits _{m=1}^{n}\sum \limits _{k=1}^{m}\gcd(k,m)\cos {2\pi {\frac {k}{m}}}.$

Для будь-яких трьох дробів послідовності Фарея ${\frac {a}{b}}$, ${\frac {c}{d}}$ і ${\frac {e}{f}}$ виконується рівність для найбільших спільних дільників абсолютних значень визначників матриць розмірності 2x2:,

$\gcd \left({\begin{Vmatrix}a&c\\b&d\end{Vmatrix}},{\begin{Vmatrix}a&e\\b&f\end{Vmatrix}}\right)=\gcd \left({\begin{Vmatrix}a&c\\b&d\end{Vmatrix}},{\begin{Vmatrix}c&e\\d&f\end{Vmatrix}}\right)=\gcd \left({\begin{Vmatrix}a&e\\b&f\end{Vmatrix}},{\begin{Vmatrix}c&e\\d&f\end{Vmatrix}}\right).$

Застосування

Послідовності Фарея дуже корисні для пошуку раціональних наближень ірраціональних чисел. Наприклад, побудова Еліахау нижньої межі довжини нетривіальних циклів у $3x+1$ процесі використовує послідовності Фарея для обчислення розкладу в ланцюговий дріб числа $\log _{2}(3)$.

У фізичних системах із резонансними явищами послідовності Фарея забезпечують дуже простий і ефективний метод обчислення резонансних позицій для розмірностей 1 та 2.

Послідовності Фарея посідають важливе місце в дослідженнях планування шляху під будь-яким кутом на клітинках квадратів сітки, наприклад, для характеристики їх обчислювальної складності або оптимальності. З'єднання можна розглядати з точки зору $r$-обмежених шляхів, а саме шляхів, які складаються з відрізків, кожен з яких перетинає максимум $r$ рядків і не більше $r$ стовпців клітинок. Нехай $Q$ ― множина взаємнопростих векторів $(q,p)$ таких, що $1\leq q\leq r$, $0\leq p\leq q$. Нехай $Q*$ ― результат відбиття множини $Q$ відносно прямої $y=x$. Нехай $S=\{(\pm x,\pm y)\colon (x,y)\in Q\cup Q*\}.$ Тоді будь-який $r$-обмежений шлях можна описати як послідовність векторів з $S$. Існує бієкція між множиною $Q$ і послідовністю Фарея порядку $r$, заданою відображенням вектора $(q,p)$ на дріб ${\frac {p}{q}}$.

Кола Форда

Порівняння кіл Форда і діаграми Фарея з круговими дугами для $n$ від 1 до 9. Кожна дуга перетинає відповідні кола під прямим кутом. На svg-рисунку наведіть вказівник на коло чи криву, щоб виділити їх або їх елементи.

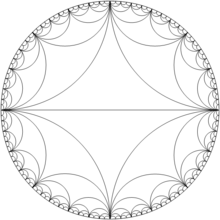
Існує зв'язок між послідовністю Фарея і колами Форда.

Для кожного дробу ${\frac {p}{q}}$ (в його найменших термінах) існує коло Форда $C\left[{\frac {p}{q}}\right]$ з радіусом ${\frac {1}{2q^{2}}}$ і центром у точці $\left({\frac {p}{q}},{\frac {1}{2q^{2}}}\right)$. Два кола Форда для різних дробів або не перетинаються, або дотикаються ― кола Форда ніколи не перетинаються. Якщо $0<{\frac {p}{q}}<1$, то кола Форда, які дотичні до кола $C\left[{\frac {p}{q}}\right]$ є колами Форда для дробів, які є сусідами дробу ${\frac {p}{q}}$ в деякій послідовності Фарея. Таким чином, коло $C\left[{\frac {2}{5}}\right]$ є дотичним до кіл $C\left[{\frac {1}{2}}\right]$, $C\left[{\frac {1}{3}}\right]$, $C\left[{\frac {3}{7}}\right]$, $C\left[{\frac {3}{8}}\right]$ тощо.

Сітка Аполлонія $(0,0,1,1)$ і резонансна діаграма Фарея.

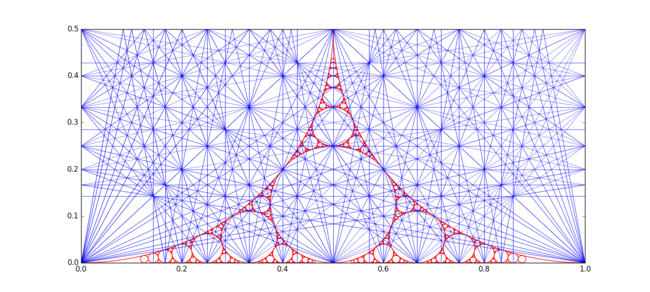
Кола Форда з'являються також у сітці Аполлонія $(0,0,1,1)$. Рисунок нижче ілюструє це разом з резонансними лініями послідовності Фарея.

Гіпотеза Рімана

Послідовності Фарея використовуються в двох формулюваннях гіпотези Рімана. Нехай $F_{n}$ є $\{{a_{k,n}\colon \ k=0,1,\ldots ,m_{n}}\}.$ Визначити $d_{k,n}=a_{k,n}-{\frac {k}{m_{n}}},$ іншими словами $d_{k,n}$ ― різниця між $k$-м членом $n$-ї послідовності Фарея і $k$-м членом множини з тією ж кількістю точок, розміщених на однаковій відстані одна від одної на одиничному інтервалі. У 1924 році Жером Франель довів, що твердження

$\sum _{k=1}^{m_{n}}d_{k,n}^{2}=O(n^{r}),\quad \forall r>1/2,$

еквівалентне гіпотезі Рімана, а потім Едмунд Ландау зауважив (відразу після статті Франеля), що твердження

$\sum _{k=1}^{m_{n}}|d_{k,n}|=O(n^{r}),\quad \forall r>-1,$

також еквівалентне гіпотезі Рімана.

Інші суми з дробами Фарея

Сума всіх дробів послідовності Фарея порядку $n$ дорівнює половині кількості елементів цієї послідовності:

$\sum _{r\in F_{n}}r={\frac {1}{2}}|F_{n}|.$

Сума знаменників у послідовності Фарея в два рази перевищує суму чисельників і може бути представлена функцією Ейлера:

$\sum {{\frac {a}{b}}\in F_{n}}b=2\sum {{\frac {a}{b}}\in F_{n}}a=1+\sum _{i=1}^{n}i\varphi (i).$

Цю гіпотезу висунув Гарольд Л. Аарон у 1962 році, а довів Джин А. Блейк у 1966 році. Доведення в один рядок гіпотези Гарольда Л. Аарона таке. Сума чисельників дорівнює:

$1+\sum _{2\leq b\leq n}\sum _{(a,b)=1}a=1+\sum _{2\leq b\leq n}b{\frac {\varphi (b)}{2}}.$

Сума знаменників дорівнює:

$2+\sum _{2\leq b\leq n}\sum _{(a,b)=1}b=2+\sum _{2\leq b\leq n}b\varphi (b).$

Відношення першої суми до другої дорівнює ${\frac {1}{2}}$.

Нехай $b_{j}$ — впорядковані знаменники послідовності $F_{n}$, тоді

$\sum _{j=0}^{|F_{n}|-1}{\frac {b_{j}}{b_{j}+1}}={\frac {3|F_{n}|-4}{2}},$

і

$\sum _{j=0}^{|F_{n}|-1}{\frac {1}{b_{j=1}+b_{j}}}=1.$

Нехай ${\frac {a_{j}}{b_{j}}}$ — $j$-й дріб послідовності Фарея $F_{n}$, тоді

$\sum _{j=1}^{|F_{n}|-1}(a_{j-1}b_{j+1}-a_{j+1}b_{j-1})=\sum _{j=1}^{|F_{n}|-1}{\begin{Vmatrix}a_{j-1}&a_{j+1}\\b_{j-1}&b_{j+1}\end{Vmatrix}}=3(|F_{n}|-1)-2n-1,$

як показано в роботі Галла і Шіу. Також, згідно з цією роботою, член всередині суми можна представити багатьма різними способами:

$a_{j-1}b_{j+1}-a_{j+1}b_{j-1}={\frac {b_{j-1}+b_{j+1}}{b_{j}}}={\frac {a_{j-1}+a_{j+1}}{a_{j}}}=\left\lfloor {\frac {n+b_{j+1}}{b_{j}}}\right\rfloor ,$

отримуючи таким чином багато різних сум за елементами послідовності Фарея з однаковим результатом. Використовуючи симетрію відносно ${\frac {1}{2}}$, суму можна обмежити половиною послідовності:

$\sum _{j=1}^{|F_{n}|/2}a_{j-1}b_{j+1}-a_{j+1}b_{j-1}=3(|F_{n}|-1)/2-n-\lceil n/2\rceil .$

Функцію Мертенса можна подати як суму дробів послідовності Фарея в такий спосіб:

$M(n)=-1+\sum _{a\in {\mathcal {F}}_{n}}{\rm {e}}^{2\pi {\rm {i}}a},$

де ${\mathcal {F}}_{n}$ ― послідовність Фарея порядку $n$. Ця формула використовується в доведенні теореми Франеля ― Ландау.

Наступний член

Існує надзвичайно простий алгоритм для обчислення дробів у послідовності Фарея $F_{n}$ в традиційному порядку (зростання) або нетрадиційному порядку (спадання). Алгоритм обчислює кожен наступний елемент, враховуючи попередні два і застосовуючи до них властивість медіанти. Якщо ${\frac {a}{b}}$ і ${\frac {c}{d}}$ — два відомі елементи, і ${\frac {p}{q}}$ ― невідомий наступний елемент, то ${\frac {c}{d}}={\frac {a+p}{b+q}}$. Оскільки ${\frac {c}{d}}$ нескоротний дріб, то існує ціле число $k$ таке, що $kc=a+p$ і $kd=b+q$, а тому $p=kc-a$ і $q=kd-b$. Якщо розглядати $p$ і $q$ як функції від $k$, то

${\frac {p(k)}{q(k)}}-{\frac {c}{d}}={\frac {cb-da}{d(kd-b)}},$

тому чим більше беремо $k$, тим ближче ${\frac {p}{q}}$ розташовується до ${\frac {c}{d}}$.

Щоб знайти наступний дріб у послідовності Фарея, $k$ має бути якомога більшим, враховуючи що $kd-b\leq n$ (оскільки розглядаємо лише числа зі знаменниками не більше $n$), то $k$ ― найбільше ціле число, $k\leq {\frac {n+b}{d}}$. Підставляючи це значення $k$ у співвідношення для $p$ і $q$ отримуємо:

$p=\left\lfloor {\frac {n+b}{d}}c-a\right\rfloor ,$

$q=\left\lfloor {\frac {n+b}{d}}d-b\right\rfloor .$

Цей алгоритм можна реалізувати мовою Python так:

def farey_sequence(n: int, descending: bool = False) -> None:
    """Print the n'th Farey sequence. Allow for either ascending or descending."""
    (a, b, c, d) = (0, 1, 1, n)
    if descending:
        (a, c) = (1, n - 1)
    print("{0}/{1}".format(a, b))
    while (c <= n and not descending) or (a > 0 and descending):
        k = (n + b) // d
        (a, b, c, d) = (c, d, k * c - a, k * d - b)
        print("{0}/{1}".format(a, b))

Для прямого знаходження розв'язків діофантових рівнянь у раціональних числах часто можна використовувати ряди Фарея (для знаходження лише зведених форм). Рядки з позначкою $(*)$ також можна змінити, щоб включити будь-які два суміжних члени для отримання членів лише більших (або менших) ніж заданий член.

Див. також

• Дерево Штерна — Броко
• Шаблон ABACABA
• Функція Ейлера

Джерела

1. Математическая энциклопедия. В пяти томах. Том 5./ Под ред. И. М. Виноградова. М.: Советская энциклопедия, 1984, с. 598

Література

• Hatcher, Allen. Topology of Numbers. Mathematics. Ithaca, NY: Cornell U.
• Graham, Ronald L.; Knuth, Donald E.; Patashnik, Oren (1989). Concrete Mathematics: A foundation for computer science (вид. 2nd). Boston, MA: Addison-Wesley. с. 115—123, 133—139, 150, 462—463, 523—524. ISBN 0-201-55802-5. — in particular, see § 4.5 (pp. 115–123), Bonus Problem 4.61 (pp. 150, 523—524), § 4.9 (pp. 133–139), § 9.3, Problem 9.3.6 (pp. 462–463).
• Vepstas, Linas. The Minkowski Question Mark, GL(2,Z), and the Modular Group (PDF). — reviews the isomorphisms of the Stern-Brocot Tree.
• Vepstas, Linas. Symmetries of Period-Doubling Maps (PDF). — reviews connections between Farey Fractions and Fractals.
• Cobeli, Cristian; Zaharescu, Alexandru (2003). The Haros-Farey sequence at two hundred years. A survey. Acta Univ. Apulensis Math. Inform. (5): 1—38. pp. 1–20 (PDF). Acta Univ. Apulensis. pp. 21–38 (PDF). Acta Univ. Apulensis.
• Matveev, Andrey O. (2017). Farey Sequences: Duality and Maps Between Subsequences. Berlin, DE: De Gruyter. ISBN 978-3-11-054662-0.

Посилання

• Bogomolny, Alexander. Farey series. Cut-the-Knot.
• Bogomolny, Alexander. Stern-Brocot Tree. Cut-the-Knot.
• Pennestri, Ettore. A Brocot table of base 120.
• «Farey series», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Weisstein, Eric W. Stern-Brocot Tree(англ.) на сайті Wolfram MathWorld.
• Число дробів у ряді Фарея порядку n — послідовність A005728 з Онлайн енциклопедії послідовностей цілих чисел, OEIS
• Чисельники ряду Фарея порядку n — послідовність A006842 з Онлайн енциклопедії послідовностей цілих чисел, OEIS
• Знаменники ряду Фарея порядку n — послідовність A006843 з Онлайн енциклопедії послідовностей цілих чисел, OEIS
• Archived at Ghostarchive and the Wayback Machine: Bonahon, Francis. Funny Fractions and Ford Circles (video). Brady Haran. Процитовано 9 червня 2015 — через YouTube.

Посилання

• Weisstein, Eric W. Послідовність Фарея(англ.) на сайті Wolfram MathWorld.