Граф Турана

Граф Турана
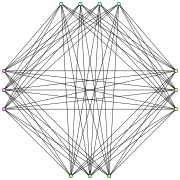Граф Турана T(13,4)
Названо на честь	Пал Туран
Вершин	n
Ребер	~${\frac {(r-1)n^{2}}{2r}}$
Радіус	$\left\{{\begin{array}{ll}\infty &r=1\\2&r\leq n/2\\1&{\text{otherwise}}\end{array}}\right.$
Діаметр	$\left\{{\begin{array}{ll}\infty &r=1\\1&r=n\\2&{\text{otherwise}}\end{array}}\right.$
Обхват	$\left\{{\begin{array}{ll}\infty &r=1\vee (n\leq 3\wedge r\leq 2)\\4&r=2\\3&{\text{otherwise}}\end{array}}\right.$
Хроматичне число	r
Позначення	T(n,r)

Граф Турана T(n,r) — це граф, утворений розкладанням n вершин на r підмножин, з якомога ближчим розміром, і вершини в цьому графі з'єднані ребром, якщо вони належать різним підмножинам. Граф буде мати $(n\,{\bmod {\,}}r)$ підмножин розміром $\lceil n/r\rceil$ і $r-(n\,{\bmod {\,}}r)$ підмножин розміром $\lfloor n/r\rfloor$. Таким чином, це повний r-частковий граф

$K_{\lceil n/r\rceil ,\lceil n/r\rceil ,\ldots ,\lfloor n/r\rfloor ,\lfloor n/r\rfloor }.$

Кожна вершина має степінь або $n-\lceil n/r\rceil$, або $n-\lfloor n/r\rfloor$. Кількість ребер дорівнює

${\frac {1}{2}}(n^{2}-(n\,{\bmod {\,}}r)\lceil n/r\rceil ^{2}-(r-(n\,{\bmod {\,}}r))\lfloor n/r\rfloor ^{2})\leq \left(1-{\frac {1}{r}}\right){\frac {n^{2}}{2}}.$

Граф є регулярним, якщо n ділиться на r.

Теорема Турана

Графи Турана названо на честь Пала Турана, який використав їх для доведення теореми Турана, важливого результату в екстремальній теорії графів.

За принципом Діріхле, будь-яка множина з r + 1 вершин у графі Турана включає дві вершини з однієї й тієї ж частки графа. Таким чином, граф Турана не містить кліки розміру r + 1. Згідно з теоремою Турана, граф Турана має максимально можливе число ребер серед усіх графів без клік розміру r + 1, що мають n вершин. Киваш і Судаков (Keevash, Sudakov, 2003) показали, що граф Турана є єдиним графом без клік розміру r + 1, що має порядок n, у якому будь-яка підмножина з αn вершин має щонайменше ${\frac {r\,{-}\,1}{2r}}(2\alpha -1)n^{2}$ ребер, якщо α досить близьке до 1. Теорема Ердеша — Стоуна розширює теорему Турана, обмежуючи число ребер у графі, який не має підграфом фіксованого графу Турана. Внаслідок цієї теореми в теорії екстремальних графів для будь-якого забороненого підграфу можна довести схожі межі, залежні від хроматичного числа підграфу.

Особливі випадки

Октаедр, вершини і ребра якого утворюють граф Турана T(6,3).

Деякі величини параметра r графів Турана призводять до чудових графів, які вивчаються окремо.

Граф Турана T(2n,n) можна отримати видаленням досконалого парування з повного графа K_2n. Як показав Робертс (Roberts, 1969), рамковість цього графу дорівнює рівно n. Цей граф іноді називають графом Робертса. Цей граф є також 1-скелетом n-вимірного кографа. Наприклад, граф T(6,3) = K_2,2,2 — це граф правильного октаедра. Якщо n пар приходять на вечірку і кожна людина тисне руку всім, окрім свого партнера, то цей граф описує множину рукостискань. З цієї причини його також називають графом коктейль-вечірки.

Граф Турана T(n,2) — це повний двочастковий граф, і, якщо n парне, це граф Мура. Якщо r — це дільник n, граф Турана є симетричним і сильно регулярним, хоча деякі автори вважають, що графи Турана є тривіальним випадком сильної регулярності і тому виключають їх з визначення строго регулярних графів.

Граф Турана $T(n,\lceil n/3\rceil )$ має 3^a2^b найбільших клік, де 3a + 2b = n та b ≤ 2. Кожна найбільша кліка утворюється вибором однієї вершини з кожної частки. Це число найбільших клік є найбільшим можливим серед усіх графів з n вершинами, незалежно від числа ребер у графі (Мун і Мозер, 1965). Ці графи іноді називають графами Муна-Мозера.

Інші властивості

Будь-який граф Турана є кографом. Таким чином, його можна утворити з окремих вершин послідовністю операцій диз'юнктного об'єднання і доповнення. Зокрема, таку послідовність можна почати утворенням усіх незалежних множин графу Турана як диз'юнктного об'єднання ізольованих вершин. Тоді весь граф є доповненням диз'юнктного об'єднання доповнень цих незалежних множин.

Чао і Новацький (Chao, Novacky, 1982) показали, що графи Турана хроматично єдині — ніякі інші графи не мають таких самих хроматичних многочленів. Нікіфоров (Nikiforov, 2005) використовував графи Турана для знаходження нижньої межі суми k-х власних значень графу і його доповнення.

Фолс, Повел і Сноїнк (Falls, Powell, Snoeyink) розробили ефективний алгоритм для пошуку кластерів ортологічних груп генів у геномі поданням даних як графу і пошуком великих підграфів Турана.

Графи Турана мають також низку цікавих властивостей, пов'язаних з геометричною теорією графів. Пор і Вуд (Pór, Wood, 2005) дають нижню межу Ω((rn)^3/4) будь-якого тривимірного вкладення графу Турана. Вітсенгаузен (Witsenhausen, 1974) висловив гіпотезу, що найбільша сума квадратів відстаней між n точками всередині кулі R^d одиничного діаметра досягається на конфігурації, утвореній вкладенням графу Турана у вершини правильного симплекса.

Граф G з n вершинами є підграфом графу Турана T(n,r) тоді й лише тоді, коли G допускає рівномірне розфарбування в r кольорів. Розкладання графу Турана на незалежні множини відповідає розкладанню G на класи кольорів. Зокрема, граф Турана є єдиним максимальним графом з n вершинами з рівномірним розфарбуванням у r кольорів.

Література

• C. Y. Chao, G. A. Novacky. On maximally saturated graphs // Discrete Mathematics. — 1982. — Т. 41, вип. 2 (25 квітня). — С. 139–143. — DOI:10.1016/0012-365X(82)90200-X.
• Craig Falls, Bradford Powell, Jack Snoeyink. Computing high-stringency COGs using Turán type graphs.
• Peter Keevash, Benny Sudakov. Local density in graphs with forbidden subgraphs // Combinatorics, Probability and Computing. — 2003. — Т. 12, вип. 2 (25 квітня). — С. 139–153. — DOI:10.1017/S0963548302005539.
• J. W. Moon, L. Moser. On cliques in graphs // Israel Journal of Mathematics. — 1965. — Т. 3 (25 квітня). — С. 23–28. — DOI:10.1007/BF02760024.
• Vladimir Nikiforov. Eigenvalue problems of Nordhaus-Gaddum type. — 2005. — 25 квітня. — arXiv:math.CO/0506260.
• Attila Pór, David R Wood. Proc. Int. Symp. Graph Drawing (GD 2004). — Lecture Notes in Computer Science no. 3383, Springer-Verlag, 2005. — С. 395–402. — DOI:10.1007/b105810.
• F. S. Roberts. Recent Progress in Combinatorics. — Academic Press, 1969. — С. 301–310.
• P. Turán. On an extremal problem in graph theory // Matematiko Fizicki Lapok. — 1941. — Т. 48 (25 квітня). — С. 436–452.
• H. S. Witsenhausen. On the maximum of the sum of squared distances under a diameter constraint // American Mathematical Monthly. — The American Mathematical Monthly, Vol. 81, No. 10, 1974. — Т. 81, вип. 10 (25 квітня). — С. 1100–1101. — DOI:10.2307/2319046.

Посилання

• Weisstein, Eric W. Cocktail Party Graph(англ.) на сайті Wolfram MathWorld.
• Weisstein, Eric W. Граф октаедра(англ.) на сайті Wolfram MathWorld.
• Weisstein, Eric W. Граф Турана(англ.) на сайті Wolfram MathWorld.