Структурний тензор

Виявляння ознак
Виявляння контурів
Кенні Деріша Диференціальне Собеля Прюітт Робертса
Виявляння кутів
Гарріса Сі та Томазі Кривина ізоліній міри вираженості гессіанових ознак SUSAN FAST
Виявляння плям
Лапласіан гауссіана (ЛГ, LoG) Різниця гауссіанів (РГ, DoG) Визначник гессіана (ВГ, DoH) МСЕО (MSER) PCBR
Виявляння хребтів
Перетворення Гафа
Перетворення Гафа Узагальнене перетворення Гафа
Структурний тензор
Структурний тензор Узагальнений структурний тензор
Афінноінваріантне виявляння ознак
Афінне пристосовування форми Афінне Гарріса Афінне гесіанне
Опис ознак
SIFT SURF GLOH HOG
Простір масштабів
Масштабопросторові аксіоми Деталі втілення Піраміди

У математиці структу́рний те́нзор (англ. structure tensor), відомий також як ма́триця дру́гого моме́нту (англ. second-moment matrix), — це матриця, яку виводять з градієнта функції. Він описує розподіл градієнта в заданому околі навколо точки, та робить цю інформацію інваріантною щодо координат спостереження. Структурний тензор часто використовують в обробці зображень та комп'ютерному баченні.

Двовимірний структурний тензор

Неперервний варіант

Для функції $I$ двох змінних p = (x, y) структурний тензор — це матриця 2×2

$S_{w}(p)={\begin{bmatrix}\int w(r)(I_{x}(p-r))^{2}\,dr&\int w(r)I_{x}(p-r)I_{y}(p-r)\,dr\\[10pt]\int w(r)I_{x}(p-r)I_{y}(p-r)\,dr&\int w(r)(I_{y}(p-r))^{2}\,dr\end{bmatrix}}$

де $I_{x}$ та $I_{y}$ — частинні похідні $I$ відносно x та y; інтеграли пробігають площину $\mathbb {R} ^{2}$; а w — деяка фіксована «віконна функція» (така як гауссове розмиття), розподіл двох змінних. Зверніть увагу, що матриця $S_{w}$ сама є функцією p = (x, y).

Наведену вище формулу можливо також записати як $S_{w}(p)=\int w(r)S_{0}(p-r)\,dr$, де $S_{0}$ — матрицезначна функція, визначена як

$S_{0}(p)={\begin{bmatrix}(I_{x}(p))^{2}&I_{x}(p)I_{y}(p)\\[10pt]I_{x}(p)I_{y}(p)&(I_{y}(p))^{2}\end{bmatrix}}$

Якщо градієнт $\nabla I=(I_{x},I_{y})^{\text{T}}$ функції $I$ розглядати як матрицю 2×1 (одностовпчикову), де $(.)^{\text{T}}$ позначує операцію транспонування, яке перетворює рядковий вектор на стовпчиковий, то матрицю $S_{0}$ можливо записати як матричний добуток $(\nabla I)(\nabla I)^{\text{T}}$ або тензорний чи зовнішній добуток $\nabla I\otimes \nabla I$. Проте зауважте, що структурний тензор $S_{w}(p)$ неможливо розкладати таким чином у загальному випадку, за винятком, коли $w$ — дельта-функція Дірака.

Дискретний варіант

В обробці зображень та інших подібних застосуваннях функцію $I$ зазвичай задають дискретним масивом зразків $I[p]$, де p — пара цілих індексів. Двовимірний структурний тензор у заданому пікселі зазвичай вважають дискретною сумою

$S_{w}[p]={\begin{bmatrix}\sum _{r}w[r](I_{x}[p-r])^{2}&\sum _{r}w[r]I_{x}[p-r]I_{y}[p-r]\\[10pt]\sum _{r}w[r]I_{x}[p-r]I_{y}[p-r]&\sum _{r}w[r](I_{y}[p-r])^{2}\end{bmatrix}}$

Тут індекс підсумовування r пробігає скінченний набір пар індексів («вікно», зазвичай $\{-m..+m\}\times \{-m..+m\}$ для деякого m), а w[r] — фіксована «віконна вага», яка залежить від r, така, що сума всіх ваг становить 1. Значення $I_{x}[p],I_{y}[p]$ — частинні похідні, взяті в пікселі p; які, наприклад, можна оцінювати з $I$ за формулами скінченних різниць.

Формулу структурного тензора можливо також записати як $S_{w}[p]=\sum _{r}w[r]S_{0}[p-r]$, де $S_{0}$ — матрицезначний масив, такий, що

$S_{0}[p]={\begin{bmatrix}(I_{x}[p])^{2}&I_{x}[p]I_{y}[p]\\[10pt]I_{x}[p]I_{y}[p]&(I_{y}[p])^{2}\end{bmatrix}}$

Інтерпретація

Важливість двовимірного структурного тензора $S_{w}$ випливає з факту узагальнювання власними значеннями $\lambda _{1},\lambda _{2}$ (які можливо впорядковувати так, що $\lambda _{1}\geq \lambda _{2}\geq 0$) та відповідними власними векторами $e_{1},e_{2}$ розподілу градієнта $\nabla I=(I_{x},I_{y})$ функції $I$ у вікні, визначеному $w$ з центром в $p$.

А саме, якщо $\lambda _{1}>\lambda _{2}$, то $e_{1}$ (або $-e_{1}$) — це напрямок, максимально узгоджений із градієнтом у вікні.

Зокрема, якщо $\lambda _{1}>0,\lambda _{2}=0$, то градієнт завжди кратний $e_{1}$ (додатний, від'ємний або нульовий); це справджується тоді й лише тоді, коли $I$ у вікні змінюється вздовж напрямку $e_{1}$, але є сталою вздовж $e_{2}$. Цю умову власних значень також називають умовою лінійної симетрії, оскільки тоді ізолінії $I$ складаються з паралельних прямих, тобто існує одновимірна функція $g$, яка може породжувати двовимірну функцію $I$ як $I(x,y)=g(d^{\text{T}}p)$ для деякого сталого вектора $d=(d_{x},d_{y})^{T}$ та координат $p=(x,y)^{T}$.

З іншого боку, якщо $\lambda _{1}=\lambda _{2}$, то градієнт у вікні не має переважного напрямку; це відбувається, наприклад, коли зображення в цьому вікні має обертову симетрію. Цю умову власних значень також називають збалансованим тілом (англ. balanced body), або умовою напрямкової рівноваги (англ. directional equilibrium), оскільки вона виконується тоді, коли всі напрямки градієнта у вікні однаково часті/імовірні.

Крім того, умова $\lambda _{1}=\lambda _{2}=0$ трапляється тоді й лише тоді, коли функція $I$ в межах $W$ стала ($\nabla I=(0,0)$).

Загальніше, значення $\lambda _{k}$ для k =1 чи k =2 — це $w$-зважене усереднення в околі p квадрата похідної $I$ за напрямком $e_{k}$. Відносна розбіжність між двома власними значеннями $S_{w}$ є покажчиком ступеню анізотропності градієнта у вікні, а саме того, наскільки сильно він схильний до певного напрямку (і його протилежності). Цей атрибут можливо кількісно виразити когере́нтністю (англ. coherence), визначеною як

$c_{w}=\left({\frac {\lambda _{1}-\lambda _{2}}{\lambda _{1}+\lambda _{2}}}\right)^{2}$

якщо $\lambda _{2}>0$. Ця величина дорівнює 1, коли градієнт повністю вирівняний, і 0, якщо він не має переважного напрямку. Формула не визначена, навіть у границі, коли зображення у вікні стале ($\lambda _{1}=\lambda _{2}=0$). Деякі автори визначають її в такому випадку як 0.

Зауважте, що усереднення градієнта $\nabla I$ всередині вікна не є добрим покажчиком анізотропії. Паралельні, але протилежно спрямовані градієнтні вектори в цьому усередненні нейтралізуються, тоді як у структурному тензорі вони належним чином додаються. Ось чому для оптимізації напрямку в усередненні структурного тензора використовують $(\nabla I)(\nabla I)^{\text{T}}$ замість $\nabla I$.

Розширюючи ефективний радіус віконної функції $w$ (тобто, збільшуючи її дисперсію), можливо робити структурний тензор стійкішим до шуму ціною зниження просторової роздільності. Формальну основу цієї властивості описано докладніше нижче, де показано, що багатомасштабне формулювання структурного тензора, яке називають багатомасштабним структурним тензором, становить істинне багатомасштабне подання напрямкових даних за варіацій просторового обширу віконної функції.

Комплексний варіант

Інтерпретація та втілення двовимірного структурного тензора стають особливо доступними за залучення комплексних чисел. Структурний тензор складається з трьох дійсних чисел

$S_{w}(p)={\begin{bmatrix}\mu _{20}&\mu _{11}\\[10pt]\mu _{11}&\mu _{02}\end{bmatrix}}$

де ${\textstyle \mu _{20}=\int (w(r)(I_{x}(p-r))^{2}\,dr}$, ${\textstyle \mu _{02}=\int (w(r)(I_{y}(p-r))^{2}\,dr}$, а ${\textstyle \mu _{11}=\int w(r)I_{x}(p-r)I_{y}(p-r)\,dr}$, де для дискретного подання інтеграли можливо замінити підсумовуваннями. З використанням тотожності Парсеваля стає ясно, що ці три дійсні числа є моментами другого порядку спектрального розподілу енергії $I$. Тоді наступний комплексний момент другого порядку спектрального розподілу енергії $I$ можливо записати як

${\textstyle \kappa _{20}=\mu _{20}-\mu _{02}+i2\mu _{11}=\int (w(r)(I_{x}(p-r)+iI_{y}(p-r))^{2}\,dr=(\lambda _{1}-\lambda _{2})\exp(i2\phi )}$

де $i={\sqrt {-1}}$, $\phi$ — напрямковий кут старшого власного вектора структурного тензора, $\phi =\angle {e_{1}}$, тоді як $\lambda _{1}$ та $\lambda _{2}$ — найбільш і найменш значущі власні значення. З цього випливає, що $\kappa _{20}$ містить як певність (англ. certainty) $|\kappa _{20}|=\lambda _{1}-\lambda _{2}$, так і оптимальний напрямок у подвоєнокутовому поданні, оскільки це комплексне число, що складається з двох дійсних чисел. Звідси також випливає, що якщо градієнт подано комплексним числом, та перевідображено піднесенням до квадрату (тобто, кути аргументу комплексного градієнта подвоєно), то усереднення діє як оптимізатор у цій відображеній області, оскільки воно безпосередньо забезпечує як оптимальний напрямок (у подвоєнокутовому поданні), так і пов'язану з цим певність. Відтак, комплексне число показує, наскільки лінійна структура (лінійна симетрія) присутня в зображенні $I$, а це комплексне число отримують безпосередньо усереднюванням градієнта в його (комплексному) повоєнокутовому поданні без явного обчислення власних значень і власних векторів.

Так само, можливо отримувати наступний комплексний момент другого порядку спектрального розподілу енергії $I$, який завжди дійсний, бо $I$ дійсна,

${\textstyle \kappa _{11}=\mu _{20}+\mu _{02}=\int (w(r)|I_{x}(p-r)+iI_{y}(p-r)|^{2}\,dr=\lambda _{1}+\lambda _{2}}$

де $\lambda _{1}$ та $\lambda _{2}$, як і раніше, — власні значення. Зауважте, що цього разу величину комплексного градієнту піднесено до квадрату (що завжди дійсний).

Проте розкладання структурного тензора на його власні вектори дає його тензорні складові як

$S_{w}(p)=\lambda _{1}e_{1}e_{1}^{\text{T}}+\lambda _{2}e_{2}e_{2}^{\text{T}}=(\lambda _{1}-\lambda _{2})e_{1}e_{1}^{\text{T}}+\lambda _{2}(e_{1}e_{1}^{\text{T}}+e_{2}e_{2}^{\text{T}})=(\lambda _{1}-\lambda _{2})e_{1}e_{1}^{\text{T}}+\lambda _{2}E$

де $E$ — одинична матриця у двох вимірах, оскільки ці два власні вектори завжди перпендикулярні (й дають у сумі одиницю). Перший член у крайньому виразі цього розкладу, $(\lambda _{1}-\lambda _{2})e_{1}e_{1}^{\text{T}}$, подає складову лінійної симетрії структурного тензора, що містить всю напрямкову інформацію (як матриця рангу 1), тоді як другий член подає складову збалансованого тіла тензора, яка не містить жодної інформації про напрямок (містячи одиничну $E$). Тоді знати, скільки напрямкової інформації в $I$, — те саме, що перевіряти, наскільки велика $\lambda _{1}-\lambda _{2}$ порівняно з $\lambda _{2}$.

Очевидно, що $\kappa _{20}$ — комплексний еквівалент першого члена в тензорному розкладі, тоді як

$$(|\kappa _{20}|-\kappa _{11})/2=\lambda _{2}$$

це еквівалент другого члена. Таким чином, ці два скаляри, що складаються з трьох дійсних чисел,

${\begin{array}{c}\kappa _{20}=(\lambda _{1}-\lambda _{2})\exp(i2\phi )&=&w*(h*I)^{2}\\\kappa _{11}=\lambda _{1}+\lambda _{2}&=&w*|h*I|^{2}\\\end{array}}$

де $h(x,y)=(x+iy)\exp(-(x^{2}+y^{2})/(2\sigma ^{2}))$ — (комплексний) градієнтний фільтр, а $*$ — згортка, становлять комплексне подання двовимірного структурного тензора. Як обговорювалося тут і в інших місцях, $w$ визначає локальне зображення, що зазвичай є гауссіаном (з певною дисперсією, що визначає зовнішній масштаб), а $\sigma$ — параметр (внутрішнього масштабу), що визначає ефективний діапазон частот, у якому оцінюють спрямування $2\phi$.

Елегантність комплексного подання випливає з того, що дві складові структурного тензора можливо отримувати як усереднення, і незалежно. Своєю чергою, це означає, що $\kappa _{20}$ та $\kappa _{11}$ можливо використовувати в масштабопросторовому поданні для опису свідчення наявності унікального спрямування та свідчення альтернативної гіпотези, наявності кількох збалансованих спрямувань, без обчислення власних векторів і власних значень. Існування такого функціоналу, як піднесення комплексних чисел у квадрат, для структурних тензорів розмірністю понад два досі показано не було. У Бігуна 91 було заявлено з належною аргументацією, що це через те, що комплексні числа є комутативними алгебрами, тоді як кватерніони, можливий кандидат для побудови такого функціоналу, становлять некомутативну алгебру.

Комплексне подання структурного тензора часто використовують в аналізі відбитків пальців, щоб отримувати карти напрямків, що містять певності, які, своєю чергою, використовують для їхнього покращення, щоби знаходити розташування глобальних (ядра та дельти) та локальних (мінуції) сингулярностей, а також для автоматичного оцінювання якості відбитків.

Тривимірний структурний тензор

Визначення

Структурний тензор можливо визначити також і для функції $I$ трьох змінних p =(x, y, z) абсолютно аналогічним чином. А саме, в безперервному варіанті маємо $S_{w}(p)=\int w(r)S_{0}(p-r)\,dr$, де

$S_{0}(p)={\begin{bmatrix}(I_{x}(p))^{2}&I_{x}(p)I_{y}(p)&I_{x}(p)I_{z}(p)\\[10pt]I_{x}(p)I_{y}(p)&(I_{y}(p))^{2}&I_{y}(p)I_{z}(p)\\[10pt]I_{x}(p)I_{z}(p)&I_{y}(p)I_{z}(p)&(I_{z}(p))^{2}\end{bmatrix}}$

де $I_{x},I_{y},I_{z}$ — три частинні похідні $I$, а інтеграл пробігає $\mathbb {R} ^{3}$.

У дискретному варіанті $S_{w}[p]=\sum _{r}w[r]S_{0}[p-r]$, де

$S_{0}[p]={\begin{bmatrix}(I_{x}[p])^{2}&I_{x}[p]I_{y}[p]&I_{x}[p]I_{z}[p]\\[10pt]I_{x}[p]I_{y}[p]&(I_{y}[p])^{2}&I_{y}[p]I_{z}[p]\\[10pt]I_{x}[p]I_{z}[p]&I_{y}[p]I_{z}[p]&(I_{z}[p])^{2}\end{bmatrix}}$

а сума пробігає скінченну множину тривимірних індексів, зазвичай $\{-m..+m\}\times \{-m..+m\}\times \{-m..+m\}$ для деякого m.

Інтерпретація

Як і у двовимірному випадку, власні значення $\lambda _{1},\lambda _{2},\lambda _{3}$ матриці $S_{w}[p]$ та відповідні власні вектори ${\hat {e}}_{1},{\hat {e}}_{2},{\hat {e}}_{3}$ узагальнюють розподіл напрямків градієнта в околі p, визначеному вікном $w$. Цю інформацію можливо унаочнити як еліпсоїд, півосі якого дорівнюють власним значенням і спрямовані вздовж відповідних власних векторів.

Еліпсоїдне подання тривимірного структурного тензора.

Зокрема, якщо еліпсоїд розтягнуто вздовж лише однієї з осей, як сигару (тобто, якщо $\lambda _{1}$ набагато більше як за $\lambda _{2}$, так і за $\lambda _{3}$), це означає, що градієнт у вікні переважно узгоджується з напрямком $e_{1}$, так, що ізоповерхні $I$ схильні бути пласкими та перпендикулярними до цього вектора. Така ситуація виникає, наприклад, коли p лежить на тонкій пластиноподібній ознаці або на гладкій межі між двома областями з контрастними значеннями.

Еліпсоїд структурного тензора поверхнеподібного околу («серфеля»), де $\lambda _{1}>\!>\lambda _{2}\approx \lambda _{3}$.

Тривимірне вікно, розташоване на гладкій межі між двома рівномірними областями тривимірного зображення.

Відповідний еліпсоїд структурного тензора.

Якщо еліпсоїд сплющено лише в одному напрямку, як млинець (тобто, якщо $\lambda _{3}$ набагато менше як за $\lambda _{1}$, так і за $\lambda _{2}$), це означає, що напрямки градієнта розсіяні, але перпендикулярні $e_{3}$, так, що ізоповерхні схильні бути як труби, паралельні цьому вектору. Така ситуація виникає, наприклад, коли p лежить на тонкій лінієподібній ознаці, або на гострому куті межі між двома областями з контрастними значеннями.

Структурний тензор лінієподібного околу («курвеля», англ. "curvel"), де $\lambda _{1}\approx \lambda _{2}>\!>\lambda _{3}$.

Тривимірне вікно, розташоване на лінієподібній ознаці тривимірного зображення.

Відповідний еліпсоїд структурного тензора.

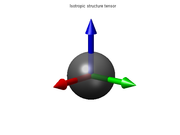
Нарешті, якщо еліпсоїд приблизно сферичний (тобто, якщо $\lambda _{1}\approx \lambda _{2}\approx \lambda _{3}$), це означає, що напрямки градієнта у вікні розподілено більш-менш рівномірно, без явної переваги; так, що функція $I$ в цьому околі переважно ізотропна. Це відбувається, наприклад, коли функція має сферичну симетрію в околі p. Зокрема, якщо еліпсоїд вироджується в точку (тобто, якщо три власні значення дорівнюють нулю), це означає, що $I$ у вікні стала (має нульовий градієнт).

Структурний тензор ізотропного околу, де $\lambda _{1}\approx \lambda _{2}\approx \lambda _{3}$.

Тривимірне вікно, що містить сферичну ознаку тривимірного зображення.

Відповідний еліпсоїд структурного тензора.

Багатомасштабний структурний тензор

Структурний тензор — важливий інструмент у масштабопросторовому аналізі. Багатомасшта́бний структу́рний те́нзор (або багатомасшта́бна ма́триця дру́гого моме́нту, англ. multi-scale structure tensor, multi-scale second moment matrix) функції $I$, на відміну від інших однопараметрових масштабних просторів, демонструє описувач зображення, який визначають двома параметрами масштабу. Один параметр масштабу, який називають локальним масштабом (англ. local scale) $t$, необхідний для визначання рівня попереднього згладжування при обчисленні градієнта зображення $(\nabla I)(x;t)$. Інший параметр масштабу, який називають масштабом інтегрування (англ. integration scale) $s$, необхідний для визначання просторового обширу віконної функції $w(\xi ;s)$, яка визначає ваги для області простору, над якою накопичують складові зовнішнього добутку градієнта на самого себе$(\nabla I)(\nabla I)^{\text{T}}$.

Точніше, припустімо, що $I$ — дійснозначний сигнал, визначений над $\mathbb {R} ^{k}$. Нехай для будь-якого локального масштабу $t>0$ багатомасштабне подання $I(x;t)$ цього сигналу задано через $I(x;t)=h(x;t)*I(x)$, де $h(x;t)$ подає ядро попереднього згладжування. Крім того, нехай $(\nabla I)(x;t)$ позначує градієнт цього масштабопросторового подання. Тоді багатомасштабний структурний тензор/матрицю другого моменту (англ. multi-scale structure tensor/second-moment matrix) визначають через

$\mu (x;t,s)=\int _{\xi \in \mathbb {R} ^{k}}(\nabla I)(x-\xi ;t)\,(\nabla I)^{\text{T}}(x-\xi ;t)\,w(\xi ;s)\,d\xi$

В принципі, можна спитати, чи буде достатньо використовувати будь-які самоподібні сімейства згладжувальних функцій $h(x;t)$ та $w(\xi ;s)$. Проте, якщо наївно застосувати, наприклад, коробковий фільтр, то можуть легко виникнути небажані артефакти. Якщо хотіти, щоби багатомасштабний структурний тензор поводився добре як за зростання локальних масштабів $t$, так і за зростання масштабів інтегрування $s$, то можливо показати, що і функція згладжування, і віконна функція мають бути гауссіанами. Умови, які визначають цю унікальність, подібні до масштабопросторових аксіом, які використовують для виведення унікальності гауссового ядра для звичайного гауссового простору масштабів яскравостей зображення.

У цьому сімействі описувачів зображень існують різні способи оперування двопараметровою мінливістю масштабів. Якщо ми зберігаємо параметр локального масштабу $t$ незмінним, і застосовуємо щодалі розширеніші версії віконної функції, збільшуючи лише параметр масштабу інтегрування $s$, то ми отримуємо істинне формальне масштабопросторове подання напрямкових даних, обчислене у заданому локальному масштабі $t$. Якщо ми пов'яжемо локальний масштаб і масштаб інтегрування відносним масштабом інтегрування (англ. relative integration scale) $r\geq 1$, так, що $s=rt$, то для будь-якого незмінного значення $r$ ми отримуємо зведену самоподібну однопараметрову мінливість, яку часто використовують для спрощення обчислювальних алгоритмів, наприклад, у виявлянні кутів, особливих точок, аналізі текстур, та зіставлянні зображень. Змінюючи відносний масштаб інтегрування $r\geq 1$ у такій самоподібній мінливості масштабу, ми отримуємо інший альтернативний спосіб параметрування багатомасштабної природи напрямкових даних, отримуваних шляхом збільшення масштабу інтегрування.

Концептуально подібну побудову можливо виконати й для дискретних сигналів, замінивши згортковий інтеграл згортковою сумою, а неперервне гауссове ядро $g(x;t)$ — дискретним гауссовим ядром $T(n;t)$:

$\mu (x;t,s)=\sum _{n\in \mathbb {Z} ^{k}}(\nabla I)(x-n;t)\,(\nabla I)^{\text{T}}(x-n;t)\,w(n;s)$

При квантуванні параметрів масштабу $t$ та $s$ у фактичному втіленні зазвичай використовують скінченну геометричну прогресію $\alpha ^{i}$, де i пробігає від 0 до деякого максимального індексу масштабу m. Таким чином, дискретні рівні масштабу матимуть певну подібність до піраміди зображення, хоча просторову підвибірку для збереження точніших даних для наступних етапів обробки можуть використовувати не обов'язково.

Застосування

Власні значення структурного тензора відіграють важливу роль у багатьох алгоритмах обробки зображень, для таких задач як виявляння кутів, особливих точок, та відстежування ознак. Структурний тензор також відіграє центральну роль в алгоритмі оптичного потоку Лукаса — Канаде та в його розширеннях для оцінювання афінного пристосовування форми; де величина $\lambda _{2}$ є показником надійності обчисленого результату. Цей тензор використовували для масштабопросторового аналізу, оцінювання локального спрямування поверхні за монокулярними та бінокулярними сигналами, нелінійного покращування відбитків пальців, дифузної обробки зображень, та кількох інших задач обробки зображень. Структурний тензор також можливо застосовувати в геології для фільтрування сейсмічних даних.

Обробка просторово-часових відеоданих за допомогою структурного тензора

Тривимірний структурний тензор використовували для аналізу тривимірних відеоданих (які розглядали як функцію x, y та часу t). Якщо в цьому контексті націлюватися на описувачі зображення, інваріантні щодо галілеєвих перетворень, щоб уможливити порівняння вимірювань зображення, отримуваних за варіацій апріорно невідомих швидкостей зображення $v=(v_{x},v_{y})^{\text{T}}$

${\begin{bmatrix}x'\\y'\\t'\end{bmatrix}}=G{\begin{bmatrix}x\\y\\t\end{bmatrix}}={\begin{bmatrix}x-v_{x}\,t\\y-v_{y}\,t\\t\end{bmatrix}}$ ,

проте з обчислювальної точки зору краще параметрувати складові в структурному тензорі/матриці другого моменту $S$, використовуючи поняття галілеєвої діагоналізації (англ. Galilean diagonalization)

$S'=R_{\text{space}}^{-{\text{T}}}\,G^{-{\text{T}}}\,S\,G^{-1}\,R_{\text{space}}^{-1}={\begin{bmatrix}\nu _{1}&\,&\,\\\,&\nu _{2}&\,\\\,&\,&\nu _{3}\end{bmatrix}}$

де $G$ позначує галілеєве перетворення простору-часу, а $R_{\text{space}}$ — двовимірне обертання в просторовій області, порівняно з вищезазначеним використанням власних значень тривимірного структурного тензора, що відповідає розкладу на власні значення та (нефізичному) тривимірному обертанню простору-часу

$S''=R_{\text{spacetime}}^{-{\text{T}}}\,S\,R_{\text{spacetime}}^{-1}={\begin{bmatrix}\lambda _{1}&&\\&\lambda _{2}&\\&&\lambda _{3}\end{bmatrix}}$ .

Проте для отримання істинної галілеєвої інваріантності необхідно також пристосовувати форму просторово-часової віконної функції, відповідно до перенесення афінного пристосовування форми з просторових до просторово-часових даних зображення. У поєднанні з локальними просторово-часовими гістограмними описувачами ці концепції разом уможливлюють галілейноінваріантне розпізнавання просторово-часових подій.

Див. також

• Тензор
• Тензорний оператор
• Похідна за напрямком
• Гауссове
• Виявляння кутів
• Виявляння контурів
• Метод Лукаса — Канаде
• Афінне пристосовування форми
• Узагальнений структурний тензор

Ресурси

• Завантажити первинний код MATLAB
• Посібник зі структурних тензорів (оригінал) (англ.)