Теорема Александрова про розгортку

Теорема Александрова про розгортку — теорема про єдиність замкнутого опуклого багатогранника з даною розгорткою, доведена Олександром Даниловичем Александровим. Є узагальненням теореми Коші про багатогранники і має схоже доведення.

Узагальнення цієї теореми на довільні метрики на сфері зіграло ключову роль у становленні та розвитку Александровської геометрії.

Формулювання

Багатогранна метрика на сфері ізометрична поверхні опуклого багатогранника тоді і тільки тоді, коли сума кутів при будь-якій її вершині не перевершує $2{\cdot }\pi$. Більше того, багатогранник визначається метрикою на своїй поверхні з точністю до конгруентності.

При цьому допускається, що багатогранник вироджується у плоский багатокутник, у цьому випадку поверхня багатогранника визначається як подвоєння багатокутника в його межі, тобто дві копії багатокутника склеєні у відповідних точках межі.

Зауваження

Розгортка октаедра з чотирьох шестикутників.

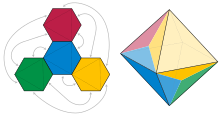
• В оригінальному формулюванні Александров користується поняттям розгортки багатогранника на площині, тобто набору плоских багатокутників і правил склеювання цих багатокутників у багатогранну метрику. Одну з таких розгорток можна отримати з набору всіх граней багатогранника з природним правилом склеювання. Проте в загальному випадку, багатокутники розгортки можуть перекриватися з кількома гранями (дивись малюнок).

Варіації та узагальнення

• (Теорема Александрова) Внутрішня метрика на сфері ізометрична поверхні опуклого тіла тоді і тільки тоді, коли вона має невід'ємну кривину в сенсі Александрова. При цьому допускається, що тіло вироджується у плоску фігуру, у цьому випадку поверхня фігури визначається як її подвоєння.
  • (Теорема Погорєлова) Більше того, опукле тіло визначається однозначно з точністю до конгруентності.
  • (Теорема Оловянишнікова) Повна метрика $d$ на площині $\mathbb {R} ^{2}$ ізометрична поверхні опуклої множини $K\subset \mathbb {R} ^{3}$ тільки тоді, коли вона має невід'ємну кривину в сенсі Александрова. Більше того, конус на нескінченності $K$можна задати довільно за умови, що його межа ізометрична конусу на нескінченності $(\mathbb {R} ^{2},d)$.

Див. також

• Теорема монотонності Александрова
• Список об'єктів, названих на честь Олександра Александрова