Доповнення множин

Теоретико-множинні операції

${\overline {A}}\!$ доповнення

$A\cup B\!$ об'єднання
$A\cap B\!$ перетин

$A\setminus B\!$ різниця

$A\triangle B\!$ симетрична різниця
$A\times B\!$ декартів добуток

В теорії множин та інших галузях математики, одна з основних операцій на множинах.

Розрізняють доповнення множин (абсолютне доповнення) та різницю множин (відносне доповнення).

Різниця множин (відносне доповнення)

Якщо A та B - множини, то різницею між B та А (порядок множин важливий), або відносним доповненням A до B, є множина з елементів B, які не належать A. Різниця множин є бінарною операцією.

Відносне доповнення A до B:
$B\setminus A~~~=~~~A^{c}\cap B$

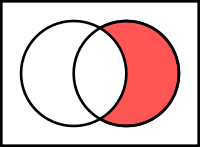
Відносне доповнення A до B позначається як B − A (також B \ A).

Формально:

$B-A=\{x\,|\,x\in B\,\wedge \,x\not \in A\}$

Приклади:

• {1,2,3} − {2,3,4}   =   {1}
• {2,3,4} − {1,2,3}   =   {4}
• Якщо $\mathbb {R}$ - множина дійсних чисел, і $\mathbb {Q}$ - множина всіх раціональних чисел то $\mathbb {R} -\mathbb {Q}$ є множиною ірраціональних чисел.

Наступне твердження містить основні властивості операції різниці множин та її співвідношення з операціями об'єднання та перетину множин

ТВЕРДЖЕННЯ 1: Якщо A, B, та C є множини, то справедливі наступні співвідношення::

• C − (A ∩B)  =  (C − A) ∪(C − B)
• C − (A ∪B)  =  (C − A) ∩(C − B)
• C − (B − A)  =  (A ∩C) ∪(C − B)
• (B − A) ∩C  =  (B ∩C) − A  =  B ∩(C − A)
• (B − A) ∪C  =  (B ∪C) − (A − C)
• A − A  =  Ø
• Ø − A  =  Ø
• A − Ø  =  A

Абсолютне доповнення

Доповнення A до U
$A^{c}~~~=~~~U\setminus A$

Для універсальної множини U, відносне доповнення деякої множини A до U називається абсолютним доповнення (або просто доповненням) A, і позначається як A^C або C_A:

A^C  =  U − A

Наступне твердження містить деякі основні властивості абсолютного доповнення та зв'язок цієї операції з операціями об'єднання та перетину множин

ТВЕРДЖЕННЯ 2: Якщо A та B є підмножини U, то виконуються наступні співвідношення:

правила де Моргана:

• (A ∪B)^C  =  A^C ∩B^C
• (A ∩B)^C  =  A^C ∪B^C

закони доповнення:

• A ∪A^C   =  U
• A ∩A^C  =  Ø
• Ø^C  =  U
• U^C  =  Ø

закон подвійного доповнення (операція доповнення є інволюцією):

• A^CC  =  A.

Попереднє співвідношення твердить, що якщо A є непорожня підмножина U, то {A, A^C } є поділом U.