Терм (логіка)
У математичній логіці терм позначає математичний об'єкт, у той час як формула[en] позначає математичний факт. Зокрема, терми виступають як компоненти формули. Це аналогічно звичайній мові, де іменник відноситься до об'єкта, а ціле речення відноситься до факту.
Терм першого порядку рекурсивно будується з константних символів, змінних і функціональних символів[en]. Вираз, утворений застосуванням предикатного символу до відповідної кількості термів, називається атомарною формулою[en], яка оцінюється як істинна чи хибна в бівалентній логіці, за умови інтерпретації. Наприклад, — це терм, побудований з константи 1, змінної x і символів бінарної функції і ; це частина атомної формули яка оцінюється як істина для кожного дійсного значення x.
Окрім логіки, терми відіграють важливу роль в універсальній алгебрі та системах рерайтингу.
Формальне визначення[ред. | ред. код]
Дано набір V змінних символів, набір C постійних символів і набори Fn з n-арних функціональних символів, які також називають символами операторів, для кожного натурального числа n ≥ 1, набір несортованих термів першого порядку T, рекурсивно визначений як найменший набір з такими властивостями:[1]
- кожен символ змінної є термом: V ⊆ T ,
- кожен постійний символ є термом: C ⊆ T,
- з кожних n термів t1,…,tn, і кожного n-арного символу функції f ∈ Fn, можна побудувати більший терм f(t1,…,tn).
Використовуючи інтуїтивну, псевдограматичну нотацію, описані вище правила іноді записують так: t ::= х | c | f (t1, …, tn). Зазвичай використовують лише перші декілька наборів функціональних символів Fn . Добре відомими прикладами є символи унарних функцій sin, cos ∈ F1 та символи бінарних функцій +, −, ⋅, / ∈ F2, тоді як тернарні операції менш відомі, не кажучи вже про функції вищої арності. Багато авторів розглядають константні символи як 0-арні функціональні символи F0, тому для них не потрібно спеціального синтаксичного класу.
Термом позначають математичний об'єкт з області дискурсу. Константа c позначає іменований об'єкт з цього домену, змінна x охоплює об'єкти у цьому домені, а n-арна функція f відображає кортежі з n елементів об'єктів на об'єкти. Наприклад, якщо n ∈ V — змінний символ, 1 ∈ C — константний символ, та add ∈ F2 — символ бінарної функції, то n ∈ T, 1 ∈ T, а отже, add(n, 1) ∈ T відповідно до першого, другого та третього правила побудови терма. Останній терм зазвичай записується як n+1 з використанням інфіксної нотації та більш поширеного оператора + для зручності.
Структура Терма та його представлення[ред. | ред. код]
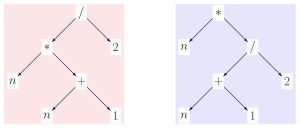
Спочатку, логіки визначали терм як рядок символів, що дотримується певних правил побудови.[2] Однак, оскільки концепція дерева стала популярною в інформатиці, виявилося, що більш зручно вважати терм деревом. Наприклад, кілька окремих рядків символів, як "(n⋅(n+1))/2 ", та "((n⋅(n+1)))/2 ", і «», позначають той самий терм і відповідають тому самому дереву, а саме лівому дереву на малюнку вище. Відокремлюючи структуру терма (деревоподібну) від його графічного представлення на папері, також легко врахувати дужки та невидимі оператори множення(вони існують лише в структурі, та їх нема у представленні).
Структурна рівність[ред. | ред. код]
Два терми називаються структурно, буквально або синтаксично рівними, якщо вони є представленням одного й того ж синтаксичного дерева. Наприклад, ліве і праве дерево на наведеному вище малюнку є структурно нерівними термами, хоча їх можна вважати «семантично рівними», оскільки вони завжди мають однакове значення в раціональній арифметиці. Хоча структурну рівність можна перевірити без будь-яких знань про значення символів, перевірити таким чином семантичну рівність неможливо. Якщо функція /, наприклад, інтерпретується не як раціональна, а як усікаюче ціле ділення, то при n=2, лівий та правий члени дорівнюють 3 і 2 відповідно. Структурно рівні терми повинні узгоджуватися в іменах змінних.
Навпаки, терм t називається перейменуванням або варіантом терма u, якщо терм u є результатом послідовного перейменування всіх змінних терма t, тобто якщо u = tσ для деякої заміни[en]перейменування σ. У цьому випадку u також є перейменуванням t, оскільки заміна перейменування σ має обернене значення σ−1, а t = uσ−1. Тоді обидва терми також називаються рівними за модулем перейменування. У багатьох контекстах конкретні назви змінних у термі не мають значення, наприклад, аксіому комутативності для додавання можна сформулювати як «x + y = y + x» або як «a + b = b + a»; у таких випадках вся формула може бути перейменована, тоді як довільний підтерм формули зазвичай не може бути перейменованим, наприклад, «x + y = b + a» не є вірним варіантом аксіоми комутативності.[note 1][note 2]
Замкнені та лінійні терми[ред. | ред. код]
Множину змінних терма t позначають vars(t). Терм, який не містить змінних, називається замкненим термом; терм, який не містить багаторазових зустрічей змінної, називається лінійним термом. Наприклад, 2+2 є замкненим термом, а отже, також і лінійним, x⋅(n+1) є лінійним термом, n⋅(n+1) є нелінійним термом. Ці властивості важливі, наприклад, при рерайтенгу термів .
З огляду на сигнатуру функціональних символів, множина всіх термів утворює вільну[en] алгебру термів[en]. Множина всіх замкнених термів утворює початкову алгебру термів.
Скорочуючи кількість констант як f0, а кількість символів i-нарной функції як fi, число θh різних замкнених термів висоти(дерева) до h може бути обчислено за такою формулою рекурсії:
- θ0 = f0, оскільки замкнений терм висоти 0 може бути лише константою,
- , оскільки замкнений терм висотою до h+1 можна отримати шляхом складання будь-яких i замкнених термів висотою до h, використовуючи i-арний кореневий символ функції. Сума має кінцеве значення, якщо існує лише скінченна кількість констант і символів функцій, що зазвичай буває.
Побудова формул із термів[ред. | ред. код]
Припустимо маємо набір Rn з n-арних символів для кожного натурального числа n ≥ 1, атомарна несортована формула першого порядку отримується шляхом застосування n-арного символу ставлення до n термів. Що стосується функціональних символів, набір символів відносини Rn зазвичай непорожній тільки для малих n. В математичній логіці більш складні формули будуються з атомарних формул з використанням логічних сполучників і кванторів. Наприклад, нехай яка позначає набір дійсних чисел, ∀x: x ∈ ⇒ (x+1)⋅(x+1) ≥ 0 — це математична формула, яка оцінюється як істинна(«True») в алгебрі комплексних чисел. Атомарна формула називається замкненою, якщо вона повністю побудована з основних термів; всі основні атомарні формули, складені з заданого набору функцій і предикатів, складають базу Гербранда[en] для цих наборів символів.
Операції з термами[ред. | ред. код]

- Оскільки терм має структуру дерева, кожному з його вузлів може бути присвоєна позиція або шлях, тобто рядок натуральних чисел, що вказує місце вузла в ієрархії. Порожній рядок, зазвичай позначається ε, та присвоюється кореневому вузлу. Рядки положення всередині чорного терма позначені на малюнку червоним кольором.
- В кожній позиції p терма t починається унікальний підтерм, який зазвичай позначається t|p. Наприклад, в позиції 122 чорного терма на малюнку, підтерм a+2 має свій корінь. Відношення «є підтермом» — це частковий порядок у наборі термів; він рефлексивний, оскільки кожен терм тривіально є підтермом самого себе.
- Терм, отриманий шляхом заміни в термі t підтерма в позиції p новим термом u, зазвичай позначається t[u]p. Терм t[u]p також можна розглядати як результат узагальненої конкатенації терма u з об'єктом, подібним до терма t[.]; останній називається контекстом або відкритим термом(позначати «.»; його позиція дорівнює p), в якому кажуть, що u вбудований. Наприклад, якщо t — чорний терм на малюнку, то t[b+1]12 призводить до терма . Останній терм також є результатом вбудовування терма b+1 у контекст . У неофіційному сенсі операції створення екземплярів[en] та операція вбудовування протилежні одна одній: в той час як перша додає функціональні символи в нижній частині терма, друга додає їх вгорі. Порядок охоплення[en] пов'язує терм і результат додавання з обох сторін.
- Кожному вузлу терма може бути присвоєна його глибина (називається деякими авторами висота), тобто його відстань (кількість ребер) від кореня. У цьому параметрі глибина вузла завжди дорівнює довжині рядка його позиції. На малюнку рівні глибини в чорному терміні позначені зеленим кольором.
- Розмір терма зазвичай відноситься до числа його вузлів або, що еквівалентно, до довжини письмового подання терма, вважаючи символи без круглих дужок. Чорний і синій терми на зображенні мають розмір 15 і 5 відповідно.
- Терм u відповідє терму t, якщо екземпляр заміщення u структурно дорівнює вкладеному терму t, або формально, якщо uσ = t|p для деякої позиції p в t і деякої заміни σ. В цьому випадку u, t і σ називаються шаблонним термом, суб'єктним термом і відповідною заміною відповідно. На зображенні синій шаблон відповідає чорному предметному терму в позиції 1, з відповідною заміною{ x ↦ a, y ↦ a+1, z ↦ a+2 }, позначеної синіми змінними, відразу залишеними для їх чорних замінників. Інтуїтивно зрозуміло, що шаблон, за винятком його змінних, повинен міститися в суб'єкти; якщо змінна зустрічається в шаблоні кілька разів, у відповідних позиціях суб'єкта потрібні рівні проміжні умови.
- об'єднуючі терми
- рерайтинг терма
Пов'язані поняття[ред. | ред. код]
Відсортовані терми[ред. | ред. код]
Коли область дискурсу містить елементи принципово різних типів, корисно відповідним чином розділити набір всіх термів. З цією метою кожній змінній та кожній константі присвоюється сортування(іноді також називається тип), а кожному функціональному символу присвоюється[note 3] сортування домену та сортування за діапазоном. Відсортований терм f(t1,…,tn) може бути складений з відсортованих вкладених термів t1,…,tn тільки в тому випадку, якщо сортування і-го підтерма відповідає оголошеному i-му виду домену f. Такий терм також називається добре відсортованим; будь-який інший терм(тобто в якому виконуються тільки несортовані правила) називають погано відсортованим.
Наприклад, векторний простір має пов'язане з ним з поле скалярних чисел. Нехай W і N позначають сортування векторів і чисел відповідно,VW і VN — множина векторних і числових змінних відповідно, а CW і CN — множина векторних і числових констант відповідно. Тоді і 0 ∈ CN, а векторне додавання, скалярне множення та внутрішній добуток оголошуються як відповідно. Припускаючи, що змінні символи та , тоді терм є добре відсортованим, проте не є добре відсортованим(оскільки + не приймає терм типу N як 2-й аргумент). Для того, щоб зробити добре відсортованим, необхідно додати ще одне визначення: . Функціональні сімволи, які мають кілька декларацій, називаються перевантаженими .
Лямбда терми[ред. | ред. код]
| Приклад позначення | Зв'язані змінні | Вільні змінні | Записано у вигляді лямбда-терму |
|---|---|---|---|
| n | x | limit(λn. div(x,n)) | |
| i | n | sum(1,n,λi. power(i,2)) | |
| t | a, b, k | integral(a,b,λt. sin(k⋅t)) |
Мотивація[ред. | ред. код]
Математичні позначення, як показано в таблиці, не вписуються в схему терма першого порядку, як визначено вище, оскільки всі вони вводять власну локальну або обмежену змінну, яка може не відображатися за межами нотації, наприклад не має сенсу. На противагу цьому, інші змінні, які називаються вільними, поводяться як звичайні змінні першого порядку, наприклад .
Усі ці оператори можна розглядати як один із аргументів функції, а не значення терму. Наприклад, оператор lim застосовується до послідовності, тобто до відображення з натурального цілого в, наприклад, дійсні числа. Як інший приклад, функція C для реалізації другого прикладу з таблиці, Σ, матиме аргумент вказівника функції.
Лямбда-терми можна використовувати для позначення анонімних функцій, які надаються як аргументи для lim, Σ, ∫ тощо.
Наприклад, функція піднесеня числа до квадрату з програми C нижче можна записати анонімно як лямбда-терм λi. і2. Тоді загальний оператор суми Σ можна розглядати як тернарний символ потрійної функції, що приймає значення нижньої границі, значення верхньої границі та функцію, яку потрібно підсумувати. Завдяки своєму останньому аргументу оператор Σ називається символом функції другого порядку. Як інший приклад, лямбда-терм λn. x / n позначає функцію, яка відображає 1, 2, 3, … у x/1, x/2, x/3, … відповідно, тобто позначає послідовність (x/1, x/2, x/3, …). Оператор lim приймає таку послідовність і повертає її границю (якщо вона визначена).
Крайній правий стовпець таблиці вказує, як кожен приклад математичної нотації може бути представлений у вигляді лямбда-терму, також записані звичайні інфіксні оператори в префіксну форму.
int sum(int lwb, int upb, int fct(int)) { // implements general sum operator
int res = 0;
for (int i=lwb; i<=upb; ++i)
res += fct(i);
return res;
}
int square(int i) { return i*i; } // implements anonymous function (lambda i. i*i); however, C requires a name for it
#include <stdio.h>
int main(void) {
int n;
scanf(" %d",&n);
printf("%d\n", sum(1, n, square)); // applies sum operator to sum up squares
return 0;
}
Примітки[ред. | ред. код]
- ↑ Оскільки атомарні формули також можна розглядати як дерева, а перейменування, по суті, є концепцією дерев, атомарність (і, в більш загальному вигляді, без кванторів) формули можна перейменувати так само, як і терми. Фактично, деякі автори розглядають формулу без кванторів як терм (типу bool, а ні наприклад int).
- ↑ Перейменування аксіоми комутативності можна розглядати як альфа-перетворення в універсальне закриття аксіоми: «x+y=y+x» що насправі є «∀x,y: x+y=y+x», що є синонімом до «∀a,b: a+b=b+a».
- ↑ Тобто «тип символу» в розділі багатосортованих сигнатур у статті Сигнатура(логіка).
Див. також[ред. | ред. код]
Посилання[ред. | ред. код]
- Franz Baader; Tobias Nipkow (1999). Term Rewriting and All That. Cambridge University Press. с. 1–2 and 34–35. ISBN 978-0-521-77920-3.
- ↑ C.C. Chang; H. Jerome Keisler (1977). Model Theory. Studies in Logic and the Foundation of Mathematics. Т. 73. North Holland.; here: Sect.1.3
- ↑ Hermes, Hans (1973). Introduction to Mathematical Logic. Springer London. ISBN 3540058192. ISSN 1431-4657.; here: Sect.II.1.3
| |||||||||||||||||||||||||||||||||||||||||||||||||
























