Теорема Піка: відмінності між версіями
| [неперевірена версія] | [неперевірена версія] |
Немає опису редагування |
Немає опису редагування Мітки: перше редагування Перемкнуто з візуального редактора |
||
| Рядок 1: | Рядок 1: | ||
[[Файл:Pick theorem.svg|thumb|250px|right|Многокутник із цілочисловими вершинами.]] |
|||
'''Теорема Піка''' — класичний результат в [[комбінаторна геометрія|комбінаторній геометрії]] і [[геометрія чисел|геометрії чисел]]. |
|||
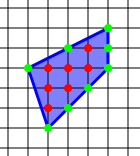
[[File:Pick-theorem.png|right|thumb|{{color|red|{{math|''i'' {{=}} 7}}}}, {{color|green|{{math|''b'' {{=}} 8}}}}, {{math|''S'' {{=}} {{color|red|''i''}} + {{sfrac|{{color|green|''b''}}|2}} − 1 {{=}} 10}}]] |
|||
[[Площа]] [[многокутник]]а з цілочисловими вершинами рівна сумі |
|||
[[Image:coprime-lattice.svg|thumb|right|300px| Трикутник з вершинами в нижній лівій, нижній правій, та верхній правій точках {{math|''i'' {{=}} 12}} та {{math|''b'' {{=}} 14}}, відповідно до теореми Піка {{math|''S'' {{=}} ''i'' + {{sfrac|''b''|2}} − 1 {{=}} 18}}; це підтверджує формулі площі для трикутника {{nowrap|{{sfrac|1|2}} × основа × висота}} = {{nowrap|{{sfrac|1|2}} × 9 × 4}} = 18.]] |
|||
: <math>A = i + \frac{b}{2} - 1.</math> |
|||
де ''i'' — кількість цілочислових точок усередині многокутника, ''b'' — кількість цілочислових точок на межі многокутника. |
|||
''Див. також теорему в комплексному аналізі див. {{не перекладено|Лемма Шварца, теорема Шварца—Піка|Лемма Шварца, теорема Шварца—Піка|en|Schwarz_lemma#Schwarz-Pick_theorem}}. |
|||
Точка координатної площини називається цілочисловою якщо обидві її координати [[ціле число|цілі числа]]. |
|||
Якщо розглянути [[простий багатокутник]], |
|||
В прикладі на малюнку i = 39; b = 14; отже площа рівна A = 39 + 14/2 − 1 = 39 + 7 − 1 = 45 (квадратних одиниць). |
|||
побудований на сітці рівновіддалених точок (тобто точок з {{не перекладено|цілими|цілі|en|Integer}} координатами), так, що всі вершини багатокутника є точками сітки, '''теорема Піка''' дає просту формулу |
|||
для обчислення [[площі]] |
|||
{{mvar|S}} цього многокутника, за кількістю {{mvar|i}} (точок решітки усередині фігури) і кількістю {{mvar|b}} (точок решітки), розміщених по периметру многокутника:<ref>{{cite journal |last=Trainin |first=J. |title=An elementary proof of Pick's theorem |journal={{не перекладено|Mathematical Gazette|Mathematical Gazette|en|The_Mathematical_Gazette}} |volume=91 |issue=522 |date=November 2007 |pages=536–540|doi=10.1017/S0025557200182270 }}</ref> |
|||
:<math>S = i + \frac{b}{2} - 1.</math> |
|||
Зокрема, площа трикутника з вершинами у вузлах, що не містить вузлів ні всередині, ні на сторонах (окрім вершин), рівна 1/2. |
|||
Цей факт дає геометричні доказ формули для різниці відповідних дробів [[ланцюгові дроби|ланцюгового дробу ]]. |
|||
У наведеному прикладі маємо {{math|''i'' {{=}} 7}} (внутрішніх точок) і {{math|''b'' {{=}} 8}} (граничних точок), так що площа {{mvar|A}} = 7 + {{sfrac|8|2}} − 1 = 7 + 4 − 1 = 10 квадратних одиниць. |
|||
== Історія == |
|||
Вищенаведена теорема справедлива лише для простих багатокутників, тобто для тих, які складаються з єдиної непересічної межі, без дірок. Для загального многокутника ''формула Піка'' має такий вигляд:<ref name=":0">{{Cite web|url=https://documents.kenyon.edu/math/GarbettJSenEx2011.pdf|title=Lattice Point Geometry: Pick's Theorem and Minkowski's Theorem, Senior Exercise in Mathematics|last=Garbett|first=Jennifer|date=November 18, 2010|archive-url=https://web.archive.org/web/20170829044759/http://documents.kenyon.edu/math/GarbettJSenEx2011.pdf|archive-date=29 Aug 2017|url-status=}}</ref><ref>{{Cite journal|last=Belyaev|first=Alexander|last2=Fayolle|first2=Pierre-Alain|date=2019-08-08|title=Counting Parallel Segments: New Variants of Pick's Area Theorem|journal=The Mathematical Intelligencer|volume=41|issue=4|pages=1–7|language=en|doi=10.1007/s00283-019-09921-8|issn=0343-6993}}</ref> |
|||
:<math>S = v - \frac 1 2 e_b + h - 1</math> |
|||
де <math>v</math> - кількість вершин всередині і на межі многокутника, <math>e_b</math> - кількість точок решітки на межі многокутника, і <math>h</math> - кількість дірок у многокутнику. |
|||
Як приклад розглянемо ''багатокутник'', побудованний за допомогою |
|||
точок <math>(0, 0), (2, 0)</math>. Він має 3 вершини, 0 отворів і 0 область. Щоб формула працювала, повинно бути 4 ребра. Таким чином, треба просто порахувати кожен край двічі, ''один раз на кожній стороні''. |
|||
Результат вперше описав [[Георг Александр Пік]] в [[1899]].<ref>{{cite journal |last=Pick |first=Georg |title=Geometrisches zur Zahlenlehre |journal=Sitzungsberichte des deutschen naturwissenschaftlich-medicinischen Vereines für Böhmen "Lotos" in Prag |series=(Neue Folge) |year=1899 |volume=19 |pages=311–319 |url=https://www.biodiversitylibrary.org/item/50207#page/327 |JFM=33.0216.01 }} [http://citebank.org/node/47270 CiteBank:47270]</ref> {{не перекладено|Тетраедр Ріва|Тетраедр Ріва|en|Reeve_tetrahedron}} демонструє, що немає аналоги теореми Піка в розмірності три, яка виражає об'єм багатогранника через кількість внутрішніх і граничних точок. Однак є узагальнення для високих розмірностей через {{не перекладено|многочлени Ерхарта|многочлени Ерхарта|en|Ehrhart_polynomial}}. |
|||
Формула Піка була відкрита австрійським математиком [[Георг Александр Піка|Георгом Александером Піком]] в [[1899]] році. |
|||
== Доведення == |
== Доведення == |
||
Розглянемо багатокутник {{mvar|P}} і трикутник {{mvar|T}}, що має з {{mvar|P}} одне спільне ребро. Припустимо, що теорема Піка справедлива як для {{mvar|P}}, так і для {{mvar|T}} незалежно один від одного; ми хочемо показати, що це також справедливо для багатокутника {{mvar|PT}}, отриманого шляхом додавання {{mvar|T}} до {{mvar|P}}. Оскільки {{mvar|P}} і {{mvar|T}} маю одне спільне ребро, всі граничні точки уздовж цього ребра стають внутрішніми точками, за винятком двох кінцевих точок, які об'єднуються з граничними точками. Отже, якщо <math>C</math> кількість спільних граничних точок, то маємо<ref>{{cite book|last1=Beck|first1=Matthias|last2=Robins|first2=Sinai|date=2007|title=Computing the Continuous Discretely: Integer-point enumeration in polyhedra|series=[[Undergraduate Texts in Mathematics]]|location=New York|publisher=Springer-Verlag|isbn=978-0-387-29139-0}}</ref> |
|||
У даному доведенні всі многокутники задовольняють умову теореми тобто мають цілочислові вершини. |
|||
:<math>i_{PT} = i_P + i_T + (c - 2)</math> |
|||
Нехай ''P'' — деякий многокутник і [[трикутник]] ''T'', має одну сторону спільну з ''P''. Припустимо, що для ''P'' теорема виконується; доведемо, що вона також виконується для многокутника ''PT'' одержаного приєднанням ''T'' до ''P''. Оскільки ''P'' і ''T'' мають спільну сторону, всі граничні точки на цій стороні об'єднуються у внутрішні точки, за винятком двох кінців даної сторони, що стають граничними точками. Тому якщо кількість спільних граничних точок рівна ''c'', то виконується |
|||
і |
|||
: <math>i_{PT} = (i_P + i_T) + (c - 2)\,</math> |
|||
:<math>b_{PT} = b_P + b_T - 2(c - 2) - 2.</math> |
|||
З вищезазначеного випливає |
|||
:<math>i_P + i_T = i_{PT} - (c - 2)</math> |
|||
і |
і |
||
: |
:<math>b_P + b_T = b_{PT} + 2(c - 2) + 2.</math> |
||
Оскільки ми припускаємо виконання теореми і для {{mvar|P}} і для {{mvar|T}}, то |
|||
Звідси |
|||
: <math>\begin{align} |
|||
: <math>(i_P + i_T) = i_{PT} - (c - 2)\,</math> |
|||
S_{PT} &= S_P + S_T\\ |
|||
&= \left(i_P + \frac{b_P}{2} - 1\right) + \left(i_T + \frac{b_T}{2} - 1\right)\\ |
|||
&= i_P + i_T + \frac{b_P + b_T}{2} - 2\\ |
|||
&= i_{PT} - (c - 2) + \frac{b_{PT} + 2(c - 2) + 2}{2} - 2\\ |
|||
&= i_{PT} + \frac{b_{PT}}{2} - 1. |
|||
\end{align}</math> |
|||
Тому, якщо теорема справедлива для многокутників побудованих з {{mvar|n}} трикутників, вона справедлива і для многокутників, що побудовані з {{math|''n'' + 1}}трикутника. Добре відомо, що довільний [[многокутник]] можна розбити на симплекси [[триангуляція]]. |
|||
і |
|||
Це тривіальний факт у випадку площини. |
|||
Для завершення доведення методом {{не перекладено|математичної індукції|математична індукція|en|Mathematical_induction}} достатньо довести її у випадку трикутників. |
|||
Перевірку цього випадку здійснюється за допомогою наступних коротких кроків: |
|||
* припускаємо, що формула справедлива для будь-якого {{не перекладено|одиничного квадрата|одиничний квадрат|en|Unit_square}} (з вершинами, що мають цілі координати); |
|||
* на основі цього виводимо, що формула є справедливою для будь-якого {{не перекладено|прямокутника|прямокутник|en|Rectangle}} зі сторонами парелельними осям; |
|||
* отримуємо формулу для прямокутних трикутників, отриманих шляхом розрізання таких прямокутників по {{не перекладено|діагоналі|діагональ|en|Diagonal}}; |
|||
* тепер будь-який трикутник можна перетворити на прямокутник, приєднавши такі прямокутні трикутники; оскільки формула виконується для прямокутних трикутників і для прямокутника, вона також буде виконуватися для початкового трикутника. |
|||
На останньому кроці застосовується той факт, що якщо теорема справедлива для багатокутника {{mvar|PT}} і для трикутника {{mvar|T}}, то це також має місце для багатокутника {{mvar|P}}; це можна побачити на основі обчислень, які подібні до наведених вище. |
|||
== Нерівність для опуклих множин == |
|||
Нехай <math>C</math> — обмежена, опукла область в <math>\mathbb R^2</math>, не обов'язково замкнена. Тоді |
|||
<math>|L(C)| \le \text{площа}(C) + \frac 1 2 \text{периметр}(C) + 1</math>.<ref name=":0" /> |
|||
де <math>L(C)</math> — це набір точок решітки в <math>C</math>, і <math>|L(C)|</math> — їх кількість. Рівність має місце тоді і лише тоді, коли <math>C</math> — замкнений багатокутник решітки. |
|||
Для доведення розглянемо опуклий оболонку <math>\bar{C}</math> для <math>L(C)</math>, яку слід розуміти як наближення решітки для області <math>C</math>, а потім застосуємо до неї '''теорему Піка''': |
|||
: <math>\begin{align} |
|||
|L(C)| = |L(\bar C)| &= \text{площа}(\bar C) + \frac 1 2 B(\bar C) + 1 \\ |
|||
&\le \text{площа}(\bar C) + \frac 1 2 \text{периметр}(\bar C) + 1 |
|||
\\ |
|||
&\le \text{площа}(C) + \frac 1 2 \text{периметр}(C) + 1 |
|||
\end{align} </math> |
|||
де <math>B(\bar C)</math> — кількість граничних точок <math>\bar{C}</math>, що дорівнює кількості його ребер, і оскільки кожне ребро має мінімальну довжину 1, то |
|||
<math>B(\bar C)\le \text{периметр}(\bar C)</math> |
|||
Перехід ''<math>\text{периметр}(\bar C) \le \text{периметр}(C)</math>'' використовує властивість, що між двома вкладеними, опуклими, замкнутими кривими, внутрішня крива буде коротшою на основі прямого застосування {{не перекладено|формули Крофтона|формули Крофтона|en|Crofton_formula#Applications}}. |
|||
Формула залишається справедливою і у виродженому випадку, коли <math>L(C)</math> знаходиться на одній лінії. Потрібно просто порахувати кожен ребро двічі (по одному разу з кожної сторони). |
|||
== Див. також == |
|||
*{{не перекладено|Цілі точки в опуклих багатогранниках|Цілі точки в опуклих багатогранниках|en|Цілі точки в опуклих багатогранниках}} |
|||
*{{не перекладено|довгомір Штайнгауза|довгомір Штайнгауза|en|довгомір Штайнгауза}} |
|||
*{{не перекладено|Послідовність Фарі|Послідовність Фарі|en|Послідовність Фарі}} |
|||
: <math>(b_P + b_T) = b_{PT} + 2(c - 2) + 2.\,</math> |
|||
== Список літератури == |
|||
Якщо теорема виконується для ''P'' і ''T'' то, |
|||
: <math> |
|||
\begin{align} |
|||
A_{PT} &= A_P + A_T\\ |
|||
&= (i_P + b_P/2 - 1) + (i_T + b_T/2 - 1)\\ |
|||
&= (i_P + i_T) + (b_P + b_T)/2 - 2\\ |
|||
&= i_{PT} - (c - 2) + (b_{PT} + 2(c - 2) + 2)/2 - 2\\ |
|||
&= i_{PT} + b_{PT}/2 - 1. |
|||
\end{align} |
|||
</math> |
|||
Тому, якщо теорема справедлива для многокутників, що одержуються подібним чином з ''n'' трикутників, вона справедлива і для многокутників, що одержуються з ''n'' + 1 трикутника. Оскільки для довільного многокутника існує подібна [[триангуляція]] для доведення теореми достатньо довести її у випадку трикутників і скористатися [[метод математичної індукції|методом математичної індукції]]. |
|||
Доведення теореми для трикутників здійснюється за наступною схемою: |
|||
* формула справедлива для одиничного [[квадрат]]а; |
|||
* звідси випливає справедливість для [[прямокутник]]ів сторони яких [[паралельність|паралельні]] осям; |
|||
* з попереднього неважко довести теорему для [[прямокутний трикутник|прямокутних трикутників]], [[катет]]и яких паралельні осям; |
|||
* довільний трикутник може за допомогою щонайбільше трьох прямокутних трикутників бути доповнений до прямокутника і з виконання теореми для прямокутників і прямокутних трикутників випливає справедливість теореми для довільних трикутників. |
|||
== Посилання == |
|||
* Weisstein, Eric W., [http://mathworld.wolfram.com/PicksTheorem.html «Pick's Theorem»] from MathWorld. |
|||
* В. В. Прасолов Задачи по планиметрии. — М.: МЦНМО, 2001. — 584 с. — ISBN 5-900916-82-0 |
|||
* А. Кушниренко Целые точки в многоугольниках и многогранниках // Квант. — 1977. — № 4. — С. 13—20. |
|||
[[Категорія:Дискретна геометрія]] |
[[Категорія:Дискретна геометрія]] |
||
Версія за 21:50, 26 травня 2020

Див. також теорему в комплексному аналізі див. Лемма Шварца, теорема Шварца—Піка[en].
Якщо розглянути простий багатокутник, побудований на сітці рівновіддалених точок (тобто точок з цілі[en] координатами), так, що всі вершини багатокутника є точками сітки, теорема Піка дає просту формулу для обчислення площі S цього многокутника, за кількістю i (точок решітки усередині фігури) і кількістю b (точок решітки), розміщених по периметру многокутника:[1]
У наведеному прикладі маємо i = 7 (внутрішніх точок) і b = 8 (граничних точок), так що площа A = 7 + 82 − 1 = 7 + 4 − 1 = 10 квадратних одиниць.
Вищенаведена теорема справедлива лише для простих багатокутників, тобто для тих, які складаються з єдиної непересічної межі, без дірок. Для загального многокутника формула Піка має такий вигляд:[2][3]
де - кількість вершин всередині і на межі многокутника, - кількість точок решітки на межі многокутника, і - кількість дірок у многокутнику.
Як приклад розглянемо багатокутник, побудованний за допомогою точок . Він має 3 вершини, 0 отворів і 0 область. Щоб формула працювала, повинно бути 4 ребра. Таким чином, треба просто порахувати кожен край двічі, один раз на кожній стороні.
Результат вперше описав Георг Александр Пік в 1899.[4] Тетраедр Ріва демонструє, що немає аналоги теореми Піка в розмірності три, яка виражає об'єм багатогранника через кількість внутрішніх і граничних точок. Однак є узагальнення для високих розмірностей через многочлени Ерхарта[en].
Доведення
Розглянемо багатокутник P і трикутник T, що має з P одне спільне ребро. Припустимо, що теорема Піка справедлива як для P, так і для T незалежно один від одного; ми хочемо показати, що це також справедливо для багатокутника PT, отриманого шляхом додавання T до P. Оскільки P і T маю одне спільне ребро, всі граничні точки уздовж цього ребра стають внутрішніми точками, за винятком двох кінцевих точок, які об'єднуються з граничними точками. Отже, якщо кількість спільних граничних точок, то маємо[5]
і
З вищезазначеного випливає
і
Оскільки ми припускаємо виконання теореми і для P і для T, то
Тому, якщо теорема справедлива для многокутників побудованих з n трикутників, вона справедлива і для многокутників, що побудовані з n + 1трикутника. Добре відомо, що довільний многокутник можна розбити на симплекси триангуляція. Це тривіальний факт у випадку площини. Для завершення доведення методом математична індукція[en] достатньо довести її у випадку трикутників. Перевірку цього випадку здійснюється за допомогою наступних коротких кроків:
- припускаємо, що формула справедлива для будь-якого одиничний квадрат[en] (з вершинами, що мають цілі координати);
- на основі цього виводимо, що формула є справедливою для будь-якого прямокутник[en] зі сторонами парелельними осям;
- отримуємо формулу для прямокутних трикутників, отриманих шляхом розрізання таких прямокутників по діагональ;
- тепер будь-який трикутник можна перетворити на прямокутник, приєднавши такі прямокутні трикутники; оскільки формула виконується для прямокутних трикутників і для прямокутника, вона також буде виконуватися для початкового трикутника.
На останньому кроці застосовується той факт, що якщо теорема справедлива для багатокутника PT і для трикутника T, то це також має місце для багатокутника P; це можна побачити на основі обчислень, які подібні до наведених вище.
Нерівність для опуклих множин
Нехай — обмежена, опукла область в , не обов'язково замкнена. Тоді
.[2]
де — це набір точок решітки в , і — їх кількість. Рівність має місце тоді і лише тоді, коли — замкнений багатокутник решітки. Для доведення розглянемо опуклий оболонку для , яку слід розуміти як наближення решітки для області , а потім застосуємо до неї теорему Піка:
де — кількість граничних точок , що дорівнює кількості його ребер, і оскільки кожне ребро має мінімальну довжину 1, то
Перехід використовує властивість, що між двома вкладеними, опуклими, замкнутими кривими, внутрішня крива буде коротшою на основі прямого застосування формули Крофтона[en].
Формула залишається справедливою і у виродженому випадку, коли знаходиться на одній лінії. Потрібно просто порахувати кожен ребро двічі (по одному разу з кожної сторони).
Див. також
Список літератури
- ↑ Trainin, J. (November 2007). An elementary proof of Pick's theorem. Mathematical Gazette[en]. 91 (522): 536—540. doi:10.1017/S0025557200182270.
- ↑ а б Garbett, Jennifer (18 листопада 2010). Lattice Point Geometry: Pick's Theorem and Minkowski's Theorem, Senior Exercise in Mathematics (PDF). Архів оригіналу (PDF) за 29 Aug 2017.
- ↑ Belyaev, Alexander; Fayolle, Pierre-Alain (8 серпня 2019). Counting Parallel Segments: New Variants of Pick's Area Theorem. The Mathematical Intelligencer (англ.). 41 (4): 1—7. doi:10.1007/s00283-019-09921-8. ISSN 0343-6993.
- ↑ Pick, Georg (1899). Geometrisches zur Zahlenlehre. Sitzungsberichte des deutschen naturwissenschaftlich-medicinischen Vereines für Böhmen "Lotos" in Prag. (Neue Folge). 19: 311—319. JFM 33.0216.01. CiteBank:47270
- ↑ Beck, Matthias; Robins, Sinai (2007). Computing the Continuous Discretely: Integer-point enumeration in polyhedra. Undergraduate Texts in Mathematics. New York: Springer-Verlag. ISBN 978-0-387-29139-0.




















