Дугова діаграма: відмінності між версіями

Матеріал з Вікіпедії — вільної енциклопедії.
Перейти до навігації Перейти до пошуку
Наступне редагування →
Вилучено вміст Додано вміст
ВізуальнийВікірозмітка
Створено шляхом перекладу сторінки «Дуговая диаграмма»
(Немає відмінностей)

Версія за 09:11, 25 квітня 2022

Дугова діаграма графа Голднера — Харарі● . Червоний пунктирний відрізок показує, де можна розбити граф, щоб зробити його гамільтоновим.

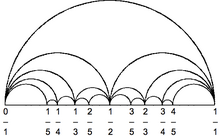
Дугова діаграма — це спосіб подання графа, в якому вершини розташовуються вздовж прямої на евклідовій площині, а ребра малюються у вигляді півкіл на одній з двох півплощин, або у вигляді гладких кривих, утворених півколами. У деяких випадках, якщо ребра з'єднують сусідні вершини на прямій, їх зображають відрізками прямої.

Назва «дугова діаграма» для такого подання графів походить від використання подібного типу діаграм Ваттенберга[1], які він використовував для візуалізації повторюваних фрагментів рядків, з'єднуючи пари однакових підрядків. Проте, сам стиль подання графа значно старший за назву і датується роботами Сааті[2] і Нікольсона[3], які використовували дугові діаграми для вивчення числа перетинів графів. Старіша, але рідше використовувана назва дугових діаграм — лінійне вкладення[4].

Хір, Босток і Огіветскі[5] написали, що дугові діаграми «не можуть виражати повної структури графа так само ефективно, як це робить двовимірне подання», але дає змогу простіше уявити багатовимірні дані, пов'язані з вершинами графів.

Планарні графи

Діаграма Фарея

Як зауважив Ніколсон[3], будь-яке вкладення графа в площину можна перетворити на дугову діаграму, не змінивши числа перетинів. Зокрема, будь-який планарний граф має планарну дугову діаграму. Однак таке вкладення може вимагати використання більш ніж одного півкола для малювання деяких ребер графа.

Якщо граф намальовано без перетинів дуг у вигляді дугової діаграми, в якій кожне ребро подано одним півколом, малюнок є двосторінковим книжковим вкладенням, що можливо тільки для підгамільтонових графів, підмножини планарних графів[6]. Наприклад, максимальний планарний граф● має таке вкладення тоді й лише тоді, коли він містить гамільтонів цикл. Таким чином, негамільтонів максимальний планарний граф, такий як граф Голднера — Харарі, не може мати планарного вкладення з одним півколом на ребро. Перевірка, чи граф має дугову діаграму без перетинів цього типу (або, еквівалентно, книжкова товщина графа дорівнює двом), є NP-повною задачею[7].

Однак будь-який планарний граф має дугову діаграму, в якій кожне ребро подано у вигляді бідуги, що складається не більше ніж з двох півкіл. Строгіше, будь-який st-планарний орієнтований граф (планарний спрямований ациклічний граф з одним витоком і одним стоком, обидва на зовнішній грані) має дугову діаграму, в якій будь-яке ребро утворює монотонну криву, всі криві (ребра) направлені в один бік[8] . Для неорієнтованих планарних графів одним зі способів побудови дугової діаграми максимум з двома півколами на ребро є поділ графа та додання додаткових ребер з метою отримати гамільтонів цикл (при цьому ребра діляться максимум на дві частини), потім використовується порядок уздовж гамільтонового циклу як порядок проходження вершин на прямій[9].

Мінімізація перетинів

Оскільки перевірка, чи має даний граф дугову діаграму без перетинів з одним півколом на ребро, є NP-повною задачею, також NP-складною задачею є пошук дугової діаграми, що мінімізує число перетинів. Завдання мінімізації числа перетинів залишається NP-складною для непланарних графів, навіть якщо порядок вершин уздовж прямої вже задано[4]. Однак, у разі заданого порядку вершин, вкладення без перетинів (якщо таке існує) можна знайти за поліноміальний час, перевівши задачу в задачу 2-виконанності[en], в якій змінні подають розташування кожної дуги, а обмеження запобігають розташуванню двох ребер, що перетинаються, по один бік від прямої з вершинами[10]. Крім того, у разі фіксованого розташування вершин, вкладення з мінімізацією числа перетинів можна апроксимувати, розв'язавши задачу максимального розрізу в допоміжному графі, який подає півкола та їх потенційні перетини[11].

Кіміковський, Шоуп[12][13], Хе, Сікора та Врто[14] обговорювали евристичні алгоритми пошуку дугових діаграм із кількома перетинами.

Орієнтація за годинниковою стрілкою

Для подання орієнтованих графів загальноприйнятим є напрямок дуг за годинниковою стрілкою, так що дуги, спрямовані зліва направо, малюються над прямою, а спрямовані справа наліво — під прямою. Цю домовленість про орієнтацію за годинниковою стрілкою розробила, як частину іншого способу подання графа, Фекет, Ванг, Данг і Аріс[15], а до дугових діаграм її застосували Преторіус і ван Вейк[16].

Інше використання

Брандес[17] використовував дугові діаграми для візуалізації діаграм станів зсувового регістра●, а а Джиджев і Врто[18] — для доведення, що число перетинів будь-якого графа принаймні дорівнює квадрату його ширини розрізу.

Примітки

  1. ↑ Wattenberg, 2002.
  2. ↑ Saaty, 1964.
  3. ↑ а б Nicholson, 1968.
  4. ↑ а б Masuda, Nakajima, Kashiwabara, Fujisawa, 1990.
  5. ↑ Heer, Bostock, Ogievetsky, 2010.
  6. ↑ Півкола для малювання ребер у книжковому вкладенні застосували вже Бернхарт і Кайнен 1979 року (Bernhart, Kainen, 1979), але явний зв'язок дугових діаграм із двосторінковими вкладеннями, очевидно, належить Масуді, Накаджимі, Кашивабарі і Фуджисаві (Masuda, Nakajima, Kashiwabara, Fujisawa, 1990).
  7. ↑ Chung, Leighton, Rosenberg, 1987.
  8. ↑ Giordano, Liotta, Mchedlidze, Symvonis, 2007.
  9. ↑ Bekos, Kaufmann, Kobourov, Symvonis, 2013.
  10. ↑ Efrat, Erten, Kobourov, 2007.
  11. ↑ Cimikowski, Mumey, 2007.
  12. ↑ Cimikowski, Shope, 1996.
  13. ↑ Cimikowski, 2002.
  14. ↑ He, Sýkora, Vrt'o, 2005.
  15. ↑ Fekete, Wang, Dang, Aris, 2003.
  16. ↑ Pretorius, van Wijk, 2007.
  17. ↑ Brandes, 1999.
  18. ↑ Djidjev, Vrt'o, 2002.

Література

Отримано з https://uk.wikipedia.org/w/index.php?title=Дугова_діаграма&oldid=35451585