Граф (математика)
| Граф | |
 | |
| Досліджується в | теорія графів |
|---|---|
| Формула | |
| Позначення у формулі | , , і |
| Підтримується Вікіпроєктом | Вікіпедія:Проєкт:Математика |
| | |
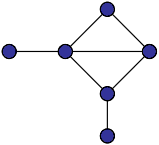
Граф — це сукупність об'єктів із зв'язками між ними.
Об'єкти розглядаються як вершини, або вузли графу, а зв'язки — як дуги, або ребра. Для різних галузей види графів можуть відрізнятися орієнтованістю, обмеженнями на кількість зв'язків і додатковими даними про вершини або ребра.
Ребра графу можуть бути напрямленими або ненапрямленими. Наприклад, якщо вершини будуть представляти людей на вечірці, й існуватиме ребро між двома людьми, якщо вони потиснули руки, тоді ребра цього графу не матимуть напряму, оскільки будь-яка особа A може потиснути руки із особою B лише якщо B також потисне руки із A. На противагу цьому, якщо будь-яке ребро від особи A до особи B означатиме, що особі A подобається B, то ребра матимуть напрям, оскільки таке вподобання не обов'язково буде взаємним. Граф першого типу називається неорієнтованим графом, а ребра в свою чергу — неорієнтованими ребрами, тоді як граф другого типу називається орієнтованим графом і ребра — орієнтованими ребрами або дугами.
Велика кількість структур, які мають практичну цінність у математиці та інформатиці, можуть бути подані графами. Наприклад, будову Вікіпедії можна змоделювати за допомогою орієнтованого графу, в якому вершини — це статті, а дуги (орієнтовані ребра) — посилання на інші статті.
Граф є основним предметом вивчення в теорії графів. Слово «граф» вперше використав в цьому сенсі Джеймс Джозеф Сильвестр 1878 року.[1][2]
Історія[ред. | ред. код]
Першою працею з теорії графів як математичної дисципліни вважають статтю Леонарда Ейлера (1736), у якій розглядалася задача про кенігсберзькі мости. Наступний імпульс теорія графів отримала близько 100 років потому з розвитком досліджень електричних мереж, кристалографії, органічної хімії та інших наук[3].
Визначення[ред. | ред. код]
Теорія графів не має стійкої термінології. В різних статтях під одними й тими ж термінами розуміють різні поняття. Наведені нижче визначення належать до найбільш розповсюджених.
Граф[ред. | ред. код]
Граф або неорієнтований граф — це впорядкована пара , для якої виконуються такі умови:
- — множина вершин або вузлів,
- — множина пар (у випадку неорієнтованого графу — невпорядкованих) вершин з , які називаються ребрами.
(і так само ) зазвичай вважають скінченними множинами. Багато результатів, отриманих для скінченних графів, неправильні (або інші) для нескінченних графів. Це пов'язано з тим, що певний набір ідей стає хибним у випадку нескінченних множин.
Граф (геометричний граф) — це фігура на площині, яка складається з непорожньої скінченної множини V точок (вершин) і скінченної множини E орієнтованих чи не орієнтованих ліній (ребер), що з'єднують деякі пари вершин.
Вершини та називаються суміжними, якщо вони з'єднані ребром . В такому разі кажуть, що вершини та інцидентні ребру , також ребро інцидентне вершинам та .
Ребра та називаються суміжними, якщо вони інцидентні вершині .
Орієнтований граф[ред. | ред. код]
Граф, який містить тільки ребра називається неорієнтованим, який містить тільки дуги — орієнтованим. Граф, що має як ребра так і дуги, називається мішаним.
Іноді є потреба пару вершин з'єднати більше, ніж одним ребром. Ребра чи дуги одного напряму, які з'єднують ту саму пару вершин, називаються кратними (паралельними) ребрами.
Дуга чи ребро, що сполучає вершину саму зі собою називається петлею.
Граф без кратних дуг і петель називається простим.
Вершини сполучені ребром чи дугою називаються суміжними, також називаються суміжними ребра, що мають спільну вершину. Ребро (чи дуга) і її вершина називаються інцидентними. Ребро (u, v) з'єднує вершини u і v, дуга (u, v) починається у вершині u і закінчується у вершині v.
Кожен граф можна відобразити в евклідовому просторі множиною точок, які відповідають вершинам, сполучених лініями, що відповідають ребрам (дугам).
Мультиграфом називається пара , де — множина, елементи якої називаються вершинами. — сім'я ребер, кожне з яких — це пара вершин із .
Мультиграф, який може мати петлі, іноді називають псевдографом.
| Тип графу | Ребра | Кратні ребра |
|---|---|---|
| Простий граф | Неорієнтовані | Ні |
| Мультиграф | Неорієнтовані | Так |
| Орієнтований граф | Орієнтовані | Ні |
| Орієнтований мультиграф | Орієнтовані | Так |
Поняття[ред. | ред. код]
- Цикл — замкнутий ланцюг, для орієнтованих графів цикл називається контуром.
- Цикл в орієнтованому графі — це простий шлях довжини не менше 1, котрий починається і закінчується в одній і тій самій вершині.
- Дерево — зв'язний граф без циклів.
Способи подання графу в пам'яті комп'ютера[ред. | ред. код]
Якщо мережу автомобільних доріг, ліній комунікацій чи будь-який граф взагалі треба використати в комп'ютерній програмі, то постає проблема збереження інформації про цей граф у пам'яті комп'ютера. Вибір структури даних для збереження графу в пам'яті є визначальним у процесі розробки ефективних алгоритмів.
Надалі вважатимемо, що вершини графу мають номери від 1 до N, а ребра — від 1 до M. Кожному ребру і кожній вершині зіставлена вага — ціле додатне число.
Матриця суміжності[ред. | ред. код]
Матриця суміжності це двовимірний масив розміром N*N:
// матриця суміжності
Type TAdjacencyMatrix = array [1..N, 1..N] of Integer;
Var Graph: TAdjacencyMatrix;
При цьому Graph[i, j] дорівнює 0, якщо вершини i та j не є суміжними, та 1 для суміжних вершин. Для зваженого графу Graph[i, j] дорівнює вазі вершини i, якщо i=j, а для суміжних вершин — вазі ребра (дуги) з вершини i у вершину j.
Просторова складність цього способу O(N2)
Цей спосіб застосовують тоді, коли в задачі треба часто перевіряти суміжність чи знаходити вагу ребра за двома заданими вершинами.
Матриця інцидентності[ред. | ред. код]
- Детальніше Матриця інцидентності
Матриця інцидентності це двовимірний масив розміром N*M:
// матриця інцидентності
Type TIncidenceMatrix = array [1..N, 1..M] of Integer;
Var Graph: TIncidenceMatrix;
При цьому Graph[i, j] дорівнює 0, якщо вершини i та ребро j не є інцидентними, −1, якщо вершина i є кінцем орієнтованого ребра j, +1, якщо вершина i є початком орієнтованого ребра j. Інколи зручно користуватись означенням, у якому Graph[i, j] дорівнює вазі ребра (дуги) j, що є інцидентним вершині i.
Матриця інцидентності найкраще підходить для операції перерахування ребер, що є інцидентними вершині x.
Списки суміжності[ред. | ред. код]
- Детальніше Список суміжності
Список суміжності це послідовність (масив, список) розміром N, кожен елемент якої є списком вершин суміжних з даною:
// список суміжності
Type TAdjacencyList = array [1..N] of record
Count: Integer; {кількість елементів у списку}
List: array[1..N] of
record {список}
Node, {номер суміжної вершини}
Weight: Integer; {вага ребра}
end;
end;
Var Graph: AdjacencyList;
Цей спосіб збереження найкраще підходить для перерахування усіх вершин суміжних з x.
Список ребер[ред. | ред. код]
- Детальніше Список ребер
// динамічний список ребер (із вказівниками)
// застосовують тоді, коли кількість ребер невідома наперед і їх багато
Type ListElPtr=^ListEl; {вершини графа позначені числами }
{(номерами)}
ListE l= record
Node1, Node2: integer; {список складаються із пар цілих чисел: }
{перше - звідки ребро, друге - куди}
Next:ListElPtr; {вказівник на наступне ребро графа}
end;
// список (масив) ребер
// застосовують тоді, коли кількість ребер відома наперед і невелика
Type TBranchList = array [1..M] of
record
Node1, Node2, {пари вершин, що зв'язує ребро}
Weight: Integer; {вага ребра}
end;
Var Graph: BranchList;
Цей спосіб збереження графу є особливо зручним, якщо головною операцією є перерахування ребер або пошук вершин і ребер, що знаходяться у відносинах інцидентності.
Застосування графів[ред. | ред. код]
Графи використовуються в різних галузях науки і техніки, зокрема:
- Файлова система комп'ютера. Ієрархія файлів та тек в багатьох операційних системах має вигляд дерева, яке є окремим випадком графу;
- Молекули всіх хімічних речовин можна зобразити у вигляді графу, де атоми є вершинами, а зв'язки між ними — ребрами;
- Карта автомобільних чи будь-яких інших шляхів також є графом, причому кожна дорога може мати певне значення «ваги» (наприклад, щільність транспортного потоку), тоді такий граф є зваженим;
- Соціальну мережу також можна подати у вигляді графу, де кожна людина чи соціальна група є вершиною, а зв'язки між ними — ребрами;
- Генеалогічне дерево є прикладом бінарного дерева, яке є окремим випадком графу;
- Турнірну таблицю спортивного чемпіонату також можна зобразити у вигляді графу;
- В біології та екології також використовуються графи. Прикладами є ланцюги харчування, екосистеми, генетичні послідовності та карти, таксономічна ієрархія живих організмів тощо;
- В археології та геології графи використовуються у стратиграфії для вивчення геологічних пластів;
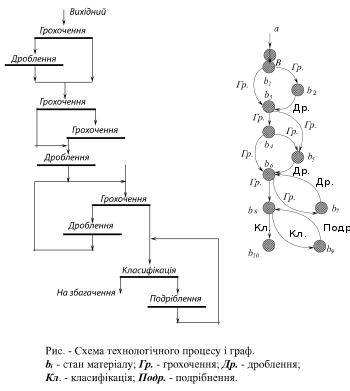
- Будь-який виробничий процес також можна зобразити у вигляді графу (див. приклад — технологічна схема збагачення корисних копалин);
- Розробка програмного забезпечення та комп'ютерні науки взагалі є однією з тих галузей, де графи застосовуються найчастіше. Складність та велика кількість модулів і протоколів у сучасних програмних продуктах дуже ускладнює розуміння їх роботи, керування нею та її оптимізацію, тому дуже часто складаються графи програм, причому найчастіше це робиться автоматично трансляторами чи компіляторами. Графи також є зручними для зображення структур даних, блок-схем, потоків даних, схем баз даних та баз знань, скінченних автоматів, схем комп'ютерних мереж та окремих сайтів, схем викликів підпрограм тощо. Також графи широко використовуються в багатьох алгоритмах пошуку та сортування. Крім того, одним з головних напрямків сучасних досліджень у царині глобальних мереж є задане консорціумом W3C завдання побудови семантичної мережі (один з видів графів) на базі мережі Інтернет.
Див. також[ред. | ред. код]
- Операції над графами
- Дерево (теорія графів)
- Цикломатичне число
- Маршрут (теорія графів)
- Матриця суміжності
- Словник термінів теорії графів
- Граф хімічних реакцій
- Хімічна теорія графів
- Мережа
- Центр графа
- Циклічний ранг
- Ранг (теорія графів)
Література[ред. | ред. код]
- Спекторський І. Я. Дискретна математика. — К. : Політехніка. — 220 с. — ISBN 966-622-136-5.
- J.A. Bondy, U.S.R. Murty (1976). Graph Theory with Applications. Elsevier/North-Holland. с. 264 c. ISBN 0-444-19451-7. Процитовано 27 квітня 2008.
{{cite book}}: Обслуговування CS1: Сторінки з параметром url-status, але без параметра archive-url (посилання) (англ.) - J.A. Bondy, U.S.R. Murty (2008). Graph Theory. Springer. с. 654 c. ISBN 978-1-84628-969-9. Архів оригіналу за 11 травня 2008. Процитовано 27 квітня 2008. (англ.)
- Jungnickel, Dieter (2008). Graphs, Networks and Algorithms. Springer. с. 650 c. ISBN 978-3-540-72779-8. Архів оригіналу за 13 червня 2008. Процитовано 30 квітня 2008. (англ.)
- Сик Дж., Ли Л., Ламсдэйн Э. (2006). C++ Boost Graph Library. Питер. с. 304 c. ISBN 978-5-469-00352-6. (англ.)
- Robert Sedgewick (2003). Algorithms in Java, Third Edition, Part 5: Graph Algorithms. Addison Wesley. с. 528 c. ISBN 0-201-36121-3. (англ.)
- Березина Л. Ю. Графы и их применение. — М. : URSS, 2009. — 152 с.(рос.)
- Берж К. Теория графов и ее применения. — М. : ИЛ, 1962. — 320 с.(рос.)
- Голиков А. П., Черванёв И. Г., Трофимов А. М. Математические методы в географии. — Х. : Изд-во ХГУ, 1986. — 143 с.(рос.)
- Ловас Л., Пламмер М. Прикладные задачи теории графов. — М. : Мир, 1998. — 656 с.(рос.)
- Михеева В. С. Приложение теории графов: Курс лекций (ч. 2) // Математические методы в экономической географии. — М. : Изд-во МГУ, 1983.(рос.)
- Оре О. Теория графов. — М. : Наука, 1980. — 336 с.(рос.)
- Татт У. Теория графов. — М. : Мир, 1988. — 424 с.(рос.)
- Фляйшнер Г. Эйлеровы графы и смежные вопросы. — М. : Мир, 2002. — 176 с.(рос.)
- Харари Ф. Теория графов. — М. : Мир, 1973. — 304 с.(рос.)
Примітки[ред. | ред. код]
- ↑ Див.:
- J. J. Sylvester (February 7, 1878) "Chemistry and algebra, " [Архівовано 5 червня 2020 у Wayback Machine.] Nature, 17 : 284. DOI:10.1038/017284a0. From page 284: «Every invariant and covariant thus becomes expressible by a graph precisely identical with a Kekuléan diagram or chemicograph.»
- J. J. Sylvester (1878) "On an application of the new atomic theory to the graphical representation of the invariants and covariants of binary quantics, — with three appendices, " [Архівовано 5 червня 2020 у Wayback Machine.] American Journal of Mathematics, Pure and Applied, 1 (1) : 64–90. DOI:10.2307/2369436. JSTOR 2369436. The term «graph» first appears in this paper on page 65.
- ↑ Gross, Jonathan L.; Yellen, Jay (2004). Handbook of graph theory. CRC Press. с. 35. ISBN 978-1-58488-090-5.
- ↑ (рос.) Белоусов А. И., Ткачев С. Б. Дискретная математика: Учебник для вузов / Под ред. В. С. Зарубина, А. П. Крищенко. — 3-е изд., стереотипное. — М.: Издательство МГТУ им. Н. Э. Баумана, 2004. ISBN 5-7038-1270-4.
| Це незавершена стаття з математики. Ви можете допомогти проєкту, виправивши або дописавши її. |
| Ця стаття містить перелік посилань, але походження тверджень у ній залишається незрозумілим через практично повну відсутність внутрішньотекстових джерел-виносок. (серпень 2020) |













