Metaball

2. Взаємодія позитивної та негативної метасфери створює вм'ятину на позитивній метасфері.
Metaball (укр. метасфера, також зустрічається «метаболл») — n-мірний об'єкт в комп'ютерній графіці, що являє собою замкнуту згладжену поверхню. Техніка рендерингу метасфер була винайдена Джимом Блінном (англ. Jimm Blinn) на початку 1980-х років.
Використання полігонів в комп'ютерній графіці часто дає не згладжені моделі, причому ступінь згладження сильно залежить від масштабу. Для отримання гладких поверхонь використовуються різні методи, такі як B-сплайни і поверхні Безьє. При використанні метасфер мається на увазі, що в просторі задано безліч керуючих точок, що володіють потенціалом, і задані функції залежності потенціалу від відстані, таким чином обчислюючи потенціал поля, можна побудувати згладжені ізоповерхні досить складної форми.
Кожна керуюча точка визначає власну n-мірну потенційну функцію (зазвичай n = 3). Потім вибирається якесь значення (потенціал), яке визначає форму метасфери (фактично, визначається Еквіпотенціальна поверхня). Таким чином, нерівність визначає, чи знаходиться точка (x, y, z) всередині поверхні, заданої керуючими точками, чи ні.
Часто як функцію, яка задає метасферу, використовують , де — центр метасфери. Проте використання ділення робить цю функцію неефективною за швидкістю, тому зазвичай її замінюють апроксимуючими поліноміальними функціями.
При пошуку більш ефективної функції потенціалу бажано, щоб вона задовольняла таким вимогам:
- Компактність носія. Така функція перетворюється в нуль за межами якоїсь обмеженої сфери. При обчисленні поля, створюваного керуючою точкою, немає необхідності обчислювати його, коли відстань перевищує радіус обмеженої сфери. Ієрархічна система відсікань може, таким чином, сильно скоротити кількість керуючих точок, необхідних для розрахунку поля в даній точці.
- Гладкість. Оскільки метасфер є результатом суперпозиції полів керуючих точок, її гладкість залежить від гладкості функції потенціалу.
Найпростіша функція потенціалу, задовольняє цим критеріям: , де — відстань між керуючою точкою і заданою точкою простору. Вона також досить ефективна, оскільки не використовує ділення і обчислення кореня.
Більш складні моделі використовують для кращого згладжування потенціал Гауса, обмежений кінцевим радіусом набору многочленів. Модель м'яких об'єктів братів Вівілл (англ. Wyvill) забезпечує більш високий ступінь згладженості та не використовує квадратні корені.
Просте узагальнення моделі можна отримати, замінюючи відстань між точками у функції потенціалу відстанню до прямої або відстанню до поверхні.
Є безліч способів рендеринга метасфер. Для тривимірних метасфер найчастіше застосовують рейкастинг і алгоритм marching cubes.
Двомірні метасфери були дуже популярні в демосценах у 1990-х. Цей ефект також доступний у модулі XScreensaver.
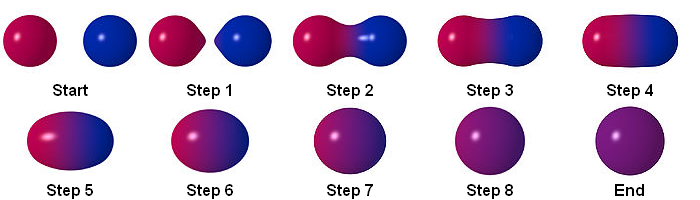
Зверніть увагу, як дві маленьких метасфери зливаються в одну велику.
- Blinn, James F. «A Generalization of Algebraic Surface Drawing.» ACM Transactions on Graphics 1(3), July 1982, pp. 235–256.
- Неявні поверхні — стаття Поля Бурке (англ.)
- Метаоб'єкти на Blender- вікі (англ.)
- Метасфери на сайті SIGGRAPH (англ.)
- Дослідження метасфер та ізоповерхонь на площині (стаття на GameDev.net)
- Використання двовимірних сфер в Photoshop (англ.)
- Вступ у метасфери [Архівовано 13 квітня 2015 у Wayback Machine.] (англ.)







