Великий ікосаедр

Великий ікосаедр
Тип	Тіло Кеплера — Пуансо, дельтаедр
Зірчаста форма	Правильного ікосаедра
Властивості	Неопуклий, рівносторонній, правильний зірчастий багатогранник, гране-транзитивний, вершинно-транзитивний.
Комбінаторика
Елементи	20 граней; 30 ребер; 12 вершин 5-го степеня.
Грані {p}	20 Правильних трикутників = 20{3}.
Характеристика Ейлера	$\chi =\Gamma -{\hbox{P}}+{\hbox{B}}=2$
Конфігурація вершини	(3.3.3.3.3)/2 = (35) / 2 (тобто кожна вершина оточена п'ятьма трикутниками, що перетинаються)
Конфігурація грані	V(53) / 2
Вершинна фігура	Пентаграма {5/2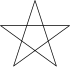} :ст.436; , з довжиною сторони $1$
Щільність	7
Рід	0
Класифікація
Позначення	• W41 (в нотації М. Веннінґера) • U53 (як однорідний багатогранник) • C69 (в нотації Г.Коксетера) :ст.436
Символ Шлефлі {p, q}	{3, 5/2}
Діаграма Коксетера — Динкіна	(або x3o5/2o)
Символ Витгоффа	5/2 | 2 3
Група симетрії	Ih, H3, [5,3], (*532), порядок 120 (Повна симетрія правильного ікосаедра)
Двоїстий багатогранник	Великий зірчастий додекаедр

Великий ікосаедр ^{:стор.40-41 ; :стор.443-444} — один з чотирьох правильних зірчастих багатогранників Кеплера — Пуансо.

Цей багатогранник було відкрито у 1809 році Луї Пуансо ; ^{:стор.149}, а назву йому дав Артур Кейлі в 1859 році. ^{:стор.410}

Він складається з 20 граней — правильних трикутників (десять пар трикутних граней лежать в паралельних площинах), по 5 трикутників у кожній вершині, що перетинаються між собою. Має 12 вершин, кожна з яких є вершиною зірчастого п'ятигранного кута.

Його символ Шлефлі — $\left\{3,{\frac {5}{2}}\right\}$. Це означає, що кожна вершина оточена п'ятьма правильними трикутниками, що перетинаються між собою; або також це означає для багатогранника, що його грань — правильний трикутник, а вершинна фігура — правильна п'ятипроменева зірка (пентаграма). ^{:стор.410}

Оскільки всі грані великого ікосаедра правильні трикутники, то цей багатогранник є дельтаедром.

Має центральну ділянку кожної грані у вигляді зірчастого багатокутника, «приховану» всередині багатогранника, при цьому зовні видно тільки ділянки граней у вигляді різносторонніх та рівнобедрених трикутників (певного розміру).

Розташування вершин великого ікосаедра таке ж як і у правильного ікосаедра (тобто опукла оболонка великого ікосаедра є правильним ікосаедром). Також розташування вершин та розташування ребер великого ікосаедра повністю збігається з розташуваннями вершин та ребер малого зірчастого додекаедра.

Великий ікосаедр має повну симетрію правильного ікосаедра, і отже, всі його елементи симетрії, а саме:

1) має 31 вісь обертової симетрії:

‒ 6 осей 5-го порядку — проходять через протилежні вершини;

‒ 10 осей 3-го порядку — проходять через протилежні точки, в яких перетинаються по три грані;

‒ 15 осей 2-го порядку — проходять через середини протилежних паралельних ребер.

2) має 15 площин дзеркальної симетрії, що проходять через кожні дві сусідні вершини та центр багатогранника (через кожну пару паралельних ребер).

3) має центр симетрії.

Як зірчаста форма правильного ікосаедра

Діаграма ззірчення правильного ікосаедра та грань великого ікосаедра на ній	Жовтим кольором зображено грань великого ікосаедра	Утворення грані великого ікосаедра

Правильний ікосаедр має 59 зірчастих форм, з яких 32 мають повну, а 27 — неповну ікосаедричну симетрію, що довів Гарольд Коксетер спільно з дю Валем, Флезером (H.T. Flather) і Петрі (John Flinders Petrie) із застосуванням правил обмеження, встановлених Дж. Міллером.

Великий ікосаедр є однією з зірчастих форм правильного ікосаедра, яка в різних класифікаціях має різний порядковий номер. За версією М.Веннінґера, він є 16-ю зірчастою формою ікосаедра. В третьому виданні книги Г.Коксетера «59 ікосаедрів» Кейт та Девід Креннели (Crennell) повністю переробили початкову класифікацію Коксетера, і в ній великий ікосаедр описано під номером 7.

Позначення великого ікосаедра як зірчастої форми в нотації дю Валля — G.

З усіх зірчастих форм ікосаедра, великий ікосаедр є єдиним правильним багатогранником.

Великий ікосаедр утворюється з правильного ікосаедра при продовженні (розширенні) його граней. Кожна грань правильного ікосаедра розширюється до її взаємного перетину з трьома гранями, що суміжні з паралельною до неї гранню..^{:стор.443-444}

Якщо кожну з граней ікосаедра продовжити необмежено, то взаємно перетинаючись, вони розмежують простір на 20 + 30 + 60 + 20 + 60 + 120 + 12 + 30 + 60 + 60 = 472 відсіки (комірки). Усі повнотілі зірчасті форми ікосаедра (ті, що не містять розривів та пустот) можна отримати послідовним приєднанням до початкового тіла таких комірок (хоча строго кажучи зірчастий багатогранник утворюється від перетину несуміжних граней деякого опуклого багатогранника, а не приєднанням частин до нього). Великий ікосаедр складається з усіх цих комірок, за винятком останніх шестидесяти, та є 11-ю зіркою (рахуючи від ікосаедра). Wills Stellation of the Icosahedron (3) на YouTube

Діаграма ззірчення правильного ікосаедра з пронумерованими наборами граней ^{:стор.19, фіг.4}

Його грані складені з 0 по 12-ту секції на діаграмі ззірчення правильного ікосаедра. Зовні видно 11-ту та 12-ту секції.

Частина граней, що знаходиться всередині багатогранника відіграє роль плоскої мембрани та не розмежовує внутрішній простір багатогранника.

Формули

Грань великого ікосаедра та її елементи.

У всіх формулах нижче: $\varphi ={\frac {1+{\sqrt {5}}}{2}}\approx 1.6180339887$ — відношення пропорції «золотого перетину». (послідовність A001622 з Онлайн енциклопедії послідовностей цілих чисел, OEIS).

Рівносторонній трикутник △ KLM — грань базового правильного ікосаедра, з якого утворена грань великого ікосаедра (△ ABC).

В великий ікосаедр можна вписати правильний додекаедр так, що всі ребра останнього будуть лежати на ребрах великого ікосаедра (На рисунку грані його сторона відповідає відрізку DE ).

Розміри деяких елементів на грані великого ікосаедра

	Якщо ребро вписаного додекаедра = 1			Якщо ребро великого ікосаедра = 1			Якщо ребро базового ікосаедра =1
$AB=$	${\sqrt {5}}+2=2\varphi +1=\varphi ^{3}$	$\approx 4.23607$		$1$			${\frac {7+3{\sqrt {5}}}{2}}=3\varphi +2=\varphi ^{4}$	$\approx 6.854102$
$AD=BE=$	${\frac {{\sqrt {5}}+1}{2}}=\varphi$	$\approx 1.61803$		${\frac {3-{\sqrt {5}}}{2}}=2-\varphi ={\frac {1}{\varphi ^{2}}}$	$\approx 0.38197$		${\frac {3+{\sqrt {5}}}{2}}=\varphi +1=\varphi ^{2}$	$\approx 2.61803$
$DE=$	$1$			${\sqrt {5}}-2=2\varphi -3={\frac {1}{\varphi ^{3}}}$	$\approx 0.23607$		${\frac {{\sqrt {5}}+1}{2}}=\varphi$	$\approx 1.61803$
$AF=BH=$	${\sqrt {\frac {7+3{\sqrt {5}}}{5}}}$	$\approx 1.65579$		${\sqrt {\frac {3-{\sqrt {5}}}{5}}}$	$\approx 0.39088$		${\sqrt {{\frac {2}{5}}(9+4{\sqrt {5}})}}$	$\approx 2.67912$
$DF=EH=$	${\frac {\sqrt {10}}{5}}$	$\approx 0.63246$		${\sqrt {{\frac {2}{5}}(9-4{\sqrt {5}})}}={\frac {\sqrt {10}}{5\cdot \varphi ^{3}}}$	$\approx 0.149302$		${\frac {\sqrt {2}}{10}}(5+{\sqrt {5}})={\frac {\sqrt {10}}{5}}\cdot \varphi$	$\approx 1.02333$
$DG=EG=$
$KL=$	${\frac {{\sqrt {5}}-1}{2}}={\frac {1}{\varphi }}$	$\approx 0.61803$		${\frac {7-3{\sqrt {5}}}{2}}={\frac {1}{\varphi ^{4}}}$	$\approx 0.145898$		$1$
Кути грані' :стор.97
Кут $\alpha =$	$\arccos \left({\frac {\sqrt {10}}{4}}\right)$			≈ 0.659058035827 рад ≈ 37° 45′ 40.478065326′′
Кут $\beta =$	$\arccos \left(-{\frac {1}{4}}\right)$			≈ 1.823476581937 рад ≈ 104° 28′ 39.04386934′′
Кут $\gamma =$	$\arccos \left({\frac {\sqrt {2}}{8}}(3-{\sqrt {5}})\right)$			≈ 1.435337066566 рад ≈ 82° 14′ 19.521934674′′
Кут $\delta =$	$\arccos \left({\frac {1}{4}}\right)$			≈ 1.31811607165 рад ≈ 75° 31′ 20.956130652′′
Кут $\omega =$	$\arccos \left({\frac {\sqrt {7+3{\sqrt {5}}}}{4}}\right)$			≈ 1.823476581937 рад ≈ 22° 14′ 19.52193467′′

Для великого ікосаедра з довжиною ребра $a$:
Радіус описаної сфери (проходить через всі вершини)	$R={\frac {1}{2}}\cdot {\sqrt {\frac {5-{\sqrt {5}}}{2}}}\cdot a={\frac {\sqrt {3-\varphi }}{2}}\cdot a$	≈ 0.587785252$\cdot a$
Радіус напіввписаної сфери (дотикається до всіх ребер)	$\rho ={\frac {{\sqrt {5}}-1}{4}}\cdot a={\frac {\varphi -1}{2}}\cdot a$	≈ 0.309016994$\cdot a$
Радіус вписаної сфери (дотикається до всіх граней)	$r={\frac {\sqrt {3}}{12}}\cdot (3-{\sqrt {5}})\cdot a={\frac {1}{2}}\cdot {\sqrt {\frac {7-3{\sqrt {5}}}{6}}}\cdot a={\frac {\sqrt {3}}{6\cdot \varphi ^{2}}}\cdot a$	≈ 0.1102640897$\cdot a$
Площа поверхні	$S=3{\sqrt {3}}\cdot (16{\sqrt {5}}-35)\cdot a^{2}=3{\sqrt {15}}\cdot \left(23-14\varphi \right)\cdot a^{2}$	≈ 4.037865823$\cdot a^{2}$
Об'єм	$V={\frac {1}{4}}\cdot \left(83{\sqrt {5}}-185\right)\cdot a^{3}$	≈ 0.148410533$\cdot a^{3}$
Двогранний кут між гранями	$\alpha =\arccos \left({\frac {\sqrt {5}}{3}}\right)$	≈ 0.729727656 рад ≈ 41°48′ 37.13362′′ (послідовність A156547 з Онлайн енциклопедії послідовностей цілих чисел, OEIS)

Радіус вписаної сфери — рідіус сфери, вписаної в базовий ікосаедр, з якого отримана грань великого ікосаедра; довжина ребра базового ікосаедра дорівнює ${\frac {7-3{\sqrt {5}}}{2}}\cdot a={\frac {1}{\varphi ^{4}}}\cdot a\approx 0.145898\cdot a$.

Центр мас великого ікосаедра знаходиться в його геометричному центрі.

Момент інерції суцільного великого ікосаедра з одиничною масою та одиничною довжиною ребра:

$I={\frac {3-{\sqrt {5}}}{20}}\approx 0.0381966011$

Координати вершин

Як було зазначено вище, розташування вершин великого ікосаедра таке ж як і у правильного ікосаедра та малого зірчастого додекаедра. А отже, вершини великого ікосаедра в декартовій системі координат мають такі ж координати як і вершини правильного ікосаедра або малого зірчастого додекаедра або великого додекаедра (з урахуванням маштабування щодо довжини ребра).

Пов'язані та споріднені багатогранники

Розташування вершин великого ікосаедра таке ж як і у правильного ікосаедра (тобто опукла оболонка великого ікосаедра є правильним ікосаедром). Також розташування вершин та розташування ребер великого ікосаедра повністю збігається з розташуваннями вершин та ребер малого зірчастого додекаедра.

Анімація послідовності зрізання великого зірчастого додекаедра від { ⁵⁄₂, 3} до {3, ⁵⁄₂}

Існує чотири неопуклих однорідних багатогранників, що утворені певними ступенями операції зрізання великого ікосаедра.

Зрізаний великий ікосаедр є однорідним неопуклим багатогранником U₅₅, що має діаграму Коксетера — Динкіна та символ Шлефлі t{3,5/2}. Має 32 граней (12 правильних п'ятипроменевих зірок (пентаграм) та 20 правильних шестикутників), 90 ребер та 60 вершин.

Великий ікосододекадр утворюється при повному зрізанні (ректифікації) великого зірчастого додекаедра, коли зрізання вершин проводиться до точок, що лежать на серединах ребер багатогранника, тобто ребра початкового багатогранника фактично зникають.

Зрізаний великий зірчастий додекаедр можна вважати виродженим неопуклим однорідним багатогранником. Вершини великого зірчастого додекаедра зрізаються до тих пір, доки повністю не зникнуть «трикутні піраміди».

Візуально він виглядає як правильний ікосаедр, але має 32 грані — 20 правильних трикутників, утворених від зрізання вершин і 12 п'ятикутників, утворених від зрізання пентаграм, що знаходяться всередині багатогранника. П'ятикутники зі зрізаних пентаграм насправді є виродженими десятикутниками {10/2}, що приймають форму подвійно-накритих п'ятикутників із двома множинами вершин і ребер, накладених одне на одне.

Коли ⁿ⁄_d -кутник скорочується в процесі зрізання, він стає ²ⁿ⁄_d -кутником.

Наприклад, зрізаний п'ятикутник { ⁵⁄₁} стає десятикутником { ¹⁰⁄₁}, а зрізана пентаграма { ⁵⁄₂} стає подвійно-накритим п'ятикутником (тобто десятикутником, що має форму п'ятикутника) { ¹⁰⁄₂} (це означає, що ми відвідаємо кожну вершину двічі, щоб завершити багатокутник).

Багатогранник має 60 вершин (в кожній вершині «ікосаедра» містяться п'ять суміщених вершин багатогранника) та 90 ребер (кожне ребро «ікосаедра» є потрійним — одне ребро від зрізання вершини (вершинна фігура — опуклий правильний трикутник) та два ребра від зрізання пентаграми).

Найбільш наближеним до нього багатогранником є малий складений ікосододекаедр, який також має зовнішній вигляд ікосаедра та внутрішні п'ятикутні грані, але має іншу кількість вершин та ребер.

Процес зрізання великого ікосаедра завершується (при повному глибокому зрізанні або біректифікації) утворенням двоїстого до нього багатогранника — великого зірчастого додекаедра, коли грані початкового багатогранника зменшуються до точок, тобто фактично зникають.

Назва	Великий ікосаедр	Зрізаний великий ікосаедр	Великий ікосододекадр	Зрізаний великий зірчастий додекаедр	Великий зірчастий додекаедр
Діаграма Коксетера — Динкіна	x3o5/2o	x3x5/2o	o3x5/2o	o3x5/2x	o3o5/2x
Символ Шлефлі	{3,5/2}	t{3,5/2}	r{3,5/2}	t{5/2,3}	{5/2,3}
Зображення

Два однорідних з'єднання багатогранників складаються з великих ікосаедрів:

З'єднання двох великих ікосаедрів	З'єднання п'яти великих ікосаедрів

Як кирпатий багатогранник

Великий ікосаедр можна побудувати, застосувавши до трикутника Шварца (2 3 5/2) геометричну операцію однорідного «зрізання носів» (снубіфікацію) в означенні Коксетера. При цьому утвориться багатогранник візуально схожий на великий додекаедр, але з меншою тетраедричною симетрією: , всі грані якого — різнотипні.

Таку конструкцію можна назвати ретрокирпатим тетраедром або ретрокирпатим тетратетраедром . за аналогією з ікосаедром з піритоедричною симетрією, як часткової огранки зрізаного октаедра (або омнітрункованого^[en] тетраедра): .

Також можливо побудувати багатогранник, схожий на великий ікосаедр з двома типами граней та піритоедричною симетрією з діаграмами Коксетера — Динкіна або , який можна назвати ретрокирпатим октаедром.

Якщо початковий багатогранник (або паркет) має символ Шлефлі {p, q}, то ретрокирпатий багатогранник (або паркет) буде мати конфігурацію вершини (3.3.p.3.q)/2 (тобто як звичайний кирпатий багатогранник, але з чергуванням вершин).

Тетраедрична симетрія	Піритоедрична симетрія
		Великий ікосаедр з піритоедричною симетрією

Додатково

Деякі ортогональні проєкції великого ікосаедра :

Проєкція, ортогональна до осі симетрії 5-го порядку

Проєкція, ортогональна до осі симетрії 3-го порядку

Проєкція, ортогональна до осі симетрії 2-го порядку

Складання моделі багатогранника

Елемент розгортки великого ікосаедра

Великий ікосаедр можна скласти з паперу, з'єднавши разом 12 прямих пентаграмних пірамід (без основи). Кожен трикутник в цій розгортці візуально представляє частину правильного трикутника — грані великого ікосаедра.

Теоретично великий ікосаедр є жорстким багатогранником (тобто його не можна безперервно деформувати в іншу конфігурацію без згинання або розриву). Але практично, через велику кількість згинів трикутних частин граней почергово в протилежні сторони, що зустрічаються в вершинах та «хибних вершинах» (точки перетину граней, що не є вершинами багатогранника), модель не є жорсткою та легко деформується.

Тому для забезпечення жорсткости моделі її доцільно будувати трохи в інший спосіб. А саме, побудувати спершу основу — виїмчастий додекаедр^[en] (або також увігнутий пентакісдодекаедр ). Виїмчастий додекаедр^[en] є однією з зірчастих форм правильного ікосаедра (позначення в нотації дю Валля — Ef₁g₁.). Ці багатогранники візуально схожі (відрізняються кількістю вершин, ребер та формою граней) однак моделі можуть бути побудовані з правильних трикутників. Потім до цієї основи прикріпити зірчасті піраміди, виготовлені по шаблону, вказаному на рисунку, попередньо укріпивши їх зсередини правильними трикутниками. · ^{:стор.98-99}

Багатокутники Петрі

Багатокутник Петрі великого ікосаедра
Просторовими багатокутниками Петрі великого ікосаедра є 6 просторових десятипроменевих зірок (декаграм).

Інше

Обертання багатогранника	Сферична проєкція	Щільність
	Цей багатогранник також можна подати у вигляді сферичної плитки зі щільністю 7. (Одна сферична трикутна грань, обведена синім і заповнена жовтим кольорами)	Багатогранник має щільність 7, що видно на цьому перерізі.

Див. також

• Однорідний зірчастий многогранник
• З'єднання великого зірчастого додекаедра та великого ікосаедра

Література

• M. Wenninger. Polyhedron Models. — Cambridge University Press, 1974. — ISBN 0-521-09859-9.
• Magnus J. Wenninger (1975). Polyhedron Models for the Classroom. (PDF) (англ.) . № Вид. 2-ге. National Council of Teachers of Mathematics, Inc.,Reston, Va. с. 64.
• H. S. M. Coxeter. Uniform polyhedra / M. S. Longuet-Higgins, J. C. P. Miller // Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences. — The Royal Society, 1954. — Т. 246, № 916. — С. 401—450. — ISSN 0080-4614. — DOI:10.1098/rsta.1954.0003.

• Louis Poinsot. Memoire sur les polygones et polyèdres. — J. de l'École Polytechnique. — 1810. — Т. 9. — P. 16-48.

• Richeson, D.S. (2008). Euler's Gem: The Polyhedron Formula and the Birth of Topology. Princeton University Press. с. 151. ISBN 9780691126777. LCCN 2008062108.

• H. S. M. Coxeter, Patrick du Val, H.T. Flather, J.F. Petrie. The Fifty-nine Icosahedra. — University of Toronto studies, 1938. — P. 1-26. — (mathematical series 6)
  • 3-тє видання (1999), видавництва Tarquin ISBN 978-1-899618-32-3 MR676126

• Henry Martyn Cundy, A. P. Rollett. Mathematical Models. — 2-ге. — Oxford University Press / Clarendon, 1961. — P. 96-99.
• H.S.M. Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, 3.6 6.2 Stellating the Platonic solids, pp. 96–104

• H. S. M. Coxeter. Star polytopes and the Schläfli function f(α,β,γ) // Elemente der Mathematik. — 1989. — Vol. 44, iss. 2. — P. 25-36. — ISSN 0013-6018.

• Arthur Cayley. The Collected Mathematical Papers. — Richmond, Surrey : Garden House, Cambridge, 1891. — Т. 4. — С. 82-87. — (On Poinsot’s Four New Regular Solids (розділ 241-242 ))
• Cayley, Arthur (1859). XIX. On Poinsot's four new regular solids. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. Taylor & Francis. 17 (112): 123—128.

• Vilko Domajnko (2000/2001). Zvezdni poliedri (PDF). Presek (словен.) . 28 (2): 68—73.

Посилання

• Weisstein, Eric W. Великий ікосаедр(англ.) на сайті Wolfram MathWorld.
  • Weisstein, Eric W. Зірчасті форми ікосаедра(англ.) на сайті Wolfram MathWorld.

• Great icosahedron(англ.) на сайті Polytope Wiki.
• Great Icosahedron (англ.) на сайті dmccooey.com.
• Nan Ma. «Great icosahedron {3, 5/2}»
• Klitzing, Richard. «gike»
• Однорідні багатогранники та двоїсті до них [Архівовано 10 листопада 2017 у Wayback Machine.]
• Stellation and facetting — a Brief History
• Paper Great Icosahedron