Оборотний вузол: відмінності між версіями
| [перевірена версія] | [перевірена версія] |
Створено шляхом перекладу сторінки «Обратимый узел» |
Немає опису редагування |
||
| Рядок 1: | Рядок 1: | ||
В [[Теорія вузлів|теорії вузлів]] '''оборотний вузол''' |
В [[Теорія вузлів|теорії вузлів]] '''оборотний вузол''' — це [[Вузол (математика)|вузол]], який може бути [[ яка охоплює Ізотопія |безперервною деформацією]] переведений у себе, але зі оберненою орієнтацією. '''Необоротний вузол''' — це будь-який вузол, який не має такої властивості. '''Оборотність''' вузла є [[Інваріант вузла|інваріантом вузла]]. '''Оборотне зачеплення''' — це [[Зачеплення (теорія вузлів)|зачеплення]] з такою самою властивістю. |
||
Існує всього п'ять типів симетрії вузлів, які визначаються [[Хіральний вузол|хіральністью]] і оборотністю |
Існує всього п'ять типів симетрії вузлів, які визначаються [[Хіральний вузол|хіральністью]] і оборотністю — повністю хіральний, двосторонній, додатно ахіральний необоротний, від'ємно ахіральний необоротний і повністю ахіральний оборотний{{Sfn|Hoste, Thistlethwaite, Weeks|1998|с=33–48}}. |
||
== Історія питання == |
== Історія питання == |
||
{| class="wikitable" align="center" |
{| class="wikitable" align="center" |
||
|+ Число оборотних і необоротних вузлів за [[Число перетинів (теорія вузлів)|числом перетинів]] |
|+ Число оборотних і необоротних вузлів за [[Число перетинів (теорія вузлів)|числом перетинів]] |
||
! Число перетинів |
! Число перетинів |
||
! 3 |
! 3 |
||
! 4 |
! 4 |
||
! 5 |
! 5 |
||
! 6 |
! 6 |
||
! 7 |
! 7 |
||
! 8 |
! 8 |
||
! 9 |
! 9 |
||
! 10 |
! 10 |
||
! 11 |
! 11 |
||
! 12 |
! 12 |
||
! 13 |
! 13 |
||
! 14 |
! 14 |
||
! 15 |
! 15 |
||
! 16 |
! 16 |
||
! [[Енциклопедія послідовностей цілих чисел|OEIS]] послідовність |
! [[Енциклопедія послідовностей цілих чисел|OEIS]] послідовність |
||
|- align="right" |
|- align="right" |
||
! Необоротні вузли |
! Необоротні вузли |
||
| align="right" | 0 |
| align="right" | 0 |
||
| 0 |
| 0 |
||
| 0 |
| 0 |
||
| 0 |
| 0 |
||
| 0 |
| 0 |
||
| 1 |
| 1 |
||
| 2 |
| 2 |
||
| 33 |
| 33 |
||
| 187 |
| 187 |
||
| 1144 |
| 1144 |
||
| 6919 |
| 6919 |
||
| 38118 |
| 38118 |
||
| 226581 |
| 226581 |
||
| 1309875 |
| 1309875 |
||
| {{OEIS|A052402}} |
| {{OEIS|A052402}} |
||
|- align="right" |
|- align="right" |
||
! Оборотні вузли |
! Оборотні вузли |
||
| 1 |
| 1 |
||
| 1 |
| 1 |
||
| 2 |
| 2 |
||
| 3 |
| 3 |
||
| 7 |
| 7 |
||
| 20 |
| 20 |
||
| 47 |
| 47 |
||
| 132 |
| 132 |
||
| 365 |
| 365 |
||
| 1 032 |
| 1 032 |
||
| 3069 |
| 3069 |
||
| 8854 |
| 8854 |
||
| 26712 |
| 26712 |
||
| 78830 |
| 78830 |
||
| {{OEIS|A052403}} |
| {{OEIS|A052403}} |
||
|} |
|} |
||
Давно відомо, що більшість простих вузлів, таких як [[Трилисник (вузол)|трилисник]] і [[Вісімка (теорія вузлів)|вісімка]], оборотні. [[1962|1962 року]] {{Нп|Ральф Фокс||en|Ralph Fox}} висловив припущення, що деякі вузли необоротні, але не було доведено їх існування, поки в 1963 році {{Нп|Гейл Троттер||en|Hale Trotter}} не виявив нескінченне сімейство необоротних {{Нп|Мереживне зачеплення|мереживних зачеплень|ru|Кружевное зацепление}}{{Sfn|Trotter|1963|с=275–280}}. Тепер відомо, що майже всі вузли необоротні{{Sfn|Murasugi|2007|с=45}}. |
Давно відомо, що більшість простих вузлів, таких як [[Трилисник (вузол)|трилисник]] і [[Вісімка (теорія вузлів)|вісімка]], оборотні. [[1962|1962 року]] {{Нп|Ральф Фокс||en|Ralph Fox}} висловив припущення, що деякі вузли необоротні, але не було доведено їх існування, поки в 1963 році {{Нп|Гейл Троттер||en|Hale Trotter}} не виявив нескінченне сімейство необоротних {{Нп|Мереживне зачеплення|мереживних зачеплень|ru|Кружевное зацепление}}{{Sfn|Trotter|1963|с=275–280}}. Тепер відомо, що майже всі вузли необоротні{{Sfn|Murasugi|2007|с=45}}. |
||
== Оборотні вузли == |
== Оборотні вузли == |
||
[[Файл:Knot-trefoil-dir-128.png|міні|92x92пкс| Найпростіший нетривіальний оборотний вузол, [[Трилисник (вузол)|трилисник]] . Обертання вузла на 180 градусів в 3-вимірному просторі навколо осі на площині малюнка дає той же самий малюнок, але з протилежним напрямком стрілки. ]] |
[[Файл:Knot-trefoil-dir-128.png|міні|92x92пкс| Найпростіший нетривіальний оборотний вузол, [[Трилисник (вузол)|трилисник]] . Обертання вузла на 180 градусів в 3-вимірному просторі навколо осі на площині малюнка дає той же самий малюнок, але з протилежним напрямком стрілки. ]] |
||
Всі вузли з [[Число перетинів (теорія вузлів)|числом перетинів]] 7 і менше |
Всі вузли з [[Число перетинів (теорія вузлів)|числом перетинів]] 7 і менше — оборотні. Не відомо загального методу, який дав би відповідь оборотний вузол чи ні. Проблему можна перевести в алгебричну термінологію{{Sfn|Kuperberg|1996|с=173–181}}, але, на жаль, не відомо алгоритму розв'язання цієї алгебричної задачі. |
||
Якщо вузол оборотний і [[Хіральний вузол|ахіральний]], він повністю ахіральний. Найпростіший вузол з цією властивістю |
Якщо вузол оборотний і [[Хіральний вузол|ахіральний]], він повністю ахіральний. Найпростіший вузол з цією властивістю — вісімка. Хіральні оборотні вузли класифікуються як [[Хіральний вузол#Двосторонній вузол|двосторонні]]{{Sfn|Clark, Elhamdadi, Saito, Yeatman|2013}}. |
||
=== Строго оборотні вузли === |
=== Строго оборотні вузли === |
||
Більш абстрактний спосіб визначення оборотного вузла |
Більш абстрактний спосіб визначення оборотного вузла — сказати, що існує гомеоморфізм 3-сфери, що переводить вузол в себе, але змінює орієнтацію вузла на протилежну. Якщо використовувати замість гомеоморфізму більш строгу умову — [[Інволюція (математика)|інволюцію]] — отримаємо визначення '''строго оборотного''' вузла. Всі вузли з {{Нп|Тунельне число|тунельним числом|en|Tunnel number}} 1, такі як [[Трилисник (вузол)|трилисник]] і [[Вісімка (теорія вузлів)|вісімка]], строго оборотні{{Sfn|Morimoto|1995|с=3527—3532 Лемма 5}}. |
||
== Необоротні вузли == |
== Необоротні вузли == |
||
[[Файл:8_17_Knot.svg|міні|90x90пкс| Вузол 8<sub>17,</sub> найпростіший з необоротних. ]] |
[[Файл:8_17_Knot.svg|міні|90x90пкс| Вузол 8<sub>17,</sub> найпростіший з необоротних. ]] |
||
Найпростішим прикладом необоротного вузла є 8<sub>17</sub> (в позначеннях Александера |
Найпростішим прикладом необоротного вузла є 8<sub>17</sub> (в позначеннях Александера — Бріггса) або .2.2 (в позначеннях Конвея). Мереживний вузол 7, 5, 3 необоротний, як і всі мереживні вузли виду (2 ''p''+1), (2''q''+1), (2''r''+1), де ''p,'' ''q'' і ''r'' — різні цілі, що дає нескінченне сімейство вузлів, необоротність яких довів Троттер{{Sfn|Trotter|1963|с=275—280}}. |
||
== Див. також == |
== Див. також == |
||
| ⚫ | |||
| ⚫ | |||
== Примітки == |
== Примітки == |
||
| Рядок 80: | Рядок 79: | ||
== Література == |
== Література == |
||
* {{статья |
|||
|автор = Jim Hoste, Morwen Thistlethwaite, Jeff Weeks |
|||
|doi = 10.1007/BF03025227 |
|||
|выпуск = 4 |
|||
|издание = The Mathematical Intelligencer |
|||
|mr = 1646740 |
|||
|заглавие = The first 1,701,936 knots |
|||
|url = http://www.math.harvard.edu/~ctm/home/text/class/harvard/101/05/html/home/pdf/first.pdf |
|||
|том = 20 |
|||
|год = 1998 |
|||
|ref = Hoste, Thistlethwaite, Weeks |
|||
|archiveurl = https://web.archive.org/web/20131215102511/http://www.math.harvard.edu/~ctm/home/text/class/harvard/101/05/html/home/pdf/first.pdf |
|||
|archivedate = 2013-12-15 |
|||
}} |
|||
* {{книга-ру |
|||
| автор = H. F. Trotter |
|||
| заглавие= Topology |
|||
| mr = 0158395 |
|||
| вклад= Non-invertible knots exist |
|||
| том = 2 |
|||
| год = 1963 |
|||
| doi=10.1016/0040-9383(63)90011-9 |
|||
|издательство=Pergamon Press |
|||
| ref= Trotter |
|||
}} |
|||
* {{книга-ру |
|||
|заглавие=Knot Theory and Its Applications |
|||
|автор=Kunio Murasugi |
|||
|издательство=Springer |
|||
|год=2007 |
|||
|isbn=9780817647186 |
|||
|url=https://books.google.com/books?id=H2rdoTKwQNMC&pg=PA45 |
|||
|ref= Murasugi |
|||
}} |
|||
* {{статья |
|||
| автор = Greg Kuperberg |
|||
| arxiv = q-alg/9712048 |
|||
| doi = 10.1142/S021821659600014X |
|||
| выпуск = 2 |
|||
| издание = Journal of Knot Theory and its Ramifications |
|||
| mr = 1395778 |
|||
| заглавие = Detecting knot invertibility |
|||
| том = 5 |
|||
| год = 1996 |
|||
| ref= Kuperberg |
|||
}} |
|||
* {{статья |
|||
| автор = W. Edwin Clark, Mohamed Elhamdadi, Masahico Saito, Timothy Yeatman |
|||
| arxiv = 1312.3307 |
|||
| заглавие = Quandle colorings of knots and applications |
|||
| год = 2013 |
|||
| ref= Clark, Elhamdadi, Saito, Yeatman |
|||
}} |
|||
* {{статья |
|||
| автор = Kanji Morimoto |
|||
| doi = 10.1090/S0002-9939-1995-1317043-4 |
|||
| выпуск = 11 |
|||
| издание = Proceedings of the American Mathematical Society |
|||
| jstor = 2161103 |
|||
| mr = 1317043 |
|||
| заглавие = There are knots whose tunnel numbers go down under connected sum |
|||
| том = 123 |
|||
| год = 1995 |
|||
| ref= Morimoto |
|||
}} |
|||
== Посилання == |
== Посилання == |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
{{Теорія вузлів}} |
{{Теорія вузлів}} |
||
[[Категорія:Теорія вузлів]] |
[[Категорія:Теорія вузлів]] |
||
Версія за 07:48, 19 серпня 2020
В теорії вузлів оборотний вузол — це вузол, який може бути безперервною деформацією переведений у себе, але зі оберненою орієнтацією. Необоротний вузол — це будь-який вузол, який не має такої властивості. Оборотність вузла є інваріантом вузла. Оборотне зачеплення — це зачеплення з такою самою властивістю.
Існує всього п'ять типів симетрії вузлів, які визначаються хіральністью і оборотністю — повністю хіральний, двосторонній, додатно ахіральний необоротний, від'ємно ахіральний необоротний і повністю ахіральний оборотний[1].
Історія питання
| Число перетинів | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | OEIS послідовність |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Необоротні вузли | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 33 | 187 | 1144 | 6919 | 38118 | 226581 | 1309875 | послідовність A052402 з Онлайн енциклопедії послідовностей цілих чисел, OEIS |
| Оборотні вузли | 1 | 1 | 2 | 3 | 7 | 20 | 47 | 132 | 365 | 1 032 | 3069 | 8854 | 26712 | 78830 | послідовність A052403 з Онлайн енциклопедії послідовностей цілих чисел, OEIS |
Давно відомо, що більшість простих вузлів, таких як трилисник і вісімка, оборотні. 1962 року Ральф Фокс[en] висловив припущення, що деякі вузли необоротні, але не було доведено їх існування, поки в 1963 році Гейл Троттер[en] не виявив нескінченне сімейство необоротних мереживних зачеплень[2]. Тепер відомо, що майже всі вузли необоротні[3].
Оборотні вузли
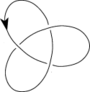
Всі вузли з числом перетинів 7 і менше — оборотні. Не відомо загального методу, який дав би відповідь оборотний вузол чи ні. Проблему можна перевести в алгебричну термінологію[4], але, на жаль, не відомо алгоритму розв'язання цієї алгебричної задачі.
Якщо вузол оборотний і ахіральний, він повністю ахіральний. Найпростіший вузол з цією властивістю — вісімка. Хіральні оборотні вузли класифікуються як двосторонні[5].
Строго оборотні вузли
Більш абстрактний спосіб визначення оборотного вузла — сказати, що існує гомеоморфізм 3-сфери, що переводить вузол в себе, але змінює орієнтацію вузла на протилежну. Якщо використовувати замість гомеоморфізму більш строгу умову — інволюцію — отримаємо визначення строго оборотного вузла. Всі вузли з тунельним числом[en] 1, такі як трилисник і вісімка, строго оборотні[6].
Необоротні вузли

Найпростішим прикладом необоротного вузла є 817 (в позначеннях Александера — Бріггса) або .2.2 (в позначеннях Конвея). Мереживний вузол 7, 5, 3 необоротний, як і всі мереживні вузли виду (2 p+1), (2q+1), (2r+1), де p, q і r — різні цілі, що дає нескінченне сімейство вузлів, необоротність яких довів Троттер[7].
Див. також
Примітки
- ↑ Hoste, Thistlethwaite, Weeks, 1998, с. 33–48.
- ↑ Trotter, 1963, с. 275–280.
- ↑ Murasugi, 2007, с. 45.
- ↑ Kuperberg, 1996, с. 173–181.
- ↑ Clark, Elhamdadi, Saito, Yeatman, 2013.
- ↑ Morimoto, 1995, с. 3527—3532 Лемма 5.
- ↑ Trotter, 1963, с. 275—280.
Література
- Jim Hoste, Morwen Thistlethwaite, Jeff Weeks. The first 1,701,936 knots : [арх. 15 грудня 2013] // The Mathematical Intelligencer. — 1998. — Т. 20, вип. 4. — DOI:10.1007/BF03025227.
- H. F. Trotter. Topology. — Pergamon Press, 1963. — Т. 2. — DOI:10.1016/0040-9383(63)90011-9.
- Kunio Murasugi. Knot Theory and Its Applications. — Springer, 2007. — ISBN 9780817647186.
- Greg Kuperberg. Detecting knot invertibility // Journal of Knot Theory and its Ramifications. — 1996. — Т. 5, вип. 2. — arXiv:q-alg/9712048. — DOI:10.1142/S021821659600014X.
- W. Edwin Clark, Mohamed Elhamdadi, Masahico Saito, Timothy Yeatman. Quandle colorings of knots and applications. — 2013. — arXiv:1312.3307.
- Kanji Morimoto. There are knots whose tunnel numbers go down under connected sum // Proceedings of the American Mathematical Society. — 1995. — Т. 123, вип. 11. — DOI:10.1090/S0002-9939-1995-1317043-4. — JSTOR 2161103.
Посилання
- Jablan, Slavik & Sazdanovic, Radmila. Basic graph theory: Non-invertible knot and links, LinKnot.(англ.)
- Explanation with a video, Nrich. Maths.org.
| ||||||||||||||||||||||||||||