Драбина Мебіуса

Два подання драбини Мебіуса $M_{16}$.

Анімація перетворення одного виду в інший

Подання драбини Мебіуса M₁₆ у вигляді стрічки Мебіуса.

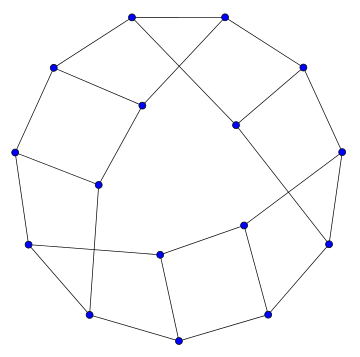
Драби́на Ме́біуса $M_{n}$ — кубічний циркулянтний граф з парним числом вершин $n$, утворений з циклу з $n$ вершинами шляхом додавання ребер (званих «щаблями»), що з'єднують протилежні пари вершин циклу. Названий так через те, що $M_{n}$ складається з $n/2$ циклів довжини 4, з'єднаних разом спільними ребрами, які утворюють топологічно стрічку Мебіуса. Повний двочастковий граф $K_{3,3}$ (граф «Вода, газ та електрика») є драбиною Мебіуса $M_{6}$ (на відміну від інших $M_{6}$ має додаткові цикли довжини 4).

Якщо $n\equiv 2{\pmod {4}}$, то $M_{n}$ є двочастковим. При $n\equiv 2{\pmod {4}}$ за теоремою Брукса хроматичне число $M_{n}$ дорівнює 3. Відомо, що драбина Мебіуса однозначно визначається її многочленом Татта.

Властивості

Будь-які сходи Мебіуса є непланарним верхівковим графом. Число схрещень драбини Мебіуса дорівнює одиниці, і граф можна вкласти без самоперетинів у тор або проєктивну площину (тобто є тороїдальним графом). Лі вивчив вкладення цих графів у поверхні більш високих родів.

Драбини Мебіуса є вершинно-транзитивними, але (за винятком $M_{6}$) не реберно-транзитивними — кожне ребро циклу, з якого драбину утворено, належить єдиному 4-реберному циклу, тоді як кожна перекладина належить двом таким циклам.

Драбина Мебіуса $M_{8}$ має 392 кістякових дерева. Цей граф і $M_{6}$ мають найбільше число кістякових дерев серед кубічних графів з тим самим числом вершин. Однак серед кубічних графів з 10 вершинами найбільше число кістякових дерев має граф Петерсена, який не є драбиною Мебіуса.

Многочлени Татта драбин Мебіуса можна отримати за простою рекурентною формулою.

Мінори графа

Граф Вагнера $M_{8}$

Драбини Мебіуса відіграють важливу роль у теорії мінорів графа. Найранішим результатом такого типу є теорема Вагнера про те, що граф, який не містить $K_{5}$-мінорів, можна утворити з використанням сум за клікою для комбінування планарних графів і драбини Мебіуса $M_{8}$ (через це $M_{n}$ називають графом Вагнера.

Всі 3-зв'язні майже-планарні графи є драбинами Мебіуса або належать невеликого числа інших сімейств, причому решту майже-планарних графів можна отримати з цих графів за допомогою низки простих операцій.

Майже всі^{[уточнити]} графи, які не містять куба як мінора, можна отримати з драбини Мебіуса послідовним застосуванням простих операцій.

Хімія і фізика

В 1982 році синтезовано молекулярну структуру, що має форму сходів Мебіуса, і відтоді такі графи становлять інтерес для хіміків і хімічної стереографії, зокрема через схожість на драбину Мебіуса молекул ДНК. Зважаючи на це, особливо вивчено математичні симетрії вкладень драбин Мебіуса в $\mathbb {R} ^{3}$.

Драбини Мебіуса використовують як модель надпровідного кільця в експериментах з вивчення ефектів топології провідності при взаємодії електронів.

Комбінаторна оптимізація

Драбини Мебіуса використовують також в інформатиці в межах підходу цілочисельного програмування до задач пакування множин і лінійного впорядкування. Деякі конфігурації в цих задачах можна використати для визначення граней політопів, що описують ослаблення умов лінійного програмування. Ці грані називають обмеженнями драбин Мебіуса.

Див. також

• Стрічка Мебіуса
• Дивна петля
• Пляшка Кляйна
• Граф-драбина

Література

• N. L. Biggs, R. M. Damerell, D. A. Sands. Recursive families of graphs // Journal of Combinatorial Theory. — 1972. — Т. 12 (13 травня). — С. 123–131. — (Series B). — DOI:10.1016/0095-8956(72)90016-0.
• G. Bolotashvili, M. Kovalev, E. Girlich. New facets of the linear ordering polytope // SIAM Journal on Discrete Mathematics. — 1999. — Т. 12, вип. 3 (13 травня). — С. 326–336. — DOI:10.1137/S0895480196300145.
• Ralf Borndörfer, Robert Weismantel. Set packing relaxations of some integer programs // Mathematical Programming. — 2000. — Т. 88, вип. 3 (13 травня). — С. 425–450. — (Series A). — DOI:10.1007/PL00011381.
• Wen-Ji Deng, Ji-Huan Xu, Ping Liu. Period halving of persistent currents in mesoscopic Möbius ladders // Chinese Physics Letters. — 2002. — Т. 19, вип. 7 (13 травня). — С. 988–991. — arXiv:cond-mat/0209421. — DOI:10.1088/0256-307X/19/7/333.
• Erica Flapan. Symmetries of Möbius ladders // Mathematische Annalen. — 1989. — Т. 283, вип. 2 (13 травня). — С. 271–283. — DOI:10.1007/BF01446435.
• M. Grötschel, M. Jünger, G. Reinelt. On the acyclic subgraph polytope // Mathematical Programming. — 1985. — Т. 33 (13 травня). — С. 28–42. — DOI:10.1007/BF01582009.
• M. Grötschel, M. Jünger, G. Reinelt. Facets of the linear ordering polytope // Mathematical Programming. — 1985. — Т. 33 (13 травня). — С. 43–60. — DOI:10.1007/BF01582010.
• Bradley S. Gubser. A characterization of almost-planar graphs // Combinatorics, Probability and Computing. — 1996. — Т. 5, вип. 3 (13 травня). — С. 227–245. — DOI:10.1017/S0963548300002005.
• Richard K. Guy, Frank Harary. On the Möbius ladders // Canadian Mathematical Bulletin. — 1967. — Т. 10 (13 травня). — С. 493–496. — DOI:10.4153/CMB-1967-046-4.
• Dmitry Jakobson, Igor Rivin. On some extremal problems in graph theory. — 1999. — 13 травня. — arXiv:math.CO/9907050.
• De-ming Li. Genus distributions of Möbius ladders // Northeastern Mathematics Journal. — 2005. — Т. 21, вип. 1 (13 травня). — С. 70–80.
• John Maharry. A characterization of graphs with no cube minor // Journal of Combinatorial Theory. — 2000. — Т. 80, вип. 2 (13 травня). — С. 179–201. — (Series B). — DOI:10.1006/jctb.2000.1968.
• John P. McSorley. Counting structures in the Möbius ladder // Discrete Mathematics. — 1998. — Т. 184, вип. 1–3 (13 травня). — С. 137–164. — DOI:10.1016/S0012-365X(97)00086-1.
• Anna De Mier, Marc Noy. On graphs determined by their Tutte polynomials // Graphs and Combinatorics. — 2004. — Т. 20, вип. 1 (13 травня). — С. 105–119. — DOI:10.1007/s00373-003-0534-z.
• Frédéric Mila, C. A. Stafford, Sylvain Capponi. Persistent currents in a Möbius ladder: A test of interchain coherence of interacting electrons // Physical Review B. — 1998. — Т. 57, вип. 3 (13 травня). — С. 1457–1460. — DOI:10.1103/PhysRevB.57.1457. Архівовано з джерела 20 січня 2022. Процитовано 22 листопада 2020.
• Alantha Newman, Santosh Vempala. [1] — Berlin : Springer-Verlag, 2001. — Т. 2081. — С. 333–347. — (Lecture Notes in Computer Science) — DOI:10.1007/3-540-45535-3_26. Архівовано з джерела 2 січня 2004
• Jonathan Simon. New scientific applications of geometry and topology (Baltimore, MD, 1992). — Providence, RI : American Mathematical Society, 1992. — Т. 45. — С. 97–130. — (Proceedings of Symposia in Applied Mathematics)
• L. Valdes. Proceedings of the Twenty-second Southeastern Conference on Combinatorics, Graph Theory, and Computing (Baton Rouge, LA, 1991). — 1991. — Т. 85. — С. 143–160. — (Congressus Numerantium)
• K. Wagner. Über eine Eigenschaft der ebenen Komplexe // Mathematische Annalen. — 1937. — Т. 114 (13 травня). — С. 570–590. — DOI:10.1007/BF01594196.
• D. Walba, R. Richards, R. C. Haltiwanger. Total synthesis of the first molecular Möbius strip // Journal of the American Chemical Society. — 1982. — Т. 104, вип. 11 (13 травня). — С. 3219–3221. — DOI:10.1021/ja00375a051.

Посилання

• Weisstein, Eric W. Драбина Мебіуса(англ.) на сайті Wolfram MathWorld.