Стрічка Мебіуса

Стрічка Мебіуса у інтерпретації Ешера

Стрі́чка Ме́біуса чи Смужка (Лист) Мебіуса (німецька вимова [ˈmøbiʊs]) є поверхнею лише з однією стороною і лише однією границею. Вона має математичну властивість неорієнтованості. Також вона є лінійчатою поверхнею. Вона була незалежно відкрита Німецькими математиками Мебіусом і Лістінгом в 1858 році.

Її екземпляр легко може бути виготовлений зі смужки паперу, повертаючи один з їй кінців на півоберту і з'єднуючи кінці стрічки для створення замкненої поверхні. В Евклідовому просторі є два типи стрічок Мебіуса, в залежності від напряму здійсненого півоберту: за годинниковою стрілкою, та проти. Звідси можна зробити висновок, що стрічка Мебуіса є хіральною.

Рівняння

Параметричний опис стрічки Мебіуса.

Як поверхня в $\R^3$, стрічка Мебіуса задається параметричним рівнянням:

$x (u, v) = \left (1 +\frac {v} {2} \cos\frac {u} {2} \right) \cos u,$

$y (u, v) = \left (1 +\frac {v} {2} \cos\frac {u} {2} \right) \sin u,$

$z (u, v) = \frac {v} {2} \sin\frac {u} {2},$

где $0\leqslant u <2\pi$ та $-1\leqslant v\leqslant 1$. Ці формули задають стрічку Мебіуса ширини 1, чий центральний круг має радіус 1 та лежить у площині $Oxy\ (z=0)$ з центром в точці $(0,\;0,\;0)$. Параметр $u$ пробігає вздовж стрічки, в той час як $v$ задає відстань від краю.

В циліндричних координатах $(r,\;\theta,\;z)$, необмежена версія листа Мебіуса може бути представлена рівнянням:

$~\log r \sin (\theta/2) = z \cos (\theta/2),$

де функція логарифма має довільне основу.

Властивості

Стрічка Мебіуса має цікаві властивості. Якщо спробувати розрізати стрічку по лінії, рівновіддаленій від країв, то замість двох стрічок Мебіуса утвориться одна довга, двостороння, в два рази більш закручена стрічка. Якщо тепер цю стрічку ще раз так само розрізати, то утворяться дві стрічки, намотані одна на одну.

• 

  Стрічка Мебіуса зроблена зі смужки паперу або стрічки.

• 

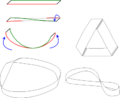
  Щоб перетворити прямокутник в стрічку Мебіуса, з'єднайте ребра, позначені "A" так, щоб напрями стрілок збіглися.

• 

  Схема створення стрічки Мебіуса зі стрічки папіру

Символіка

Міжнародний символ переробки.

У 20 столітті бузкова стрічка Мебіуса стала символом немоногамних стосунків та вільного кохання зокрема.

Див. також

• Пляшка Клейна
• Перетворення Мебіуса
• Резистор Мебіуса