Надлишковий код
Надлишковий код[1] (англ. Erasure code) — в теорії кодування завадостійкий код[1], здатний відновити цілі пакети даних у разі їх втрати[2]. Такий код дозволяє боротися з витоками даних під час передачі каналами зв'язку або роботі з пам'яттю. Зазвичай він використовується, коли точна позиція втрачених даних відома апріорі[3].
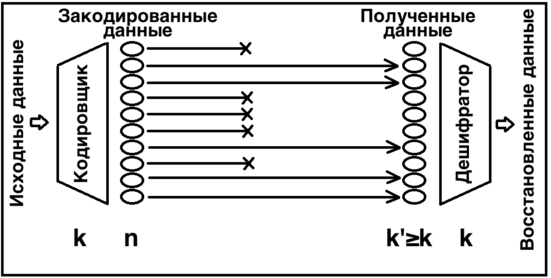
Принцип роботи[ред. | ред. код]
Надлишковий код перетворює повідомлення з символів у довше повідомлення (кодове слово) з символів так, що вихідне повідомлення може бути відновлено за будь-якими символами. Такий код називається кодом, вираз — кодовою часткою[4], вираз — ефективністю прийому[5][6].
Надлишковий код зазвичай використовується на верхніх рівнях стека протоколів каналів передачі та зберігання інформації[3].
Оптимальний надлишковий код[ред. | ред. код]
Оптимальний надлишковий код відрізняється тим, що будь-яких з символів кодового слова достатньо для відновлення вихідного повідомлення[7], тобто вони мають оптимальну ефективність прийому[5][8].
Перевірка парності[ред. | ред. код]
Розглянемо випадок, коли . За допомогою набору з значень обчислюється контрольна сума та додається до вихідних значеннь:
- .
Тепер у набір з значень включено контрольну суму. У разі втрати одного із значень , його можна буде з легкістю відновити за допомогою підсумовування:
- .
Більш складні комбінації шуканих і отримуваних значень є Граф Таннера[en][4][5].
Лінійний код[ред. | ред. код]
Важливим підкласом надлишкового коду є лінійний код. Його назва пов'язана з тим, що він може бути проаналізований за допомогою лінійної алгебри. Нехай — вихідні дані, — матриця розміру тоді закодовані дані — коди можуть бути представлені як . Припустимо, що приймач отримав компонент вектора , тоді вихідні дані можуть бути відновлені за допомогою рівнянь, пов'язаних із відомими компонентами вектора . Нехай матриця розміру відповідає цій системі рівнянь. Відновлення можливе, якщо всі ці рівняння лінійно незалежні і в загальному випадку це означає, що будь-яка матриця розміру оборотна. Матриця називається генеруючою матрицею коду, тому що будь-який допустимий може бути отриманий як лінійна комбінація стовпців матриці . Оскільки її ранг дорівнює , то будь-яка підмножина з закодованих елементів має містити інформацію про всі вихідних даних. Для отримання вихідних даних необхідно вирішити лінійну систему: , де — підмножина з елементів вектора , доступних на приймачі[9].
Поліноміальна передискретизація[ред. | ред. код]
Приклад: Несправна електронна пошта (англ. Faulty e-mail)[ред. | ред. код]
У випадку, коли надлишкові символи можуть бути створені як проміжні точки на відрізку, що з'єднує два вихідні символи. Це показано на простому прикладі, який називається несправною електронною поштою:

Аліса хоче надіслати свій телефонний номер (555629) Бобу, використовуючи несправну електронну пошту. Цей вид пошти працює так само, як звичайна електронна пошта, за таким винятком:
- Близько половини всіх повідомлень губляться.
- Повідомлення довші за 5 символів заборонені.
- Це дуже дорого.
Замість того, щоб запитати у Боба підтвердження повідомлення, яке вона надіслала, Аліса вигадує таку схему:
- Вона розбиває свій телефонний номер на дві частини і надсилає 2 повідомлення Бобу — «A = 555» і «B = 629»
- Вона будує лінійну функцію , у цьому прикладі . Таким чином і .
- Вона вважає значення і , а потім відправляє три надлишкові повідомлення: «C=703», «D=777» і «E=851».
Боб знає, що вираз для наступне , де і — дві частини телефонного номера. Тепер припустимо, що Боб отримує «D = 777» і «E = 851».

Боб може відновити телефонний номер Аліси за допомогою і , використовуючи значення і , які він отримав. Більш того, він може це зробити, використовуючи два будь-які отримані повідомлення. Отже, у цьому прикладі кодова частка дорівнює 40 %. Зауважимо, що Аліса не може закодувати свій номер телефону лише в одному повідомленні такої пошти, оскільки він складається з 6 символів, а максимальна довжина одного повідомлення — 5 символів. Якби вона відправляла свій номер телефону частинами, запитуючи підтвердження кожної частини від Боба, то було б відправлено мінімум 4 повідомлення (два від Аліси і два підтвердження від Боба)[5][10].
Загальний випадок[ред. | ред. код]
Наведена вище лінійна конструкція може бути узагальнена до поліноміальної інтерполяції. У такому разі крапки тепер обчислюються над кінцевим полем , де — число біт у символі. Відправник нумерує символи даних від до і посилає їх. Потім він будує, наприклад, інтерполяційний многочлен Лагранжа степеня , так що дорівнює -ому символу даних. Потім він відправляє . За допомогою поліноміальної інтерполяції одержувач зможе відновити втрачені дані у разі, якщо він успішно прийняв символів[5].
Реалізація у реальному світі[ред. | ред. код]
Цей процес реалізований у Коді Ріда — Соломона з кодовими словами, сконструйованими над кінцевим полем при використанні визначника Вандермонда[11].
Майже оптимальний надлишковий код[ред. | ред. код]
Майже оптимальний надлишковий код вимагає символів, щоб відновити повідомлення (де ). Величина може бути зменшена за рахунок додаткового часу роботи процесора. При використанні таких кодів необхідно вирішити, що краще: складність обчислень або можливість корекції повідомлень[11]. У 2004 році існував тільки один майже оптимальний надлишковий код з лінійним часом кодування та декодування — код Торнадо[en][8].
Застосування[ред. | ред. код]
Надлишкові коди застосовуються в[11]:
- Reliable Multicast[en] (наприклад, у групі з надійного мультимовлення IETF)
- 3GPP (MBMS та eMBMS (Multimedia Broadcast Multicast Service[en])
- однорангові мережі, наприклад, для вирішення проблеми передачі останнього блоку даних
- Розподільні сховища.
Приклади[ред. | ред. код]
Тут наведено деякі приклади різних кодів.
- Майже оптимальні надлишкові коди
- Оптимальні надлишкові коди
Примітки[ред. | ред. код]
- ↑ а б Шинкаренко К.В., Кориков A.M. Помехоустойчивое кодирование мультимедиа данных в компьютерных сетях // Известия Томского политехнического университета [Известия ТПУ] : журнал. — 2008. — Т. 313, № 5, Число 29 (сентябрь). — С. 37—41. — ISSN 1684-8519. Архівовано з джерела 31 січня 2022. Процитовано 31 січня 2022.
- ↑ Шинкаренко Константин Всеволодович, Кориков Анатолий Михайлович. Исследование эффективности помехоустойчивых кодов Лаби // Доклады Томского государственного университета систем управления и радиоэлектроники : журнал. — 2009. — 5 мая. — С. 185-192. Архівовано з джерела 11 грудня 2019. Процитовано 31 січня 2022.
- ↑ а б Katina Kralevska. Applied Erasure Coding in Networks and Distributed Storage // ResearchGate : thesis for the degree of Philosophiae Doctor. — 2018. — Март. — P. 7. Архівовано з джерела 31 січня 2022. Процитовано 31 січня 2022.
- ↑ а б J.S. Plank ; A.L. Buchsbaum ; R.L. Collins ; M.G. Thomason. Small parity-check erasure codes - exploration and observations // 2005 International Conference on Dependable Systems and Networks (DSN'05) : conference. — 2005. — . — Июль. — P. 2. — ISSN 1530-0889. Архівовано з джерела 31 січня 2022. Процитовано 31 січня 2022.
- ↑ а б в г д Dave K. Kythe, Prem K. Kythe. Algebraic and Stochastic Coding Theory. — 1-е изд. — CRC Press, 2012. — С. 377—378. — ISBN 978-1439881811.
- ↑ Alexandros G. Dimakis, P. Brighten Godfrey, Martin J. Wainwright and Kannan Ramchandran. Network Coding for Distributed Storage Systems // IEEE Transactions on Information Theory : journal. — 2007. — Vol. 56, no. 9, (Август). — P. 4539—4551. — ISSN 0018-9448. — DOI:. Архівовано з джерела 31 січня 2022. Процитовано 31 січня 2022.
- ↑ N. Alon ; J. Edmonds ; M. Luby. Linear time erasure codes with nearly optimal recovery // Proceedings of IEEE 36th Annual Foundations of Computer Science : symposium. — 1995. — . — Октябрь. — P. 1. — ISSN 0272-5428. — DOI:. Архівовано з джерела 31 січня 2022. Процитовано 31 січня 2022.
- ↑ а б Petar Maymounkov, David Mazi`eres. Rateless Codes And Big Downloads // 2nd International Workshop on Peer-to-Peer Systems : conference. — 2004. — Vol. 2735 (Август). — P. 2. — DOI:. Архівовано з джерела 31 січня 2022. Процитовано 31 січня 2022.
- ↑ Luigi Rizzo. Effective Erasure Codes for Reliable Computer Communication Protocols // ACM SIGCOMM Computer Communication Review : newsletter. — 1997. — Vol. 27, no. 2 (Апрель). — P. 24—36. — DOI:. Архівовано з джерела 13 березня 2022. Процитовано 31 січня 2022.
- ↑ Hamid Jafarkhani, Mahdi Hajiaghayi (22.10.2015). United States Patent Application Publication (PDF). COST-EFFICIENT REPAIR FOR STORAGE SYSTEMS USING PROGRESSIVE ENGAGEMENT. The Regents of the University of California,Oakland,CA (US). с. 1. Архів оригіналу (PDF) за 4 травня 2022. Процитовано 31 січня 2022.
- ↑ а б в Dave K.Kythe, Prem K. Kythe. Algebraic and Stochastic Coding Theory. — 1-е изд. — CRC Press,, 2012. — С. 380—381. — ISBN 978-1439881811.
Література[ред. | ред. код]
- Dave K. Kythe, Prem K. Kythe. Algebraic and Stochastic Coding Theory. — 1-е изд. — CRC Press, 2012. — С. 375—395. — ISBN 978-1439881811.















































