Надлишковий код: відмінності між версіями

Вилучено вміст Додано вміст

Лінійно

Версія за 16:37, 31 січня 2022

Стираючий код^[1] (англ. Erasure code) - Теоретично кодування завадостійкий код^[1], здатний відновити цілі пакети даних у разі їх втрати^[2]. Такий код дозволяє боротися з витоками даних під час передачі каналами зв'язку або роботи з пам'яттю. Зазвичай він використовується, коли точна позиція втрачених даних відома апріорі^[3].

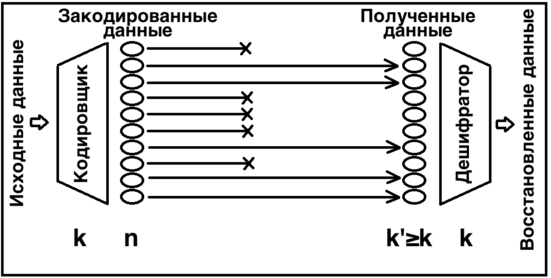
Принцип роботи

Стираючий код перетворює повідомлення з $k$ символів у довше повідомлення (кодове слово) з $n$ символів так, що вихідне повідомлення може бути відновлено за $k'$ будь-яким символам. Такий код називається $(n,k)$ кодом, вираз $r=k/n$ - кодовою часткою^[4], вираз $k'/k$ - Ефективністю прийому^[5]^[6].

Стираючий код зазвичай використовується на верхніх рівнях стека протоколів каналів передачі та зберігання інформації^[3].

Оптимальний пральний код

Оптимальний стираючий відрізняється тим, що будь-яких $k$ з $n$ символів кодового слова достатньо відновлення вихідного повідомлення^[7], тобто вони мають оптимальну ефективність прийому^[5]^[8].

Перевірка парності

Розглянемо випадок, коли $n=k+1$ . За допомогою набору з $k$ значень $\{v_{i}\}_{1\leq i\leq k}$ обчислюється контрольна сума та додається до $k$ вихідним значенням:

v_{k+1}=-\sum _{i=1}^{k}v_{i}

.

Тепер у набір $\{v_{i}\}_{1\leq i\leq k+1}$ з $k+1$ значень включено контрольну суму. У разі втрати одного зі значень $v_{e}$ , його можна буде з легкістю відновити за допомогою підсумовування:

v_{e}=-\sum _{i=1,i\neq e}^{k+1}v_{i}

.

Більш складні комбінації шуканих і отримуваних значень є Граф Таннера^[4]^[5].

Лінійний код

Важливим підкласом стирального коду є лінійний код. Його назва пов'язана з тим, що він може бути проаналізований за допомогою лінійної алгебри. Нехай $x=x_{0}\dots x_{k-1}$ - вихідні дані, $G$ - матриця розміру $n\times k$ тоді закодовані дані $(n,k)$ - коди можуть бути представлені як ${\vec {y}}=G{\vec {x}}$ . Припустимо, що приймач отримав $k$ компонент вектора ${\vec {y}}$ , тоді вихідні дані можуть бути відновлені за допомогою $k$ рівнянь, пов'язаних із відомими компонентами вектора ${\vec {y}}$ . Нехай матриця $G'$ розміру $k\times k$ відповідає цій системі рівнянь. Відновлення можливе, якщо всі ці рівняння лінійно незалежні і в загальному випадку це означає, що будь-яка матриця розміру $k\times k$ оборотна. Матриця $G$ називається генеруючою матрицею коду, тому що будь-який допустимий ${\vec {y}}$ може бути отриманий як лінійна комбінація стовпців матриці $G$ . Оскільки її ранг дорівнює $k$ , то будь-яка підмножина з $k$ закодованих елементів має містити інформацію про всіх $k$ вихідних даних. Для отримання вихідних даних необхідно вирішити лінійну систему: ${\vec {y'}}=G'{\vec {x}}$ , де ${\vec {y'}}$ - підмножина з $k$ елементів векторного ${\vec {y}}$ , доступних на приймачі^[9].

Поліноміальна передискретизація

Приклад: Несправна електронна пошта (англ. Faulty e-mail

У випадку, коли $k=2$ надлишкові символи можуть бути створені як проміжні точки на відрізку, що з'єднує два вихідні символи. Це показано на простому прикладі, який називається несправною електронною поштою:

Аліса хоче надіслати свій телефонний номер (555629) Бобу, використовуючи несправну електронну пошту. Цей вид пошти працює так само, як звичайна електронна пошта, за таким винятком:

Близько половини всіх повідомлень губляться.
Повідомлення довші за 5 символів заборонені.
Це дуже дорого.

Замість того, щоб запитати у Боба підтвердження повідомлення, яке вона надіслала, Аліса вигадує таку схему:

Вона розбиває свій телефонний номер на дві частини $a=555,b=629$ і надсилає 2 повідомлення Бобу - "A = 555" і "B = 629"
Вона будує лінійну функцію $f(i)=a+(b-a)(i-1)$ , у цьому прикладі $f(i)=555+74(i-1)$ . Таким чином $f(1)=555$ і $f(2)=629$ .
Вона вважає значення $f(3)=703,f(4)=777$ і $f(5)=851$ , а потім відправляє три надлишкові повідомлення: C=703, D=777 і E=851

Боб знає, що вираз для $f(k)$ наступне $f(i)=a+(b-a)(i-1)$ , де $a$ і $b$ - Дві частини телефонного номера. Тепер припустимо, що Боб отримує "D = 777" і "E = 851".

Боб може відновити телефонний номер Аліси за допомогою $a$ і $b$ , використовуючи значення $f(4)$ і $f(5)$ , які він отримав. Більш того, він може це зробити, використовуючи два будь-які отримані повідомлення. Отже, у цьому прикладі кодова частка дорівнює 40%. Зауважимо, що Аліса не може закодувати свій номер телефону лише в одному повідомленні такої пошти, оскільки він складається з 6 символів, а максимальна довжина одного повідомлення – 5 символів. Якби вона відправляла свій номер телефону частинами, запитуючи підтвердження кожної частини від Боба, то було б відправлено мінімум 4 повідомлення (два від Аліси і два підтвердження від Боба)^[5]^[10].

Загальний випадок

Наведена вище лінійна конструкція може бути узагальнена до поліноміальної інтерполяції. У такому разі крапки тепер обчислюються над кінцевим полем $\mathbb {F} _{2^{m}}$ , де $m$ - Число біт у символі. Відправник нумерує символи даних від $0$ до $k-1$ і посилає їх. Потім він будує, наприклад, інтерполяційний багаточлен Лагранжа $p(x)$ ступеня $k$ , так що $p(i)$ дорівнює $i$ -ого символу даних. Потім він відправляє $p(k),\ldots ,p(n-1)$ . За допомогою поліноміальної інтерполяції одержувач зможе відновити втрачені дані у разі, якщо він успішно прийняв $k$ символів^[5].

Реалізація у реальному світі

Цей процес реалізований у Коді Ріда - Соломона з кодовими словами, сконструйованими над кінцевим полем при використанні визначника Вандермонда^[11].

Майже оптимальний стиральний код

Майже оптимальний пральний код вимагає $(1+\varepsilon )k$ символів, щоб відновити повідомлення (де $\varepsilon >0$ ). Величина $\varepsilon$ може бути зменшена рахунок додаткового часу роботи процесора. При використанні таких кодів необхідно вирішити, що краще: складність обчислень або можливість корекції повідомлень^[11]. У 2004 році існував тільки один майже оптимальний пральний код з лінійним часом кодування та декодування - код Торнадо^[en]^[8].

Застосування

Стиральні коди застосовуються в^[11]:

Reliable Multicast^[en] (наприклад, у групі з надійного мультимовлення IETF)
3GPP (MBMS та eMBMS (Multimedia Broadcast Multicast Service^[en])
однорангові мережі, наприклад, для вирішення проблеми передачі останнього блоку даних
Распределённых хранилищах^[en].

Приклади

Тут наведено деякі приклади різних кодів.

Майже оптимальні пральні коди

Код із малою щільністю перевірок на парність

Оптимальні пральні коди

Примітки

↑ ^а ^б Шинкаренко К.В., Кориков A.M. Помехоустойчивое кодирование мультимедиа данных в компьютерных сетях // Известия Томского политехнического университета [Известия ТПУ] : журнал. — 2008. — Т. 313, № 5, Число 29 (сентябрь). — С. 37—41. — ISSN 1684-8519.
↑ Шинкаренко Константин Всеволодович, Кориков Анатолий Михайлович. Исследование эффективности помехоустойчивых кодов Лаби // Доклады Томского государственного университета систем управления и радиоэлектроники : журнал. — 2009. — 17 мая. — С. 185-192.
↑ ^а ^б Katina Kralevska. Applied Erasure Coding in Networks and Distributed Storage // ResearchGate : thesis for the degree of Philosophiae Doctor. — 2018. — Март. — P. 7.
↑ ^а ^б J.S. Plank ; A.L. Buchsbaum ; R.L. Collins ; M.G. Thomason. Small parity-check erasure codes - exploration and observations // 2005 International Conference on Dependable Systems and Networks (DSN'05) : conference. — 2005. — . — Июль. — P. 2. — ISSN 1530-0889.
↑ ^а ^б ^в ^г ^д Dave K. Kythe, Prem K. Kythe. Algebraic and Stochastic Coding Theory. — 1-е изд. — CRC Press, 2012. — С. 377—378. — ISBN 978-1439881811.
↑ Alexandros G. Dimakis, P. Brighten Godfrey, Martin J. Wainwright and Kannan Ramchandran. Network Coding for Distributed Storage Systems // IEEE Transactions on Information Theory : journal. — 2007. — Vol. 56, no. 9, (Август). — P. 4539—4551. — ISSN 0018-9448. — DOI:10.1109/TIT.2010.2054295.
↑ N. Alon ; J. Edmonds ; M. Luby. Linear time erasure codes with nearly optimal recovery // Proceedings of IEEE 36th Annual Foundations of Computer Science : symposium. — 1995. — . — Октябрь. — P. 1. — ISSN 0272-5428. — DOI:10.1109/SFCS.1995.492581.
↑ ^а ^б Petar Maymounkov, David Mazi`eres. Rateless Codes And Big Downloads // 2nd International Workshop on Peer-to-Peer Systems : conference. — 2004. — Vol. 2735 (Август). — P. 2. — DOI:10.1007/978-3-540-45172-3_23.
↑ Luigi Rizzo. Effective Erasure Codes for Reliable Computer Communication Protocols // ACM SIGCOMM Computer Communication Review : newsletter. — 1997. — Vol. 27, no. 2 (Апрель). — P. 24—36. — DOI:10.1145/263876.263881.
↑ Hamid Jafarkhani, Mahdi Hajiaghayi (22.10.2015). United States Patent Application Publication (PDF). COST-EFFICIENT REPAIR FOR STORAGE SYSTEMS USING PROGRESSIVE ENGAGEMENT. The Regents of the University of California,Oakland,CA (US). с. 1.
↑ ^а ^б ^в Dave K.Kythe, Prem K. Kythe. Algebraic and Stochastic Coding Theory. — 1-е изд. — CRC Press,, 2012. — С. 380—381. — ISBN 978-1439881811.

Література

Dave K. Kythe, Prem K. Kythe. Algebraic and Stochastic Coding Theory. — 1-е изд. — CRC Press, 2012. — С. 375—395. — ISBN 978-1439881811.

[:4-1] а ^б Шинкаренко К.В., Кориков A.M. Помехоустойчивое кодирование мультимедиа данных в компьютерных сетях // Известия Томского политехнического университета [Известия ТПУ] : журнал. — 2008. — Т. 313, № 5, Число 29 (сентябрь). — С. 37—41. — ISSN 1684-8519.

[2] Шинкаренко Константин Всеволодович, Кориков Анатолий Михайлович. Исследование эффективности помехоустойчивых кодов Лаби // Доклады Томского государственного университета систем управления и радиоэлектроники : журнал. — 2009. — 17 мая. — С. 185-192.

[:3-3] а ^б Katina Kralevska. Applied Erasure Coding in Networks and Distributed Storage // ResearchGate : thesis for the degree of Philosophiae Doctor. — 2018. — Март. — P. 7.

[parityCheck-4] а ^б J.S. Plank ; A.L. Buchsbaum ; R.L. Collins ; M.G. Thomason. Small parity-check erasure codes - exploration and observations // 2005 International Conference on Dependable Systems and Networks (DSN'05) : conference. — 2005. — . — Июль. — P. 2. — ISSN 1530-0889.

[:1-5] а ^б ^в ^г ^д Dave K. Kythe, Prem K. Kythe. Algebraic and Stochastic Coding Theory. — 1-е изд. — CRC Press, 2012. — С. 377—378. — ISBN 978-1439881811.

[6] Alexandros G. Dimakis, P. Brighten Godfrey, Martin J. Wainwright and Kannan Ramchandran. Network Coding for Distributed Storage Systems // IEEE Transactions on Information Theory : journal. — 2007. — Vol. 56, no. 9, (Август). — P. 4539—4551. — ISSN 0018-9448. — DOI:10.1109/TIT.2010.2054295.

[7] N. Alon ; J. Edmonds ; M. Luby. Linear time erasure codes with nearly optimal recovery // Proceedings of IEEE 36th Annual Foundations of Computer Science : symposium. — 1995. — . — Октябрь. — P. 1. — ISSN 0272-5428. — DOI:10.1109/SFCS.1995.492581.

[:0-8] а ^б Petar Maymounkov, David Mazi`eres. Rateless Codes And Big Downloads // 2nd International Workshop on Peer-to-Peer Systems : conference. — 2004. — Vol. 2735 (Август). — P. 2. — DOI:10.1007/978-3-540-45172-3_23.

[Luigi-9] Luigi Rizzo. Effective Erasure Codes for Reliable Computer Communication Protocols // ACM SIGCOMM Computer Communication Review : newsletter. — 1997. — Vol. 27, no. 2 (Апрель). — P. 24—36. — DOI:10.1145/263876.263881.

[10] Hamid Jafarkhani, Mahdi Hajiaghayi (22.10.2015). United States Patent Application Publication (PDF). COST-EFFICIENT REPAIR FOR STORAGE SYSTEMS USING PROGRESSIVE ENGAGEMENT. The Regents of the University of California,Oakland,CA (US). с. 1.

[:2-11] а ^б ^в Dave K.Kythe, Prem K. Kythe. Algebraic and Stochastic Coding Theory. — 1-е изд. — CRC Press,, 2012. — С. 380—381. — ISBN 978-1439881811.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

Надлишковий код: відмінності між версіями

Версія за 16:37, 31 січня 2022

Зміст

Принцип роботи