Ядрове згладжування

Ядрове згладжування або згладження (kernel smoother) — це статистичний метод оцінки дійснозначної функції $f:\mathbb {R} ^{p}\to \mathbb {R}$ як середньозважене значення сусідніх спостережених точок. Вага задається ядром, так щоб найближчі точки отримують найвищі ваги. Оцінювана функція є гладкою, а рівень гладкості задається єдиним параметром. Ядрове згладжування є типом зваженого рухомого середнього.

Означення

Нехай $K_{h_{\lambda }}(X_{0},X)$ ядро, задане формулою

$K_{h_{\lambda }}(X_{0},X)=D\left({\frac {\left\|X-X_{0}\right\|}{h_{\lambda }(X_{0})}}\right)$

де:

• $X,X_{0}\in \mathbb {R} ^{p}$
• $\left\|\cdot \right\|$ - евклідова норма
• $h_{\lambda }(X_{0})$ - параметр (радіус ядра)
• D ( t ) зазвичай позитивна дійсна функція, значення якої зменшується (або не зростає) зі збільшенням відстані між X і X₀ .

Популярні ядра, що використовуються для згладжування, включають параболічне (Епанечнікова), кубне та гауссове ядра.

Нехай $Y(X):\mathbb {R} ^{p}\to \mathbb {R}$ - неперервною функцією від X. Для кожного $X_{0}\in \mathbb {R} ^{p}$, ядро-зважене середнє Надарая-Ватсона (згладжена оцінка Y(X)) визначається

${\hat {Y}}(X_{0})={\frac {\sum \limits _{i=1}^{N}{K_{h_{\lambda }}(X_{0},X_{i})Y(X_{i})}}{\sum \limits _{i=1}^{N}{K_{h_{\lambda }}(X_{0},X_{i})}}}$

де:

• N – кількість спостережуваних точок
• Y ( X _i ) — спостереження в точках X_i .

Далі ми опишемо деякі окремі випадки ядрових згладжень.

Ядрове згладження Гауса

Ядро Гауса є одним із найпоширеніших ядер і виражається за допомогою рівняння

$K(x^{*},x_{i})=\exp \left(-{\frac {(x^{*}-x_{i})^{2}}{2b^{2}}}\right)$

Тут b — масштаб довжини для вхідного простору.

Ядрове згладження найближчих точок

Ідея ядрового згладження найближчого сусіда полягає в наступному. Для кожної точки X₀ беремо m найближчих сусідів і оцінюємо значення Y(X₀) шляхом усереднення значень цих сусідів.

Формально, $h_{m}(X_{0})=\left\|X_{0}-X_{[m]}\right\|$, де $X_{[m]}$ є m-м найближчим до X₀ сусідом, і

$D(t)={\begin{cases}1/m&{\text{if }}|t|\leq 1\\0&{\text{otherwise}}\end{cases}}$

Наприклад:

У цьому прикладі X є одновимірним. Для кожного X₀, ${\hat {Y}}(X_{0})$ є середнім значенням 16 найближчих до X₀ точок (позначено червоним кольором). Результат недостатньо гладкий.

Середньо ядрове згладження

Ідея середньо ядрового згладження полягає в наступному. Для кожної точки даних X₀ виберемо стале значення відстані λ (радіус ядра або ширину вікна для p = 1 вимір) і обчислимо зважене середнє для всіх точок даних, які ближче ніж $\lambda$ до X₀ (чим ближче до X₀ точки тим більшу вагу вони отримають).

Формально, $h_{\lambda }(X_{0})=\lambda ={\text{constant}},$ а D(t) — одне з популярних ядер.

Наприклад:

Для кожного X₀ ширина вікна стала, а вага кожної точки у вікні схематично позначена жовтою тінню на графіку. Видно, що оцінка плавна, але граничні точки зміщені. Причиною цього є неоднакова кількість точок (справа і зліва до X₀ ) у вікні, коли X₀ знаходиться досить близько до межі.

Локальна лінійна регресія

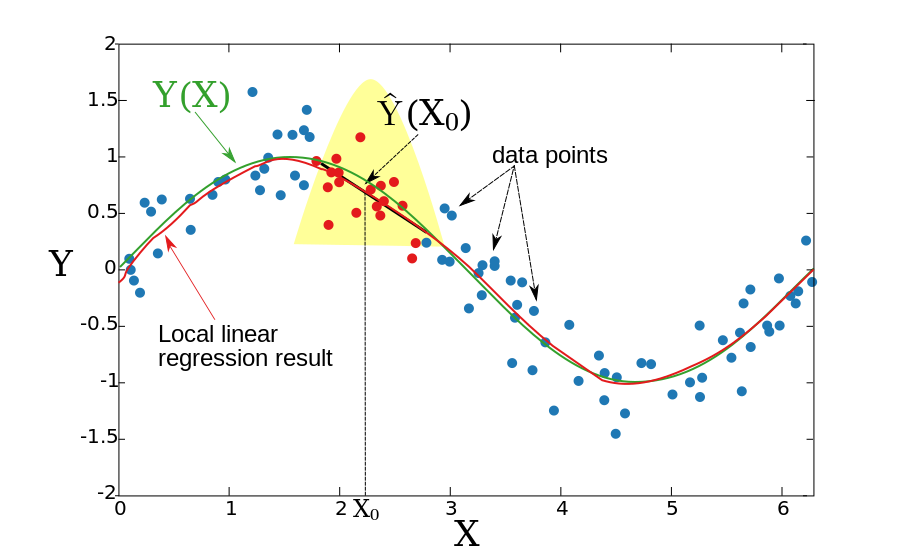
У двох попередніх розділах закладалось, що базова функція Y(X) локально константа, що давало змогу використовувати середньозважене значення оцінки. Ідея локальної лінійної регресії полягає в тому, що функція локально відповідає прямій лінії (чи гіперплощині у випадку вищих порядків), а не константі (горизонтальній лінії). Після підгонки лінії оцінка ${\hat {Y}}(X_{0})$ визначається значенням цієї лінії в точці X₀. Повторюючи цю процедуру для кожного X₀, можна отримати оцінку-функцію ${\hat {Y}}(X)$. Як і в розділі вище ширина вікна постійна $h_{\lambda }(X_{0})=\lambda ={\text{constant}}.$ Формально локальна лінійна регресія обчислюється шляхом оптимізації зваженої задачі найменшого квадрата.

У одновимірному випадку ( p = 1):

${\begin{aligned}&\min _{\alpha (X_{0}),\beta (X_{0})}\sum \limits _{i=1}^{N}{K_{h_{\lambda }}(X_{0},X_{i})\left(Y(X_{i})-\alpha (X_{0})-\beta (X_{0})X_{i}\right)^{2}}\\&\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\Downarrow \\&\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\hat {Y}}(X_{0})=\alpha (X_{0})+\beta (X_{0})X_{0}\\\end{aligned}}$

Розв'язок у вигляді формули:

${\hat {Y}}(X_{0})=\left(1,X_{0}\right)\left(B^{T}W(X_{0})B\right)^{-1}B^{T}W(X_{0})y$

де:

• $y=\left(Y(X_{1}),\dots ,Y(X_{N})\right)^{T}$
• $W(X_{0})=\operatorname {diag} \left(K_{h_{\lambda }}(X_{0},X_{i})\right)_{N\times N}$
• $B^{T}=\left({\begin{matrix}1&1&\dots &1\\X_{1}&X_{2}&\dots &X_{N}\\\end{matrix}}\right)$

Наприклад:

Отримана функція є гладкою, і проблема зі зміщеними граничними точками не настільки кричуща.

Локальну лінійну регресію можна застосувати у будь-якому просторі, хоча питання про те, що таке локальне сусідство ускладнюється. Зазвичай використовують k найближчих тренувальних точок до тестової точки, щоб відповідати локальній лінійній регресії. Це може призвести до великої дисперсії встановленої функції. Щоб обмежити дисперсію, набір навчальних точок повинен містити тестову точку у своїй опуклій оболонці (див. посилання на Gupta et al.).

Локальна поліноміальна регресія

Замість підгонки локально лінійних функцій можна допасувати поліноміальні функції.

Для p=1 слід розв'язати задачу мінімізації:

${\underset {\alpha (X_{0}),\beta _{j}(X_{0}),j=1,...,d}{\mathop {\min } }}\,\sum \limits _{i=1}^{N}{K_{h_{\lambda }}(X_{0},X_{i})\left(Y(X_{i})-\alpha (X_{0})-\sum \limits _{j=1}^{d}{\beta _{j}(X_{0})X_{i}^{j}}\right)^{2}}$

з ${\hat {Y}}(X_{0})=\alpha (X_{0})+\sum \limits _{j=1}^{d}{\beta _{j}(X_{0})X_{0}^{j}}$

У загальному випадку (p>1) слід мінімізувати:

${\begin{aligned}&{\hat {\beta }}(X_{0})={\underset {\beta (X_{0})}{\mathop {\arg \min } }}\,\sum \limits _{i=1}^{N}{K_{h_{\lambda }}(X_{0},X_{i})\left(Y(X_{i})-b(X_{i})^{T}\beta (X_{0})\right)}^{2}\\&b(X)=\left({\begin{matrix}1,&X_{1},&X_{2},...&X_{1}^{2},&X_{2}^{2},...&X_{1}X_{2}\,\,\,...\\\end{matrix}}\right)\\&{\hat {Y}}(X_{0})=b(X_{0})^{T}{\hat {\beta }}(X_{0})\\\end{aligned}}$

Див. також

• Фільтр Савицького–Голея
• Методи ядра
• Оцінка щільності ядра
• Локальна регресія
• Ядерна регресія

Список літератури

• Li, Q. and J.S. Racine. Nonparametric Econometrics: Theory and Practice. Princeton University Press, 2007, ISBN 0-691-12161-3.
• T. Hastie, R. Tibshirani and J. Friedman, The Elements of Statistical Learning, Chapter 6, Springer, 2001. ISBN 0-387-95284-5ISBN 0-387-95284-5 (companion book site).
• M. Gupta, E. Garcia and E. Chin, "Adaptive Local Linear Regression with Application to Printer Color Management," IEEE Trans. Image Processing 2008.