Статистика
| Статистика |
|---|
 |

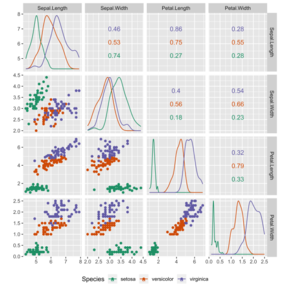
Стати́стика (англ. statistics) — це дисципліна, що працює над збиранням, організуванням, аналізом, інтерпретуванням та представленням даних.[1][2][3][4] В застосуванні статистики до наукової, промислової або соціальної задачі є звичним починати з генеральної сукупності (англ. statistical population) або статистичної моделі для дослідження. Генеральні сукупності можуть бути різноманітними групами людей або об'єктів, такими як «всі люди, що живуть в якійсь країні» або «кожен з атомів, що складають кристал». Статистика працює зі всіма аспектами даних, включно з плануванням збирання даних в термінах планування обстежень (англ. surveys) та експериментів.[5] Див. глосарій теорії ймовірностей та статистики[en].
Коли зібрати дані перепису (англ. census) неможливо, статистики збирають дані, розробляючи спеціальні плани експериментів (англ. experiment designs), та вибірки (англ. samples) для обстежування. Репрезентативне вибирання забезпечує можливість розумного розширення висновків та рішень з цієї вибірки на сукупність в цілому. Експериментальне дослідження (англ. experimental study) включає здійснення вимірювань досліджуваної системи, маніпулювання цією системою, а потім здійснення додаткових вимірювань із застосуванням тієї ж процедури, щоби визначити, чи змінило маніпулювання значення цих вимірювань. На противагу цьому, спостережне дослідження[en] (англ. observational study) не включає експериментального маніпулювання.
В аналізі даних використовують два основні статистичні методи: описову статистику (англ. descriptive statistics), яка узагальнює дані з вибірки із застосуванням статистичних індексів[en], таких як середнє значення та стандартне відхилення, та індуктивну статистику (англ. inferential statistics), яка робить висновки з даних, що піддаються випадковій мінливості (наприклад, похибкам спостережень, варіюванню вибірки).[6][7] Описова статистика часто найбільше цікавиться двома наборами властивостей розподілу (вибірки або загальної сукупності): центральна тенденція (або положення) прагне схарактеризувати центральне або типове значення цього розподілу, тоді як дисперсія (або мінливість) характеризує міру, до якої члени цього розподілу відхиляються від його центру, та один від одного. Висновування в математичній статистиці здійснюють в рамках теорії ймовірностей, що займається аналізом випадкових явищ.
Стандартна статистична процедура включає збирання даних, що веде до перевірки взаємозв'язку між двома наборами статистичних даних, або набором даних та синтетичними даними, отриманими з ідеалізованої моделі. Для статистичного взаємозв'язку між двома наборами даних пропонують гіпотезу, і порівнюють її, як альтернативу[en], з ідеалізованою нульовою гіпотезою (англ. null hypothesis) про відсутність взаємозв'язку між цими двома наборами даних. Відхиляння або спростування нульової гіпотези здійснюють із застосуванням статистичних критеріїв (англ. statistical tests), що кількісно виражають сенс, в якому хибність нульової гіпотези можливо вважати доведеною за наданих даних, які використовують в цій перевірці. Працюючи від нульової гіпотези, розпізнаю́ть два основні види помилок: помилки I роду (нульову гіпотезу хибно відхиляють, що дає «хибно позитивне», англ. false positive), та помилки II роду (нульову гіпотезу не вдається відхилити, й справжній взаємозв'язок між сукупностями втрачається, що дає «хибно негативне», англ. false negative).[8] З цією системою виявилося пов'язано численні проблеми: від отримування достатнього розміру вибірки, й до вказування адекватної нульової гіпотези.[джерело?]
Процеси вимірювання, що породжують статистичні дані, також піддаються помилкам. Багато з цих помилок класифікують як випадкові (шум, англ. noise) або систематичні (упередження, англ. bias), але можуть траплятися й інші типи помилок (наприклад, промахи, англ. blunder, такі як коли аналітик повідомляє неправильні одиниці вимірювання). Існування пропущених даних[en] або цензурування[en] може призводити до упереджених оцінок, й для подолання цих проблем було розроблено спеціальні методики.
Найраніші праці з імовірності та статистики, статистичних методів, що спираються на теорію ймовірностей, сходять до арабських математиків та криптографів[en], зокрема, Аль-Халіля (717—786)[9] та Аль-Кінді (801—873).[10][11] У XVIII сторіччі статистика також почала сильно живитися з диференціального та інтегрального числення. Останніми роками для вироблення цих критеріїв, таких як описовий аналіз, статистика покладалася більше на статистичне програмне забезпечення.[12]
Вступ[ред. | ред. код]
| Частина серії статей з статистики |
| Теорія ймовірностей |
|---|
 |
Статистика — це математичний масив наукових знань, що стосуються збирання, аналізу, інтерпретування або пояснювання, та представлення даних,[13][4] або одна з галузей математики.[14] Дехто вважає статистику радше окремою математичною наукою, ніж галуззю математики. В той час як даними користуються багато наукових досліджень, статистика займається використанням даних в контексті невизначеності, та ухвалюванням рішень в умовах невизначеності.[15][16]
В застосуванні статистики до задачі звичною практикою є починати з сукупності або процесу для дослідження. Сукупності можуть бути різноманітної тематики, такі як «всі люди, що мешкають у країні» або «кожен з атомів, що складають кристал». В ідеалі статистики збирають дані про всю сукупність (операція, звана переписом). Це може бути зорганізовано державними статистичними установами. Описову статистику можливо використовувати для узагальнювання даних про сукупність. До чисельних описувачів для неперервних типів даних (таких, як дохід) належать середнє значення та стандартне відхилення, тоді як в термінах описування категорійних даних (таких, як освіта) кориснішими є частота та відсоток.
Коли перепис є нездійсненним, досліджують обрану підмножину сукупності, звану вибіркою (англ. sample). Щойно визначено вибірку, яка для цієї сукупності є репрезентативною, дані для членів цієї вибірки збирають у спостережній або експериментальній постановці. Знов-таки, для узагальнювання цих вибіркових даних можливо застосовувати описову статистику. Проте, вибирання вибірки мало елементи випадковості, тож встановлені чисельні описувачі з цієї вибірки залежать від випадковості. Щоби все ж таки робити змістовні висновки про сукупність в цілому, потрібна індуктивна статистика. Вона використовує закономірності в даних вибірки, щоби робити висновки про представлену нею сукупність, з урахуванням випадковості. Ці висновки можуть набувати вигляду: відповідання на питання «так/ні» (перевіряння гіпотез, англ. hypothesis testing), оцінювання чисельних характеристик даних (оцінювання, англ. estimation), описування пов'язаностей (англ. associations) в даних (кореляція), та моделювання взаємозв'язків всередині даних (наприклад, із застосуванням регресійного аналізу). Висновування може розширюватися до прогнозування, передбачування, та оцінювання неспостережуваних змінних чи то всередині досліджуваної сукупності, чи пов'язаних із нею; до нього можуть належати екстраполювання та інтерполювання часових рядів та просторових даних, а також добування даних.
Математична статистика[ред. | ред. код]
Математична статистика — це застосування математики до статистики. До математичних методик, які для цього використовують, належать математичний аналіз, лінійна алгебра, стохастичний аналіз, диференціальні рівняння та теорія ймовірностей теорії міри[en].[17][18]
Історія[ред. | ред. код]

Детальніші відомості з цієї теми ви можете знайти в статті Історія статистики[en] та Засновники статистики[en].
Найраніші праці з імовірності та статистики сходять до арабських математиків та криптографів[en] Золотої доби ісламу між VIII та XIII сторіччями. Аль-Халіль (717—786) написав «Книгу таємної мови», що містить перше застосування перестановок та комбінацій[en] з метою перелічування всіх арабських слів з голосними та без них.[9] Найранішою книгою зі статистики є «Трактат про дешифрування криптографічних повідомлень», написаний арабським вченим Аль-Кінді (801—873). У своїй книзі Аль-Кінді навів докладний опис того, як застосовувати статистику та частотний аналіз для розшифровування зашифрованих повідомлень. Цей текст заклав основи статистики та криптоаналізу.[10][11] Аль-Кінді також здійснив найраніше з відомих застосування статистичного висновування, тоді як пізніші арабські криптографи розробили ранні статистичні методи для розкодовування зашифрованих повідомлень. Ібн Адлан[en] (1187—1268) пізніше зробив важливий внесок стосовно застосування в частотному аналізі розміру вибірки.[9]
Найраніші європейські праці зі статистики сходять до 1663 року, публікації «Природні та політичні спостереження на списках померлих» Джона Ґраунта.[19] Ранні застосування статистичного мислення оберталися довкола потреб держав (лат. statum) ґрунтувати політику на демографічних та економічних даних, звідси етимологія «стат-»[en]. На початку XIX сторіччя сфера дисципліни статистики розширилася, включивши збирання та аналіз даних в цілому. Натепер статистику широко застосовують в урядуванні, бізнесі, а також природничих та соціальних науках.
Математичні основи сучасної статистики було закладено в XVII сторіччі з розробкою Джироламо Карданом, Блезом Паскалем та П'єром Ферма теорії ймовірностей. Математична теорія ймовірностей постала з досліджень ігор випадку, хоч поняття ймовірності й було вже досліджено в середньовічному праві, та філософами, такими як Хуан Карамуель.[20] Метод найменших квадратів було вперше описано Адрієном-Марі Лежандром 1805 року.

Сучасна галузь статистики виникла наприкінці XIX — початку XX сторіччя в три етапи.[21] Першу хвилю, на рубежі сторіч, очолила праця Френсіса Ґолтена та Карла Пірсона, які перетворили статистику на строгу математичну дисципліну, яку використовували для аналізу, і не лише в науці, але також і в промисловості та політиці. До внеску Ґолтена належать введення понять стандартного відхилення, кореляції, регресійного аналізу, та застосування цих методів до дослідження розмаїття людських характеристик — зросту, ваги, довжини вій тощо.[22] Пірсон, серед іншого, розробив коефіцієнт кореляції моменту добутку Пірсона, визначений як момент добутку,[23] метод моментів для допасовування розподілів до вибірок, та розподіл Пірсона[en].[24] Ґолтен та Пірсон заснували «Biometrika[en]» як перший журнал з математичної статистики та біостатистики (яку тоді називали біометрією), й пізніше заснували перший в світі університетський статистичний факультет в Університетськім коледжі Лондона.[25]
Рональд Фішер під час експерименту «пані дегустує чай» закарбував термін нульова гіпотеза, яку «ніколи не доводять та не встановлюють, але, можливо, спростовують в ході експерименту».[26][27]
Початок другій хвилі 1910-х та 20-х років поклав Вільям Сілі Ґоссет[en], й вона досягла своєї кульмінації в осяяннях Рональда Фішера, який написав підручники, що мали визначити цю академічну дисципліну в університетах по всьому світі. Найважливішими публікаціями Фішера були його засаднича праця 1918 року «Кореляція між родичами в припущенні менделевої спадковості[en]» (яка була першою, де було застосовано статистичний термін «дисперсія», англ. variance), його класична праця 1925 року «Статистичні методи для дослідників[en]», та його «Планування експериментів[en]» 1935 року,[28][29][30] де він розробив строгі моделі планування експериментів. Він започаткував поняття достатності, допоміжної статистики[en], лінійного розрізнювача Фішера та інформації за Фішером.[31] У своїй книзі 1930 року «Генетична теорія природного добору[en]» він застосував статистику до різних біологічних понять, таких як принцип Фішера[32] (що його Е. В. Ф. Едвардс[en] назвав «імовірно найвизначнішим аргументом в еволюційній біології») та фішерова неконтрольованість,[33][34][35][36][37][38] поняття в статевім доборі про афект неконтрольованого зворотного зв'язку, що виникає в еволюції.
Заключна хвиля, яка переважно бачила вдосконалення та розширення попередніх розробок, виникла в результаті спільної праці Еґона Пірсона та Єжи Неймана в 1930-х роках. Вони ввели поняття помилки «II роду», статистичної потужності критерію (англ. power of a test), та довірчих інтервалів. Єжи Нейман 1934 року показав, що стратифіковане випадкове вибирання було в цілому кращим методом оцінювання, аніж вибирання цілеспрямоване (квотне).[39]
Сьогодні статистичні методи застосовують в усіх областях, які передбачають ухвалювання рішень, щоби отримувати точні висновки з консолідованого масиву даних для ухвалювання рішень в умовах невизначеності на основі статистичної методології. Використання сучасних комп'ютерів форсувало великомасштабні статистичні обчислення й також уможливило нові методи, що є недоцільними для виконання вручну. Статистика продовжує бути областю активних досліджень, наприклад, щодо проблеми аналізу великих даних.[40]
Статистичні дані[ред. | ред. код]
Збирання даних[ред. | ред. код]
Вибирання[ред. | ред. код]
Коли зібрати дані повного перепису неможливо, статистики збирають вибіркові дані, розробляючи особливі плани експериментів та вибірки для обстеження[en]. Статистика сама по собі також пропонує інструменти для передбачування та прогнозування за допомогою статистичних моделей. Ідея робити висновки на основі вибіркових даних виникла близько середини 1600-х у зв'язку з оцінюванням чисельності населення та розробки предтеч страхування життя.[41]
Щоби використовувати вибірку як взірець для всієї сукупності, важливо, щоби вона справді представляла генеральну сукупність. Репрезентативне вибирання забезпечує можливість безпечного розширення висновків та рішень з цієї вибірки на сукупність в цілому. Основна проблема полягає у визначені міри, до якої обрана вибірка є насправді репрезентативною. Статистика пропонує методи для оцінювання та виправляння будь-яких упереджень у вибірці та процедурах збирання даних. Також існують методи планування експериментів для таких експериментів, що можуть зменшувати ці проблеми на початку дослідження, підсилюючи його здатність розпізнавати істину стосовно генеральної сукупності.
Теорія вибирання є частиною математичної дисципліни теорії ймовірності. Ймовірність використовують в математичній статистиці, щоби досліджувати вибіркові розподіли вибіркових статистик та, загальніше, властивості статистичних процедур. Використання будь-якого статистичного методу є правильним, коли система або сукупність, яку розглядають, задовольняє припущення цього методу. Різниця в поглядах класичної теорії ймовірності та теорії вибирання, грубо, полягає в тім, що теорія ймовірності починає з заданих параметрів генеральної сукупності для дедуктивного виведення ймовірностей, притаманних вибіркам. Проте статистичне висновування рухається в протилежному напрямку, індуктивно виводячи з вибірок параметри більшої або генеральної сукупності.
Експериментальні та спостережні дослідження[ред. | ред. код]
Загальною метою статистичного дослідницького проєкту є дослідження причинності, й зокрема висновування стосовно впливу змін значень передбачувачів чи незалежних змінних на залежні змінні. Існує два основні типи причиннісних статистичних досліджень: експериментальні дослідження, та спостережні дослідження[en]. В обох типах досліджень спостерігають за впливом відмінності в незалежній змінній (або змінних) на поведінку залежної змінної. Різниця між цими двома типами полягає в тім, як фактично здійснюють дослідження. Кожен з них може бути дуже дієвим. Експериментальне дослідження включає вимірювання досліджуваної системи, маніпулювання цією системою, а потім здійснення нових вимірювань з використанням тієї ж процедури, щоби визначити, чи змінило це маніпулювання значення вимірювань. На противагу цьому, спостережне дослідження не містить експериментального маніпулювання. Натомість збирають дані та досліджують кореляції між передбачувачами та відгуками. Й хоч інструменти аналізу даних найкраще працюють на даних з рандомізованих досліджень, їх також застосовують і до інших типів даних, таких як природні експерименти та спостережні дослідження[en],[42] для яких статистик використовуватиме видозмінений, структурованіший метод оцінювання (наприклад, серед багатьох інших, оцінювання різниці в різницях[en] та інструментальні змінні), що вироблятиме слушні оцінювачі.
Експерименти[ред. | ред. код]
Основними етапами статистичного експерименту є:
- Планування дослідження, включно зі знаходженням числа повторювань дослідження, із застосуванням наступної інформації: попередніх оцінок стосовно розміру ефекту впливу[en], альтернативних гіпотез[en], та оцінюваної експериментальної мінливості. Необхідним є розгляд вибору об'єктів експерименту та етики дослідження. Статистики радять, щоб експерименти порівнювали (щонайменше) один новий вплив зі стандартним впливом або керуванням, щоби уможливити неупереджену оцінку відмінності ефектів впливу.
- Планування експериментів, із застосуванням групування, щоби знижувати вплив змішувальних змінних, та увипадковлених призначень[en] впливів до об'єктів, щоби уможливлювати неупереджені оцінки ефектів впливів та експериментальної похибки. На цьому етапі експериментатори та статистики пишуть протокол експерименту (англ. experimental protocol), що керуватиме виконанням експерименту, й що визначатиме первинний аналіз (англ. primary analysis) експериментальних даних.
- Виконання експерименту згідно протоколу експерименту та аналізування даних згідно протоколу експерименту.
- Подальше вивчення набору даних у вторинних аналізах з метою висування нових гіпотез для майбутнього вивчення.
- Документування та представлення результатів дослідження.
Експерименти з людською поведінкою несуть особливі турботи. В знаменитім Готорнськім дослідженні вивчали зміни до робочого середовища на Готорнськім заводі компанії Western Electric. Дослідників цікавило визначити, чи призведе збільшення освітлення до збільшення продуктивності працівників конвеєра[en]. Дослідники спочатку виміряли продуктивність заводу, потім змінили освітлення в одній області заводу, й перевірили, чи вплинули ці зміни в освітленні на продуктивність. Виявилося, що продуктивність і справді покращилася (в експериментальних умовах). Проте це дослідження сьогодні сильно критикують через помилки в процедурах експерименту, особливо через брак контрольної групи та сліпоти. Готорнський ефект стосується виявлення того, що результат (в цьому випадку — продуктивність працівників) змінився через саме спостереження. Піддослідні в Готорнськім дослідженні стали продуктивнішими не через зміну освітлення, а через те, що за ними спостерігали.[43]
Спостережне дослідження[ред. | ред. код]
Прикладом спостережного дослідження є таке, що вивчає пов'язаність паління та раку легенів. Цей тип дослідження зазвичай використовує опитування для збирання спостережень про цільову область, і потім виконує статистичний аналіз. В цьому випадку дослідники збирали би спостереження як про курців, так і про не курців, певно, шляхом когортного дослідження, а потім дивилися би на число випадків раку легенів у кожній з груп.[44] Іншим типом спостережного дослідження є дослідження «випадок—контроль», в якому запрошують взяти участь людей з та без цільового результату (наприклад, раку легенів), і збирають їхні історії піддавання впливові.
Типи даних[ред. | ред. код]
Детальніші відомості з цієї теми ви можете знайти в статті Типи статистичних даних[en] та Шкала.
Існувало чимало спроб виробити таксономію шкал вимірювання. Психолог Стенлі Сміт Стівенс[en] визначив номінальну (англ. nominal), порядкову (англ. ordinal), інтервальну (англ. interval) шкали, та шкалу відношень (англ. ratio scale). Номінальні вимірювання не мають змістовного порядку ранжування їхніх значень, й дозволяють будь-яке перетворення один-в-одного (ін'єктивне). Порядкові вимірювання мають неточні відмінності між послідовними значеннями, але мають змістовний порядок цих значень, й дозволяють будь-яке перетворення зі збереженням порядку. Інтервальні вимірювання мають визначені змістовні відстані між вимірюваннями, але нульове значення є довільним (як у випадках вимірювань довготи та температури в градусах Цельсія та Фаренгейта), й дозволяють будь-яке лінійне перетворення. Вимірювання відношень мають визначені змістовні як нульове значення, так і відстані між вимірюваннями, й дозволяють будь-яке перетворення масштабування.
Оскільки змінні, що відповідають лише номінальним та порядковим вимірюванням, раціонально виміряти числами неможливо, іноді їх об'єднують як категорійні змінні, тоді як відносні та інтервальні вимірювання об'єднують як кількісні змінні, що можуть бути або дискретними, або неперервними, в силу своєї числової природи. Таке розмежування часто може бути нестрого співвідносним з типом даних в інформатиці, оскільки дихотомні категорійні змінні може бути представлено логічним типом даних, багатозначні категорійні змінні — довільно призначуваними цілими числами в цілочисловім типі даних, а неперервні змінні — дійснозначним типом даних[en] із застосуванням обчислень з рухомою комою. Але відображення типів даних інформатики на типи статистичних даних залежить від того, яку категоризацію останніх втілюють.
Було запропоновано й інші категоризації. Наприклад, Мостеллер та Тьюкі (1997)[45] розрізнювали ступені (англ. grades), ранги (англ. ranks), зліченні дроби (англ. counted fractions), кількості (англ. counts), суми (англ. amounts) та баланси (англ. balances). Нелдер (1990)[46] описав неперервні кількості (англ. continuous counts), неперервні відношення (англ. continuous ratios), відношення кількостей (англ. count ratios), та категорійні види даних. Див. також Крісмана (1998),[47] ван ден Берґа (1991).[48]
Питання доречності чи недоречності застосування різних видів статистичних методів до даних, отриманих з різних видів процедур вимірювання, ускладнюється питаннями перетворювання змінних та точною інтерпретацією досліджуваних питань. «Взаємозв'язок між даними та тим, що вони описують, просто відображає той факт, що певні види статистичних висловлень можуть мати значення істинності, що не є інваріантними за деяких перетворень. Чи є доцільним розглядати певне перетворення, чи ні, залежить від питання, на яке намагаються відповісти.»[49]
Статистичні методи[ред. | ред. код]
Описова статистика[ред. | ред. код]
Описо́ві стати́стики (в сенсі злічуваного іменника[en] англ. descriptive statistic в однині) — це зведені статистики, які кількісно описують або узагальнюють ознаки сукупності інформації,[50] в той час як опис́ова стати́стика в сенсі незлічуваного іменника (англ. descriptive statistics) — це процес використання та аналізу цих статистик. Описова статистика відрізняється від висновувальної статистики[51] (англ. inferential statistics, або індуктивної статистики, англ. inductive statistics) тим, що описова статистика має на меті узагальнювання вибірки, а не використання цих даних, щоб дізнатися щось про генеральну сукупність, яку, як вважають, ця вибірка даних представляє.
Індуктивна статистика[ред. | ред. код]
Статисти́чне висно́вування (англ. statistical inference) — це процес використання аналізу даних для встановлення властивостей розподілу ймовірності, що лежить в їх основі.[52] Висновувальний статистичний аналіз робить висновки про властивості генеральної сукупності, наприклад, шляхом перевіряння гіпотез та отримування оцінок. Він виходить з припущення, що спостережувані дані є вибіркою з більшої сукупності. Індуктивну статистику можливо протиставляти описовій статистиці. Описова статистика цікавиться виключно властивостями спостережуваних даних, і не спирається на припущення, що ці дані походять із більшої сукупності.
Термінологія та теорія індуктивної статистики[ред. | ред. код]
Статистики, статистичні оцінки, та центральні величини[ред. | ред. код]
Розгляньмо незалежні однаково розподілені (н. о. р.) випадкові змінні із заданим розподілом ймовірності: стандартне статистичне висновування та теорія оцінювання визначає випадкову вибірку як випадковий вектор, заданий стовпчиковим вектором цих н. о. р. змінних.[53] Досліджувану генеральну сукупність описують розподілом ймовірності, що може мати невідомі параметри.
Статистика (англ. statistic) — це випадкова змінна, що є функцією випадкової вибірки, але не функцією невідомих параметрів. Розподіл імовірності цієї статистики, проте, невідомі параметри мати може.
Розгляньмо тепер функцію невідомого параметра: статистична оцінка (англ. estimator) — це статистика, яку використовують для оцінювання цієї функції. До широко вживаних статистичних оцінок належать вибіркове середнє, незміщена дисперсія вибірки та коваріація вибірки[en].
Випадкову змінну, що є функцією випадкової вибірки та невідомого параметру, але чий розподіл імовірності не залежить від невідомого параметру, називають центральною величиною[en] (англ. pivotal quantity, pivot). До широко вживаних центральних величин належать z-оцінка, статистика хі-квадрат та t-величина Стьюдента.
Серед двох оцінок заданого параметру ефективнішою вважають ту, що має нижчу середньоквадратичну похибку. Крім того, оцінку називають незміщеною (англ. unbiased), якщо її математичне сподівання дорівнює істинному значенню оцінюваного невідомого параметра, й асимптотично незміщеною, якщо її математичне сподівання збігається до границі істинного значення такого параметра.
До інших бажаних властивостей статистичних оцінок належать: рівномірно незміщені оцінки з мінімальною дисперсією[en] (англ. UMVUE), що мають найнижчу дисперсію для всіх можливих значень оцінюваного параметра (це зазвичай є легшою властивістю для перевірки, ніж ефективність), та слушні оцінки (англ. consistent estimators), що збігаються за ймовірністю до істинного значення такого параметра.
Це все ще залишає відкритим питання, як отримувати статистичні оцінки в заданій ситуації та виконувати обчислення, було запропоновано декілька методів: метод моментів, метод максимальної правдоподібності, метод найменших квадратів, та новіший метод оцінних рівнянь[en].
Нульова гіпотеза та альтернативна гіпотеза[ред. | ред. код]
Інтерпретування статистичної інформації часто може включати розробку нульової гіпотези (англ. null hypothesis), яка зазвичай (але не обов'язково) полягає у відсутності взаємозв'язку серед змінних, або що зміни з часом не відбуваються.[54][55]
Найкращою ілюстрацією для новачка є утруднення, з яким зіткнувся кримінальний процес в суді присяжних. Нульова гіпотеза, H0, стверджує, що відповідач є невинним, тоді як альтернативна гіпотеза, H1, стверджує, що відповідач є винним. Висувається звинувачення через підозру в винності. H0 (статус кво) протистоїть H1, й підтримується, поки H1 не стане підтримано доказами «поза розумним сумнівом». Проте «нездатність відхилити H0» в цьому випадку означає не невинність, а лише те, що докази були недостатніми для засудження. Тож присяжні не обов'язково приймають H0, їм не вдається відхилити H0. І хоч «довести» нульову гіпотезу неможливо, її можливо перевірити на те, наскільки вона є близькою до істини, через статистичну потужність, яка робить перевірку на помилки другого роду.
Те, що статистики називають альтернативною гіпотезою[en], — це просто гіпотеза, що суперечить нульовій гіпотезі.
Похибка[ред. | ред. код]
Працюючи від нульової гіпотези, розпізнаю́ть два основні види помилок:
- Помилки I роду (англ. type I errors), коли нульову гіпотезу хибно відхиляють, що дає «хибно позитивне» (англ. false positive)
- Помилки II роду (англ. type II errors), коли нульову гіпотезу не вдається відхилити, й справжня відмінність між сукупностями втрачається, що дає «хибно негативне» (англ. false negative)
Стандартне відхилення (англ. standard deviation) вказує на те, наскільки окремі спостереження в вибірці відрізняються від центрального значення, такого як середнє за вибіркою або середнє за генеральною сукупністю, тоді як стандартна похибка (англ. standard error) вказує на оцінку різниці між середніми за вибіркою та середнім за генеральною сукупністю.
Статистична похибка (англ. statistical error) — це величина, на яку спостереження відрізняються від їхнього математичного сподівання, залишок (англ. residual) — це величина, на яку спостереження відрізняються від значення, якого набуває статистична оцінка очікуваного значення на заданому зразкові (яку також називають передбаченням).
Середньоквадратичну похибку (англ. mean squared error) використовують для отримування ефективних оцінок, широко вживаного класу статистичних оцінок. Коренева середньоквадратична похибка[en] (англ. root mean square error) є просто квадратним коренем середньоквадратичної похибки.

Багато статистичних методів прагнуть мінімізувати залишкову суму квадратів[en] (англ. residual sum of squares), і їх називають методами найменших квадратів (англ. methods of least squares), на противагу до методів найменших модулів[en] (англ. least absolute deviations). Останні надають однакової ваги як маленьким, так і великим похибкам, тоді як перші надають великим похибкам більшої ваги. Також, залишкова сума квадратів є диференційовною, що забезпечує зручну властивість для виконання регресії. Найменші квадрати в застосуванні до лінійної регресії називають звичайним методом найменших квадратів[en] (англ. ordinary least squares method), а найменші квадрати в застосуванні до нелінійної регресії[en] називають нелінійним методом найменших квадратів[en] (англ. non-linear least squares). Також, в лінійній регресійній моделі недетерміновану частину моделі називають членом похибки (англ. error term), збуренням (англ. disturbance), або просто шумом (англ. noise). Як лінійну, так і нелінійну регресію розглядають у поліноміальнім методі найменших квадратів (англ. polynomial least squares), що також описує дисперсію в передбаченні залежної змінної (вісь y) як функцію від незалежної змінної (вісь x) та відхилень (похибок, шуму, збурення) відносно оцінюваної (допасовуваної) кривої.
Процеси вимірювання, що породжують статистичні дані, також є схильними до похибок. Багато з цих похибок класифікують як випадкові (англ. random, шум) та систематичні (англ. systematic, зсув), але важливими можуть бути й інші типи похибок (наприклад, промахи, такі як коли аналітик повідомляє неправильні одиниці вимірювання). Існування пропущених даних[en] або цензурування[en] може призводити до упереджених оцінок, й для подолання цих проблем було розроблено спеціальні методики.[56]
Інтервальне оцінювання[ред. | ред. код]
Детальніші відомості з цієї теми ви можете знайти в статті Інтервальне оцінювання[en].
Більшість досліджень вибирають лише частину генеральної сукупності, тож результати не представляють всю генеральну сукупність вповні. Будь-які оцінки, отримані з такої вибірки, лише наближують значення генеральної сукупності. Довірчі інтервали (англ. confidence intervals) дозволяють статистикам виражати те, наскільки близько вибіркова оцінка відповідає істинному значенню для всієї генеральної сукупності. Часто їх виражають як 95-відсоткові довірчі інтервали. Формально, 95 %-вий довірчий інтервал для значення є діапазоном, який, якщо вибирання та аналіз повторювати за таких же умов (отримуючи відмінний набір даних), включатиме істинне значення (генеральної сукупності) в 95 % всіх можливих випадків. Це не означає, що ймовірність перебування істинного значення в цьому довірчому інтервалі становить 95 %. З частотницької точки зору таке твердження не має сенсу, оскільки істинне значення не є випадковою змінною. Істинне значення або перебуває в даному інтервалі, або ні. Проте, істинним є те, що до того, як буде вибрано якісь дані, і за заданого плану побудови довірчого інтервалу, ймовірність того, що інтервал, який ще належить обчислити, покриватиме істинне значення, становить 95 %: в цей момент межі інтервалу є випадковими змінними, які ще належить проспостерігати. Одним із підходів, що видає інтервал, який можливо інтерпретувати як такий, що має задану ймовірність вміщування істинного значення, є застосування ймовірних інтервалів (англ. credible intervals) з баєсової статистики: цей підхід залежить від відмінного способу інтерпретування того, що мається на увазі під «імовірністю», а саме, баєсової ймовірності.
Довірчі інтервали, в принципі, можуть бути симетричними та асиметричними. Інтервал може бути асиметричним, бо він працює як нижня та верхня межі для параметру (лівобічний та правобічний інтервали), але він також може бути асиметричним, оскільки цей двобічний інтервал будують із порушенням симетрії навколо оцінки. Іноді межі асимптотичного інтервалу досягають асимптотично, й використовують їх для наближення істинних меж.
Значущість[ред. | ред. код]
Статистика рідко дає на аналізоване питання просту відповідь на кшталт Так/Ні. Інтерпретація часто зводиться до рівня статистичної значущості (англ. statistical significance), застосовуваного до чисел, і часто посилається на ймовірність значення, що точно відкидає нульову гіпотезу (яку іноді називають p-значенням).

Стандартним підходом[53] є перевіряти нульову гіпотезу відносно альтернативної гіпотези. Критична область є множиною значень оцінювача, які ведуть до спростування нульової гіпотези. Ймовірність помилки I роду є відтак ймовірністю того, що оцінювач лежить у критичній області за умови, що нульова гіпотеза є істинною (статистична значущість), а ймовірність помилки II роду є ймовірністю того, що оцінювач не належить до критичної області за умови, що істинною є альтернативна гіпотеза. Статистична потужність (англ. statistical power) критерію є ймовірністю того, що він належним чином відхиляє нульову гіпотезу, коли ця нульова гіпотеза є хибною.
Посилання на статистичну значущість не обов'язково означає, що загальний результат є значущим в термінах реального світу. Наприклад, у великому дослідженні лікарського засобу може бути показано, що цей медикамент має статистично значущий, але дуже маленький сприятливий ефект, такий, що він навряд чи може помітно допомагати пацієнтові.
І хоча в принципі прийнятний рівень статистичної значущості може бути предметом обговорення, p-значення є найменшим рівнем значущості, який дозволяє критерію відхиляти нульову гіпотезу. Цей критерій є логічно рівнозначним твердженню, що p-значення є ймовірністю спостерігання результату, щонайменше настільки ж екстремального, як і статистика критерію, за умови, що нульова гіпотеза є істинною. Таким чином, що меншим є p-значення, то нижчою є ймовірність трапляння помилки I роду.
Деякі проблеми, зазвичай пов'язувані з цією системою (див. критику перевірки статистичних гіпотез[en]):
- Відмінність, яка має високу статистичну значущість, може все одно не мати практичної значущості, але можливо належно формулювати критерії, щоби враховувати це. Одна з відповідей передбачає вихід за межі повідомляння лише рівня значущості, шляхом включання p-значення при звітуванні про відхилення чи прийняття гіпотези. Проте, p-значення не показує розміру[en] чи важливості спостережуваного ефекту, а також може створювати враження перебільшеної важливості незначних відмінностей у великих дослідженнях. Кращим і все поширенішим підходом є повідомляти довірчі інтервали. Незважаючи на те, що їх отримують із тих же обчислень, що й статистичні критерії гіпотез та p-значення, вони описують розмір як самого ефекту, так і невизначеності, що його оточує.
- Хиба транспонованого обумовлення, вона ж помилка прокурора: критика виникає через те, що цей підхід перевірки гіпотез змушує віддавати перевагу одній з гіпотез (нульовій), оскільки оцінюють ймовірність спостережуваного результату за умови нульової гіпотези, а не ймовірність нульової гіпотези за спостереженого результату. Альтернативу цьому підходові запропоновано баєсовим висновуванням, хоча воно вимагає встановлювання апріорної ймовірності.[57]
- Відхилення нульової гіпотези не доводить автоматично альтернативну гіпотезу.
- Як і все в індуктивній статистиці, вона покладається на розмір вибірки, й відтак за важких хвостів[en] p-значення може бути обчислювано сильно помилково.[прояснити]
Приклади[ред. | ред. код]
Деякі відомі статистичні критерії та процедури:
- Дисперсійний аналіз (англ. ANOVA)
- Критерій хі-квадрат
- Кореляція
- Факторний аналіз
- U Манна—Уітні
- Зважене середньоквадратичне відхилення[en] (англ. MSWD)
- Коефіцієнт кореляції моменту добутку Пірсона
- Регресійний аналіз
- Коефіцієнт кореляції рангу Спірмена
- t-критерій Стьюдента
- Аналіз часових рядів
- Спільний аналіз[en][58]
Розвідувальний аналіз даних[ред. | ред. код]
Розві́дувальний ана́ліз да́них (РАД, англ. exploratory data analysis, EDA) — це один з підходів до аналізу наборів даних для узагальнювання їхніх основних характеристик, часто за допомогою візуальних методів. Статистичну модель можуть використовувати чи ні, але в першу чергу РАД призначено, щоби побачити, що дані можуть сказати нам за межами формальної задачі моделювання та перевірки гіпотез.
Неналежне застосування[ред. | ред. код]
Детальніші відомості з цієї теми ви можете знайти в статті Неналежне застосування статистики.
Неналежне застосування статистики може спричинювати тонкі, але серйозні помилки в описі та інтерпретації — тонкі в тому сенсі, що навіть досвідчені фахівці можуть робити такі помилки, а серйозні в тому сенсі, що вони можуть призводити до руйнівних помилок в ухвалюванні рішень. Від належного застосування статистики залежать, наприклад, соціальна політика, медична практика та надійність таких споруд, як мости.
Навіть коли статистичні методики застосовують коректно, їхні результати можуть бути складними для інтерпретування для тих, кому бракує досвіду. Статистична значущість тенденції в даних, яка вимірює ступінь, до якого тенденцію може бути спричинено випадковою мінливістю вибірки, може узгоджуватися з інтуїтивним відчуттям її значущості, а може й не узгоджуватися. Набір базових статистичних навичок (та скептицизму), необхідних людям для належної роботи з інформацією у своєму повсякденному житті, називають статистичною грамотністю[en].
Існує думка, що статистичні знання занадто часто цілеспрямовано застосовують неналежним чином, шукаючи шляхи інтерпретувати лише ті дані, що є сприятливими для доповідача.[59] Недовіра та нерозуміння статистики пов'язані з цитатою «Існує три види брехні: брехня, нахабна брехня й статистика». Неналежне застосування статистики може бути як ненавмисним, так і навмисним, й ряд міркувань окреслено в книзі «Як брехати за допомогою статистики».[59] В намаганні пролити світло на належне та неналежне застосування статистики проводять перегляди статистичних методик, використовуваних в певних областях (наприклад, Варн, Лазо, Рамос і Ріттер (2012)).[60]
До способів запобігання неналежному застосуванню статистики належать застосування правильних діаграм та запобігання упередженню.[61] Неналежне застосування може траплятися, коли висновки переузагальнюють, і претендують, що вони є репрезентативними для більшого, ніж вони є насправді, часто через навмисне або ненавмисне не враховування упередженості вибірки.[62] Стовпчикові діаграми є, мабуть, найпростішими діаграмами для застосування та розуміння, й їх можливо робити вручну або за допомогою простих комп'ютерних програм.[61] На жаль, більшість людей не дивляться на упередження та помилки, тож вони лишаються непоміченими. Таким чином, люди можуть часто вірити в те, що щось є істинним, навіть якщо воно не є достатньо репрезентативним.[62] Щоби зібрані зі статистики дані були правдоподібними та точними, здійснювана вибірка мусить бути репрезентативною для генеральної сукупності в цілому.[63] Згідно Гаффа, «Надійність вибірки може бути зруйновано [упередженістю]… дозволяйте собі певну міру скептицизму.»[64]
Для допомоги в розумінні статистики Гафф запропонував ряд питань, які слід задавати в кожному випадку:[59]
- Хто так каже? (Чи має він/вона корисливу мету?)
- Звідки він/вона знає? (Чи має він/вона ресурси, щоби знати ці факти?)
- Що упущено? (Чи надали він/вона повну картину?)
- Чи не змінив хтось тему? (Чи пропонують нам він/вона правильну відповідь на не ту задачу?)
- Чи має це сенс? (Чи є його/її висновок логічним та узгодженим з тим, що ми вже знаємо?)
Стентон Ґлентц[en], американський професор медицини, який викладає статистику студентам медичного профілю, автор ряду курсів та книг зі статистики та колишній редактор «Journal of the American College of Cardiology[en]», зазначає, що близько 50 % публікацій, які надходять в редакцію журналу, містять статистичні помилки отримання та обробки медичних даних.[65] Основними причинами є недостовірність отриманих даних (неправильно поставлені експерименти або ж взяті непрезентабельні дані), а також незнання та неправильне застосування статистичних методів. Також він зазначає, що часто дослідник та особи, причетні до експерименту, можуть підсвідомо видавати бажане за дійсне. Причому ненавмисне підтасування даних може відбуватися як на етапі постановки експерименту, збору даних, так і на етапі аналізу даних. Виходом є максимальне врахування та усунення сторонніх чинників, які можуть вплинути на процес експерименту та на аналіз даних. Він пропонує якомога ширше використовувати «сліпий метод» чи навіть «подвійно сліпий метод», коли ані піддослідні, ані дослідники (чи помічники дослідників) достеменно не знають, що на якій групі хворих досліджується, і навіть аналіз даних бажано щоб робила особа, незацікавлена у некоректній інтерпретації даних, чи, ще краще, якщо вона буде необізнаною в конкретних деталях експерименту. В будь-якому разі, в постановці, зборі та аналізі даних повинні брати участь особи, які добре володіють прикладними статистичними методами.
Неналежна інтерпретація: кореляція[ред. | ред. код]
Поняття кореляції особливо привертає увагу потенційною плутаниною, яку воно може спричинювати. Статистичний аналіз набору даних часто виявляє, що дві змінні (властивості) досліджуваної генеральної сукупності мають схильність змінюватися разом, так, ніби вони пов'язані. Наприклад, дослідження річного доходу, яке також дивиться на вік смерті, може виявити, що тривалість життя в бідних людей схильна бути меншою, ніж у заможних. Про ці дві змінні кажуть, що вони корелюють, проте, вони можуть бути, а можуть і не бути причиною одна одної. Явище кореляції може бути спричинено третім, раніше не розгляданим явищем, що називають неявною змінною (англ. lurking variable) або змішувальною змінною (англ. confounding variable). З цієї причини немає можливості негайно зробити висновок про існування причинно-наслідкового зв'язку між цими двома змінними. (Див. корелювання не означає спричинювання.)
Застосування[ред. | ред. код]
Прикладна статистика, теоретична статистика та математична статистика[ред. | ред. код]
Прикладна статистика включає описову статистику та застосування індуктивної статистики.[66][67] Теоретична статистика розглядає логічні аргументи, що лежать в основі обґрунтування підходів до статистичного висновування, а також охоплює математичну статистику. Математична статистика включає не лише маніпулювання розподілами ймовірності, необхідними, щоби виводити результати, пов'язані з методами оцінювання та висновування, але також і різні аспекти обчислювальної статистики[en] та планування експериментів.
Статистичні консультанти[en] можуть допомагати організаціям та компаніям, які не мають власної компетенції, що стосується їхніх конкретних питань.
Машинне навчання та добування даних[ред. | ред. код]
Моделі машинного навчання — це статистичні та ймовірнісні моделі, що фіксують закономірності в даних через застосування обчислювальних алгоритмів.
Статистика в академічнім середовищі[ред. | ред. код]
Статистику застосовують до широкого спектру академічних дисциплін, включно з природничими та суспільними науками, урядуванням та бізнесом. Бізнесова статистика застосовує статистичні методи в економетрії, аудиті, виробництві та операційній діяльності, включно з удосконаленням обслуговування та маркетинговими дослідженнями.[68] В галузі біологічних наук 12-ма найчастішими статистичними критеріями є: дисперсійний аналіз (англ. ANOVA), критерій хі-квадрат, t-критерій Стьюдента, лінійна регресія, коефіцієнт кореляції Пірсона, U-критерій Манна — Уітні, критерій Краскела — Уоліса[en], індекс різноманітності Шеннона, критерій Тьюкі[en], кластерний аналіз, коефіцієнт кореляції рангу Спірмена та метод головних компонент.[69]
Типовий курс статистики охоплює описову статистику, ймовірність, біноміальний та нормальний розподіли, перевірку гіпотез та довірчих інтервалів, лінійну регресію та кореляцію.[70] Сучасні фундаментальні курси статистики для студентів останнього курсу зосереджуються на правильному обиранні критеріїв, інтерпретації результатів, та застосуванні безкоштовного статистичного програмного забезпечення[en].[69]
Статистичні обчислення[ред. | ред. код]
Детальніші відомості з цієї теми ви можете знайти в статті Обчислювальна статистика[en].
На практику статистичної науки, починаючи з другої половини XX сторіччя, суттєво вплинуло швидке й стійке зростання обчислювальної потужності. Ранні статистичні моделі майже завжди походили з класу лінійних моделей[en], але потужні комп'ютери, в поєднанні з відповідними чисельними алгоритмами, спричинили зростання зацікавлення нелінійними моделями[en] (такими як нейронні мережі), а також створення нових типів, таких як узагальнені лінійні[en] та багаторівневі моделі[en].
Збільшення обчислювальної потужності також призвело до зростання популярності обчислювально містких методів, що ґрунтуються на перевибиранні[en], таких як пермутаційний тест та натяжка, тоді як такі методики, як вибирання за Ґіббсом[en], зробили здійсненнішим застосування баєсових моделей. Комп'ютерна революція має наслідки для майбутнього статистики з новим акцентом на «експериментальній» та «емпіричній» статистиці. Наразі є доступною велика кількість статистичного програмного забезпечення[en] як загального, так і спеціального призначення. До прикладів доступного програмного забезпечення, здатного до складних статистичних обчислень, належать такі програми як Mathematica, SAS[en], SPSS та R.
Застосування статистики в математиці та мистецтві[ред. | ред. код]
Традиційно статистика займалася висновуванням із застосуванням напівстандартизованої методології, що була «обов'язковою для вивчення» в більшості наук.[джерело?] Ця традиція змінилася із застосуванням статистики в не висновувальних контекстах. На те, що колись було нудною темою, обов'язковою для отримання ступеня в багатьох галузях, тепер дивляться з ентузіазмом.[на чию думку?] Висміювану спершу деякими математичними пуристами, її тепер вважають важливою методологією в певних областях.
- В теорії чисел точкові діаграми даних, породжуваних функцією розподілу, може бути перетворювано за допомогою звичних інструментів, які використовують у статистиці, щоби розкривати закономірності, що лежать в їх основі, що може потім вести до гіпотез.
- Методи статистики, включено з передбачувальними методами в прогнозуванні, поєднують з теорією хаосу та фрактальною геометрією, щоби створювати, як вважається, дуже красиві відео.[джерело?]
- Живопис процесу[en] Джексона Поллока покладався на живописові експерименти, завдяки яким художньо розкривалися розподіли, що лежать в основі природи.[джерело?] З появою комп'ютерів для формалізування таких ведених розподілами природних процесів було застосовано статистичні методи для створення та аналізу анімованого відеомистецтва.[джерело?]
- Методи статистики можуть використовувати предикативно в мистецтві перформансу, як-от у фокусі з гральними картами, заснованому на марковському процесі, що працює лише деякий час, настання якого можливо передбачувати, використовуючи статистичну методологію.
- Статистику можливо використовувати для предикативного створювання творів мистецтва, як у статистичній або стохастичній музиці, винайденій Янісом Ксенакісом, де музика є залежною від кожного виконання. І хоч цей тип мистецтва не завжди виходить таким, як очікувалося, він поводиться таким чином, що є передбачуваним та налаштовуваним із застосуванням статистики.
Спеціалізовані дисципліни[ред. | ред. код]
Статистичні методики використовують в широкому спектрі типів наукових та суспільних досліджень, включно з біологічною статистикою, обчислювальною біологією, обчислювальною соціологією, мережною біологією[en], суспільствознавством, соціологією та суспільствознавчими дослідженнями. В деяких областях досліджень прикладну статистику використовують настільки широко, що вони мають спеціалізовану термінологію. До цих дисциплін належать:
- Актуарна математика (оцінює ризик в страховій та фінансовій галузях)
- Астрономічна статистика[en] (статистичне оцінювання астрономічних даних)
- Біологічна статистика
- Географія та геоінформаційні системи, конкретно в просторовім аналізі
- Демографія (статистичне дослідження населення)
- Добування даних (застосування статистики та розпізнавання образів для виявляння знань в даних)
- Економетрія (статистичний аналіз економічних даних)
- Епідеміологія (статистичний аналіз захворюваності)
- Медична статистика[71]
- Наука про дані
- Обробка зображень
- Політологія
- Прикладна інформаційна економіка
- Психологічна статистика[en]
- Соціальна статистика[en]
- Статистика енергетики[en]
- Статистична механіка
- Техніка забезпечення надійності[en]
- Хемометрія (для аналізу даних у хімії)
- Юриметрія[en] (право)
- Фізичне виховання та спорт[72]
Крім того, існують певні типи статистичного аналізу, в яких також було розроблено свою власну спеціалізовану термінологію та методологію:
- Аналіз виживаності
- Багатовимірна статистика
- Методологія опитування
- Моделювання структурними рівняннями[en]
- Натяжкова / складано-ножева перевибірка[en]
- Статистична класифікація
- Структурний аналіз даних[en]
- Статистика в багатьох видах спорту, зокрема, у бейсболі[en], відома як саберметрика[en], та крикеті[en]
- Методи Тагучі
Статистика також є ключовим базовим інструментом у бізнесі та виробництві. Її використовують для розуміння варіативності систем вимірювання, керування процесами (як у статистичнім керуванні процесами, англ. statistical process control, SPC), узагальнювання даних, та для здійснення керованих даними рішень. В цих ролях вона є ключовим, і, можливо, єдиним надійним інструментом.
Див. також[ред. | ред. код]
- Оцінювання чисельності[en]
- Наука про дані
- Глосарій теорії ймовірностей та статистики[en]
- Список академічних статистичних асоціацій[en]
- Список важливих публікацій в області статистики[en]
- Перелік національних та міжнародних статистичних служб[en]
- Список статистичних пакетів[en] (програмного забезпечення)
- Список статей зі статистики[en]
- Список університетських статистичних консультаційних центрів[en]
- Позначення в теорії ймовірностей та статистиці[en]
- Всесвітній день статистики
- Засади та головні області статистики
- Засади статистики[en]
- Список статистиків[en]
- Офіційна статистика[en]
- Багатовимірний дисперсійний аналіз[en]
Література[ред. | ред. код]
- Карташов М. В. Імовірність, процеси, статистика. — Київ : ВПЦ Київський університет, 2007. — 504 с.
- Lydia Denworth, «A Significant Problem: Standard scientific methods are under fire. Will anything change?», Scientific American, vol. 321, no. 4 (October 2019), pp. 62–67. (англ.) «Використання p-значень протягом майже сторіччя [з 1925 року] для визначення статистичної значущості результатів експериментів посприяло ілюзії впевненості та кризі відтворюваності в багатьох наукових галузях. Існує все більша рішучість до реформування статистичного аналізу… Деякі [дослідники] пропонують змінювати статистичні методи, тоді як інші покінчили би з порогом для визначення „значущих“ результатів.» (с. 63)
- Barbara Illowsky; Susan Dean (2014). Introductory Statistics. OpenStax CNX. ISBN 9781938168208. Архів оригіналу за 21 липня 2021. Процитовано 13 вересня 2020. (англ.)
- Stockburger, David W. Introductory Statistics: Concepts, Models, and Applications. Missouri State University[en] (вид. 3rd Web). Архів оригіналу за 28 травня 2020. (англ.)
- OpenIntro Statistics [Архівовано 16 червня 2019 у Wayback Machine.], 3rd edition by Diez, Barr, and Cetinkaya-Rundel (англ.)
- Stephen Jones, 2010. Statistics in Psychology: Explanations without Equations [Архівовано 27 липня 2020 у Wayback Machine.]. Palgrave Macmillan. ISBN 9781137282392. (англ.)
- Cohen, J (1990). Things I have learned (so far) (PDF). American Psychologist. 45: 1304—1312. doi:10.1037/0003-066x.45.12.1304. Архів оригіналу (PDF) за 18 жовтня 2017. (англ.)
- Gigerenzer, G (2004). Mindless statistics. Journal of Socio-Economics. 33: 587—606. doi:10.1016/j.socec.2004.09.033. (англ.)
- Ioannidis, J.P.A. (2005). Why most published research findings are false. PLoS Medicine. 2: 696—701. doi:10.1371/journal.pmed.0040168. PMC 1855693. PMID 17456002.
{{cite journal}}: Обслуговування CS1: Сторінки із непозначеним DOI з безкоштовним доступом (посилання) (англ.) - Нариси з історії статистики України / Авт. кол.: О. Г. Осауленко (гол. ред.), В. І. Карпов, М. В. Пугачова та ін.; Держкомстат України, НДІ статистики. — 2-е вид., випр. та доп. — К., 1999. — 188 с.: іл. — Бібліогр.: с. 147—152 (133 назви).
- Статистика: навчальний посібник / С. О. Матковский, М. Л. Вдовин, Т. В. Панчишин. — Львів: Видавничий центр ЛНУ імені Івана Франка, 2010. — 344 с.
- Статистика: навч. посіб. для студ. екон. спец. вищ. навч. закл. / С. О. Матковський, Л. І. Гальків, О. С. Гринькевич, О. З. Сорочак. — 2-ге вид., доповн. і виправл. — Л. : Новий Світ-2000, 2011. — 429, [3] с. : іл. — (Вища освіта в Україні). — Бібліогр. в кінці розділів. — ISBN 978-966-418-089-1
- Статистика: навч. посіб. / Р. В. Фещур, В. П. Кічор, А. Ф. Барвінський, М. Р. Тимощук ; М-во освіти і науки України, Нац. ун-т «Львів. політехніка». — 4-те вид., оновл. і доповн. — Л. : Бух. центр «Ажур», 2010. — 256 с. : іл., табл. — Бібліогр.: с. 251—252 (20 назв). — ISBN 978-966-1688-05-5
- Статистика ринку товарів та послуг: Навч. посіб. / Л. І. Крамченко; Укоопспілка. — Л., 2002. — 188 c. — Бібліогр.: 32 назви.
Посилання[ред. | ред. код]
- (Електронна версія): TIBCO Software Inc. (2020). Data Science Textbook [Архівовано 14 серпня 2020 у Wayback Machine.]. (англ.)
- Online Statistics Education: An Interactive Multimedia Course of Study [Архівовано 15 серпня 2020 у Wayback Machine.]. (англ.) Розроблено Університетом Райса (провідний розробник), Університетом Г'юстона — Клір Лейк[en], Університетом Тафтса та Національним науковим фондом США.
- UCLA Statistical Computing Resources (англ.)
- Philosophy of Statistics [Архівовано 1 листопада 2020 у Wayback Machine.] від Стенфордської філософської енциклопедії (англ.)
- Орлов А. И. Прикладная статистика. Учебник [Архівовано 4 квітня 2013 у Wayback Machine.]. — М.: Издательство «Экзамен», 2004. — 656 с. (рос.)
- Учебно-методический комплекс дисциплины «Статистика» — часть 2(рос.)
Примітки[ред. | ред. код]
- ↑ Oxford Reference. Архів оригіналу за 3 вересня 2020. Процитовано 13 вересня 2020. (англ.)
- ↑ Romijn, Jan-Willem (2014). Philosophy of statistics. Stanford Encyclopedia of Philosophy. Архів оригіналу за 19 жовтня 2021. Процитовано 13 вересня 2020. (англ.)
- ↑ Cambridge Dictionary. Архів оригіналу за 22 листопада 2020. Процитовано 13 вересня 2020. (англ.)
- ↑ а б Статистика [Архівовано 2 грудня 2020 у Wayback Machine.] // Юридична енциклопедія : [у 6 т.] / ред. кол.: Ю. С. Шемшученко (відп. ред.) [та ін.]. — К. : Українська енциклопедія ім. М. П. Бажана, 2003. — Т. 5 : П — С. — 736 с. — ISBN 966-7492-05-2.
- ↑ Dodge, Y. (2006) The Oxford Dictionary of Statistical Terms, Oxford University Press. ISBN 0-19-920613-9 (англ.)
- ↑ Lund Research Ltd. Descriptive and Inferential Statistics. statistics.laerd.com. Архів оригіналу за 26 жовтня 2020. Процитовано 23 березня 2014. (англ.)
- ↑ Романчиков, В.І. (2007). Основи наукових досліджень. Навчальний посібник (PDF). К.: Центр учбової літератури. с. 132, 146. Архів оригіналу (PDF) за 29 листопада 2020. Процитовано 13 вересня 2020.
- ↑ What Is the Difference Between Type I and Type II Hypothesis Testing Errors?. About.com Education. Архів оригіналу за 27 лютого 2017. Процитовано 27 листопада 2015. (англ.)
- ↑ а б в Broemeling, Lyle D. (1 листопада 2011). An Account of Early Statistical Inference in Arab Cryptology. The American Statistician. 65 (4): 255—257. doi:10.1198/tas.2011.10191. (англ.)
- ↑ а б Singh, Simon (2000). The code book : the science of secrecy from ancient Egypt to quantum cryptography (вид. 1st Anchor Books). New York: Anchor Books. ISBN 978-0-385-49532-5. (англ.)
- ↑ а б Ibrahim A. Al-Kadi «The origins of cryptology: The Arab contributions», Cryptologia[en], 16(2) (April 1992) pp. 97–126. (англ.)
- ↑ How to Calculate Descriptive Statistics. Answers Consulting. 3 лютого 2018. Архів оригіналу за 21 липня 2018. Процитовано 13 вересня 2020. (англ.)
- ↑ Moses, Lincoln E. (1986) Think and Explain with Statistics, Addison-Wesley, ISBN 978-0-201-15619-5. pp. 1–3 (англ.)
- ↑ Hays, William Lee, (1973) Statistics for the Social Sciences, Holt, Rinehart and Winston, p.xii, ISBN 978-0-03-077945-9 (англ.)
- ↑ Moore, David (1992). Teaching Statistics as a Respectable Subject. У F. Gordon; S. Gordon (ред.). Statistics for the Twenty-First Century. Washington, DC: The Mathematical Association of America. с. 14–25. ISBN 978-0-88385-078-7. (англ.)
- ↑ Chance, Beth L.; Rossman, Allan J. (2005). Preface (PDF). Investigating Statistical Concepts, Applications, and Methods. Duxbury Press. ISBN 978-0-495-05064-3. Архів оригіналу (PDF) за 22 листопада 2020. Процитовано 13 вересня 2020. (англ.)
- ↑ Lakshmikantham, ed. by D. Kannan, V. (2002). Handbook of stochastic analysis and applications. New York: M. Dekker. ISBN 0824706609. (англ.)
- ↑ Schervish, Mark J. (1995). Theory of statistics (вид. Corr. 2nd print.). New York: Springer. ISBN 0387945466. (англ.)
- ↑ Willcox, Walter (1938) "The Founder of Statistics". Review of the International Statistical Institute 5(4): 321–328. JSTOR 1400906 (англ.)
- ↑ J. Franklin, The Science of Conjecture: Evidence and Probability before Pascal, Johns Hopkins Univ Pr 2002 (англ.)
- ↑ Helen Mary Walker (1975). Studies in the history of statistical method. Arno Press. ISBN 9780405066283. Архів оригіналу за 27 липня 2020. Процитовано 13 вересня 2020. (англ.)
- ↑ Galton, F (1877). Typical laws of heredity. Nature. 15 (388): 492—553. Bibcode:1877Natur..15..492.. doi:10.1038/015492a0. (англ.)
- ↑ Stigler, S.M. (1989). Francis Galton's Account of the Invention of Correlation. Statistical Science. 4 (2): 73—79. doi:10.1214/ss/1177012580. (англ.)
- ↑ Pearson, K. (1900). On the Criterion that a given System of Deviations from the Probable in the Case of a Correlated System of Variables is such that it can be reasonably supposed to have arisen from Random Sampling. Philosophical Magazine. Series 5. 50 (302): 157—175. doi:10.1080/14786440009463897. Архів оригіналу за 18 серпня 2020. Процитовано 13 вересня 2020. (англ.)
- ↑ Karl Pearson (1857–1936). Department of Statistical Science – University College London. Архів оригіналу за 25 вересня 2008. (англ.)
- ↑ Fisher|1971|loc=Chapter II. The Principles of Experimentation, Illustrated by a Psycho-physical Experiment, Section 8. The Null Hypothesis (англ.)
- ↑ OED quote: 1935 R.A. Fisher, The Design of Experiments[en] ii. 19, "We may speak of this hypothesis as the 'null hypothesis', and the null hypothesis is never proved or established, but is possibly disproved, in the course of experimentation." (англ.)
- ↑ Box, JF (February 1980). R.A. Fisher and the Design of Experiments, 1922–1926. The American Statistician[en]. 34 (1): 1—7. doi:10.2307/2682986. JSTOR 2682986. (англ.)
- ↑ Yates, F (June 1964). Sir Ronald Fisher and the Design of Experiments. Biometrics[en]. 20 (2): 307—321. doi:10.2307/2528399. JSTOR 2528399. (англ.)
- ↑ Stanley, Julian C. (1966). The Influence of Fisher's "The Design of Experiments" on Educational Research Thirty Years Later. American Educational Research Journal. 3 (3): 223—229. doi:10.3102/00028312003003223. JSTOR 1161806. (англ.)
- ↑ Agresti, Alan; David B. Hichcock (2005). Bayesian Inference for Categorical Data Analysis (PDF). Statistical Methods & Applications. 14 (3): 298. doi:10.1007/s10260-005-0121-y. Архів оригіналу (PDF) за 19 грудня 2013. Процитовано 13 вересня 2020. (англ.)
- ↑ Edwards, A.W.F. (1998). Natural Selection and the Sex Ratio: Fisher's Sources. American Naturalist. 151 (6): 564—569. doi:10.1086/286141. PMID 18811377. (англ.)
- ↑ Fisher, R.A. (1915) The evolution of sexual preference. Eugenics Review (7) 184:192 (англ.)
- ↑ Fisher, R.A. (1930) The Genetical Theory of Natural Selection[en]. ISBN 0-19-850440-3 (англ.)
- ↑ Edwards, A.W.F. (2000) Perspectives: Anecdotal, Historial and Critical Commentaries on Genetics. The Genetics Society of America (154) 1419:1426 (англ.)
- ↑ Andersson, Malte (1994). Sexual Selection. Princeton University Press. ISBN 0-691-00057-3. Архів оригіналу за 27 липня 2020. Процитовано 13 вересня 2020. (англ.)
- ↑ Andersson, M. and Simmons, L.W. (2006) Sexual selection and mate choice. Trends, Ecology and Evolution (21) 296:302 (англ.)
- ↑ Gayon, J. (2010) Sexual selection: Another Darwinian process. Comptes Rendus Biologies (333) 134:144 (англ.)
- ↑ Neyman, J (1934). On the two different aspects of the representative method: The method of stratified sampling and the method of purposive selection. Journal of the Royal Statistical Society[en]. 97 (4): 557—625. doi:10.2307/2342192. JSTOR 2342192. (англ.)
- ↑ Science in a Complex World – Big Data: Opportunity or Threat?. Santa Fe Institute. Архів оригіналу за 30 травня 2016. Процитовано 13 вересня 2020. (англ.)
- ↑ Wolfram, Stephen (2002). A New Kind of Science. Wolfram Media, Inc. с. 1082. ISBN 1-57955-008-8. (англ.)
- ↑ Freedman, D.A.[en] (2005) Statistical Models: Theory and Practice, Cambridge University Press. ISBN 978-0-521-67105-7 (англ.)
- ↑ McCarney R, Warner J, Iliffe S, van Haselen R, Griffin M, Fisher P (2007). The Hawthorne Effect: a randomised, controlled trial. BMC Med Res Methodol. 7 (1): 30. doi:10.1186/1471-2288-7-30. PMC 1936999. PMID 17608932.
{{cite journal}}: Обслуговування CS1: Сторінки із непозначеним DOI з безкоштовним доступом (посилання) (англ.) - ↑ Rothman, Kenneth J; Greenland, Sander; Lash, Timothy, ред. (2008). 7. Modern Epidemiology (English) (вид. 3rd). Lippincott Williams & Wilkins. с. 100. (англ.)
- ↑ Mosteller, F.; Tukey, J.W (1977). Data analysis and regression. Boston: Addison-Wesley. (англ.)
- ↑ Nelder, J.A.[en] (1990). The knowledge needed to computerise the analysis and interpretation of statistical information. In Expert systems and artificial intelligence: the need for information about data. Library Association Report, London, March, 23–27. (англ.)
- ↑ Chrisman, Nicholas R (1998). Rethinking Levels of Measurement for Cartography. Cartography and Geographic Information Science. 25 (4): 231—242. doi:10.1559/152304098782383043. (англ.)
- ↑ van den Berg, G. (1991). Choosing an analysis method. Leiden: DSWO Press (англ.)
- ↑ Hand, D.J. (2004). Measurement theory and practice: The world through quantification. London: Arnold. (англ.)
- ↑ Mann, Prem S. (1995). Introductory Statistics (вид. 2nd). Wiley. ISBN 0-471-31009-3. (англ.)
- ↑ Силабус навчальної дисципліни «Прикладна економетрія» для магістрів 1-го курсу (PDF). Сумський державний університет, Кафедра прикладної математики та моделювання складних систем факультету електроніки та інформаційних технологій. Архів оригіналу (PDF) за 29 серпня 2020. Процитовано 30 серпня 2020.
- ↑ Upton, G., Cook, I. (2008) Oxford Dictionary of Statistics, OUP. ISBN 978-0-19-954145-4. (англ.)
- ↑ а б Piazza Elio, Probabilità e Statistica, Esculapio 2007 (італ.)
- ↑ Everitt, Brian (1998). The Cambridge Dictionary of Statistics. Cambridge, UK New York: Cambridge University Press. ISBN 0521593468. (англ.)
- ↑ Cohen (1994) The Earth Is Round (p < .05). YourStatsGuru.com. Архів оригіналу за 5 вересня 2015. Процитовано 13 вересня 2020. (англ.)
- ↑ Rubin, Donald B.; Little, Roderick J.A., Statistical analysis with missing data, New York: Wiley 2002 (англ.)
- ↑ Ioannidis, J.P.A. (2005). Why Most Published Research Findings Are False. PLOS Medicine. 2 (8): e124. doi:10.1371/journal.pmed.0020124. PMC 1182327. PMID 16060722.
{{cite journal}}: Обслуговування CS1: Сторінки із непозначеним DOI з безкоштовним доступом (посилання) (англ.) - ↑ Ратинський, В.В. (2013). Використання conjoint-аналізу на ринку світлих нафтопродуктів (PDF). Інноваційна економіка. 47 (9). Архів оригіналу (PDF) за 5 вересня 2020. Процитовано 5 вересня 2020.
- ↑ а б в Huff, Darrell (1954) How to Lie with Statistics, WW Norton & Company, Inc. New York. ISBN 0-393-31072-8 (англ.)
- ↑ Warne, R. Lazo; Ramos, T.; Ritter, N. (2012). Statistical Methods Used in Gifted Education Journals, 2006–2010. Gifted Child Quarterly. 56 (3): 134—149. doi:10.1177/0016986212444122. (англ.)
- ↑ а б Drennan, Robert D. (2008). Statistics in archaeology. У Pearsall, Deborah M. (ред.). Encyclopedia of Archaeology. Elsevier Inc. с. 2093–2100. ISBN 978-0-12-373962-9. (англ.)
- ↑ а б Cohen, Jerome B. (December 1938). Misuse of Statistics. Journal of the American Statistical Association. JSTOR. 33 (204): 657—674. doi:10.1080/01621459.1938.10502344. (англ.)
- ↑ Freund, J.E. (1988). Modern Elementary Statistics. Credo Reference. (англ.)
- ↑ Huff, Darrell; Irving Geis (1954). How to Lie with Statistics. New York: Norton.
The dependability of a sample can be destroyed by [bias]... allow yourself some degree of skepticism.
(англ.) - ↑ Стентон Гланц Медико-биологическая статистика — М., Практика, 1998. — С.405-406 (рос.)
- ↑ Nikoletseas, M.M. (2014) "Statistics: Concepts and Examples." ISBN 978-1500815684 (англ.)
- ↑ Anderson, D.R.; Sweeney, D.J.; Williams, T.A. (1994) Introduction to Statistics: Concepts and Applications, pp. 5–9. West Group. ISBN 978-0-314-03309-3 (англ.)
- ↑ Journal of Business & Economic Statistics. Journal of Business & Economic Statistics. Taylor & Francis. Архів оригіналу за 27 липня 2020. Процитовано 16 березня 2020. (англ.)
- ↑ а б Natalia Loaiza Velásquez, María Isabel González Lutz & Julián Monge-Nájera (2011). Which statistics should tropical biologists learn? (PDF). Revista Biología Tropical. 59: 983—992. Архів оригіналу (PDF) за 19 жовтня 2020. Процитовано 13 вересня 2020. (англ.)
- ↑ Pekoz, Erol (2009). The Manager's Guide to Statistics. Erol Pekoz. ISBN 9780979570438. (англ.)
- ↑ Медична статистика. Архів оригіналу за 19 січня 2018. Процитовано 18 січня 2018.
- ↑ Aliberti, Sara; D'Elia, Francesca; Cherubini, Domenico (2023). Tips for Statistical Tools for Research Methods in Exercise and Sport Sciences. Physical Education Theory and Methodology. 23(3): 470—477. doi:10.17309/tmfv.2023.3.20. ISSN 1993-7989.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|