Дискретизація
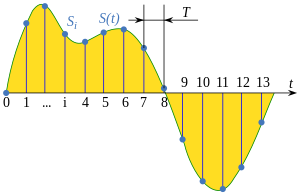
Дискретиза́ція — перетворення функцій неперервних змінних у функції дискретних змінних, за якими початкові неперервні функції можуть бути відновлені із заданою точністю. Роль відліків виконують квантовані значення функцій. Під квантуванням розуміють перетворення неперервної за значеннями величини у величину з дискретною шкалою значень з скінченної множини дозволених, які називають рівнями квантування. Якщо рівні квантування нумеровані, то результатом перетворення є число, яке може бути виражене в будь-якій системі числення.
Для виробничих задач обробки даних зазвичай потрібно значно менше інформації, ніж її надходить від вимірювальних датчиків у вигляді безперервного аналогового сигналу. При статистичних флюктуаціях вимірюваних величин і кінцевої похибки засобів вимірювань інформація про величину сигналу завжди обмежена. Раціональне виконання дискретизації і квантування початкових даних дає можливість знизити витрати на зберігання і обробку інформації. Використання дискретних сигналів дозволяє застосовувати методи кодування інформації з можливістю подальшого виявлення та виправлення помилок при зверненні до збереженої інформації. Цифрова форма сигналів полегшує також уніфікацію операцій перетворення інформації на всіх етапах звернення до неї.
Історія[ред. | ред. код]
У першій половині ХХ століття при реєстрації та обробці інформації використовувалися, в основному, вимірювальні прилади та пристрої аналогового типу, що працюють в реальному масштабі часу, при цьому навіть для величин, дискретних в силу своєї природи, застосовувалося перетворення дискретних сигналів в аналогову форму. Положення змінилося з поширенням мікропроцесорної техніки та ЕОМ. Цифрова реєстрація та обробка інформації виявилася більш досконалою і точною, більш універсальною, багатофункціональною і гнучкою. Міць і простота цифрової обробки сигналів настільки переважають над аналоговою, що перетворення аналогових за природою сигналів в цифрову форму давно стало виробничим стандартом.
Під дискретизацією сигналів розуміють перетворення функцій безперервних змінних у функції дискретних змінних, за якими вихідні безперервні функції можуть бути відновлені з заданою точністю. Роль дискретних відліків виконують, як правило, квантовані значення функцій в дискретної шкалою координат. Під квантуванням розуміють перетворення неперервної за значеннями величини у величину з дискретною шкалою значень з кінцевого безлічі дозволених, які називають рівнями квантування. Якщо рівні квантування нумеровані, то результатом перетворення є число, яке може бути виражене у будь-якій числовій системі. Округлення з певною розрядністю миттєвих значень неперервної аналогової величини з рівномірним кроком по аргументу є найпростішим випадком дискретизації і квантування сигналів при їх перетворенні в цифрові сигнали.
Для виробничих завдань обробки даних зазвичай потрібно значно менше інформації, ніж її надходить від вимірювальних датчиків у вигляді безперервного аналогового сигналу. При статистичних флуктуаціях вимірюваних величин і кінцевої похибки засобів вимірювань інформація про величину сигналу завжди обмежена. Раціональне виконання дискретизації і квантування вихідних даних дає можливість знизити витрати на зберігання і обробку інформації. Використання цифрових сигналів дозволяє застосовувати методи кодування інформації з можливістю подальшого виявлення та виправлення помилок при зверненні інформації. Цифрова форма сигналів полегшує також уніфікацію операцій перетворення інформації на всіх етапах її обігу.
Див. також[ред. | ред. код]

|
Це незавершена стаття з технології. Ви можете допомогти проєкту, виправивши або дописавши її. |
| Ця стаття не містить посилань на джерела. (березень 2015) |