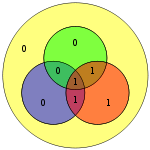
Гемінг(7,4)

Графічне подання 4 бітів даних інформації D1-D4 і 3 бітів парності Р1-Р3

В теорії кодування, метод Гемінг(7,4) — лінійний код, що кодує чотири біта даних в сім бітів, додавши три біта для підтвердження парності. Він є членом великої родини кодів Гемінга, але термін код Гемінга часто посилається на цей метод, який Річард Гемінг відкрив у 1950 році. Працюючи у компанії Bell Labs, Гемінг постійно стикався з помилками читання перфокарт, тому й почав працювати над кодом, що виправляє ці помилки.

Код Гемінга додає три додаткові біти парності на кожні чотири біта даних повідомлення. Алгоритм Гемінг(7,4) може виправляти всі одно-бітові помилки.

Мета

Метод Гемінг(7,4) створює ряд бітів парності, які накладаються таким чином, що одно-бітова помилка (біт, дзеркально відображений в значенні) у біті даних або біті парності може бути виявлена і виправлена.

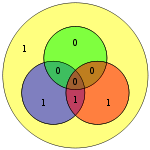
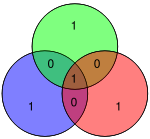
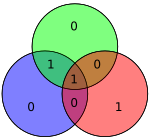
Гемінг(7,4) створює набір з 3-х бітів парності так, щоб при втраті інформації при передачі можна було відновити один з 4х бітів інформації.

Біт #	1	2	3	4	5	6	7
Переданий біт	$p_{1}$	$p_{2}$	$d_{1}$	$p_{3}$	$d_{2}$	$d_{3}$	$d_{4}$
$p_{1}$	Так	Ні	Так	Ні	Так	Ні	Так
$p_{2}$	Ні	Так	Так	Ні	Ні	Так	Так
$p_{3}$	Ні	Ні	Ні	Так	Так	Так	Так

Ця таблиця описує, які біти парності перекривають біти даних. Наприклад, p2 забезпечує рівну парність для бітів 2, 3, 6, і 7, d1 покритий p1, і у p2, але не p3

Багаторазові бітові помилки

Помилка у біті 4 та 5 представлена (показано в синьому тексті) з порушенням парності тільки в зеленому колі (показано в червоному тексті)

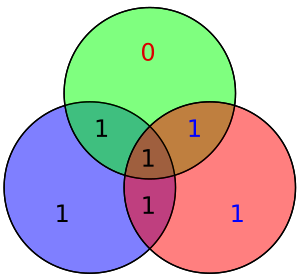
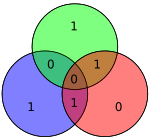
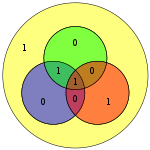
Очевидно, що в даному методі можуть бути виправлені тільки одно-бітові помилки. Альтернативно, коди Гемінга можуть використовуватися, щоб виявити одно- і дво-бітові помилки. У діаграмі поруч були дзеркально відображені біти 4 і 5. Це призводить тільки до однієї помилки парності (в зеленому колі), але така помилка є невідновлювальною.

Однак Гемінг(7,4) і подібні коди Гемінга не можуть розрізняти одно- і дво-бітові помилки. Тобто дво-бітові помилки виявляються як одно-бітові. Якщо корекція помилок буде виконуватися на дво-бітові помилку, то результат буде неправильним.

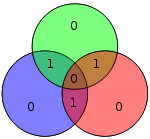
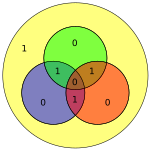
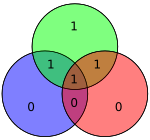
Так само метод Гемінг(7,4) не може виправити трьох-бітові помилки. Розгляньте схему: якби біт в зеленому колі (забарвлений в червоний) дорівнював 1, перевірка парності повернула б нульовий вектор, вказавши, що немає ніякої помилки в кодовій комбінації.

Кодові комбінації

Оскільки метод Гемінг(7,4) містить лише 4 біта даних, є тільки 16 можливих переданих слів. Біти даних показані в синьому; біти парності показані в червоному, і додатковий біт парності, показаний в зеленому:

Дані $({\color {blue}d_{1}},{\color {blue}d_{2}},{\color {blue}d_{3}},{\color {blue}d_{4}})$	Гемінг(7,4)		Гемінг(7,4) з додатковим бітом парності (Гемінг(8,4))
	Слово $({\color {red}p_{1}},{\color {red}p_{2}},{\color {blue}d_{1}},{\color {red}p_{3}},{\color {blue}d_{2}},{\color {blue}d_{3}},{\color {blue}d_{4}})$	Діаграма	Слово $({\color {red}p_{1}},{\color {red}p_{2}},{\color {blue}d_{1}},{\color {red}p_{3}},{\color {blue}d_{2}},{\color {blue}d_{3}},{\color {blue}d_{4}},{\color {green}p_{4}})$	Діаграма
0000	0000000		00000000
1000	1110000		11100001
0100	1001100		10011001
1100	0111100		01111000
0010	0101010		01010101
1010	1011010		10110100
0110	1100110		11001100
1110	0010110		00101101
0001	1101001		11010010
1001	0011001		00110011
0101	0100101		01001011
1101	1010101		10101010
0011	1000011		10000111
1011	0110011		01100110
0111	0001111		00011110
1111	1111111		11111111