Неможлива фігура
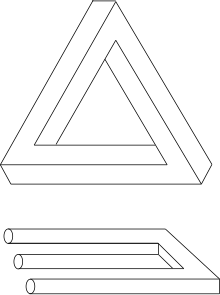
Неможлива фігура — один з видів оптичних ілюзій, фігура, що здається на перший погляд проекцією звичайного тривимірного об'єкта, але якщо придивитися, то стають очевидні суперечливі поєднання елементів фігури. Створюється ілюзія неможливості існування такої фігури в тривимірному просторі.
Насправді всі неможливі фігури можуть існувати в реальному світі. Так всі об'єкти, намальовані на папері, є проекціями тривимірних об'єктів, отже, можна створити такий тривимірний об'єкт, який при проектуванні на площину буде виглядати неможливим. При погляді на такий об'єкт з певної точки він також буде виглядати неможливим, але при погляді з будь-якої іншої точки ефект неможливості буде втрачатися.
Найбільш відомі неможливі фігури: неможливий трикутник, нескінченні сходи і неможливий тризуб . «Батьком» неможливих фігур є шведський художник Оскар Реутерсвард, який за роки своєї творчості намалював тисячі таких фігур. Справжню популярність неможливі фігури здобули, коли їх зобразив на своїх літографіях відомий голландський художник Мауріц Корнеліс Ешер .
Напрям в образотворчому мистецтві, спрямований на зображення неможливих фігур, називається імп-арт . Найбільш відоме використання неможливих фігур в масовій культурі — логотип автоконцерну " Рено ".
Галерея [ред.]
-
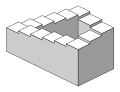
Неможливий куб
Література [ред.]
- M. C. Escher: Grafiek en Tekeningen. Koninklijke Erven, Zwolle 1959. IX Konfliekt
- Bruno Ernst: Abenteuer mit unmöglichen Figuren. Taco, Berlin 1987. ISBN 3-89268-012-4
- Bruno Ernst, Optical Illusions, 2006 ISBN 3-8228-5410-7
- Martin Gardner, Mathematical Circus, 1979 ISBN 0-14-022355-X (Chapter 1 — Optical Illusions)
Посилання [ред.]
 |
ВікіСховище має мультимедійні дані за темою: Неможлива фігура |
