Миттєвий центр швидкостей

Миттє́вим це́нтром швидкосте́й (МЦШ) називається точка рухомої плоскої фігури, що здійснює плоскопаралельний рух, швидкість якої в даний момент часу дорівнює нулю . Вказана точка може бути розташована або на самій рухомій фігурі, або на її уявному продовженні.
Доведення[ред. | ред. код]

Нехай задано фігуру S, що здійснює плоский рух і швидкість деякої точки А цієї фігури вважається відомою а також, кутова швидкість обертання фігури.
Якщо побудувати у точці А перпендикуляр до вектора швидкості , який напрямлений у бік отриманий поворотом вектора швидкості за напрямком обертання фігури і відкласти на цьому перпендикулярі відрізок довжиною , то обравши точку А за полюс, швидкість точки Р даної фігури буде визначатись за допомогою наступного векторного рівняння:
- .
З цього виразу знайдемо швидкість . Вона буде дорівнювати:
- .
Вектор швидкості буде спрямований протилежно до вектора швидкості , тобто
- .
Тоді, з врахуванням цього, з виразу для швидкості точки P отримаємо:
Таким чином, швидкість точки P дорівнює нулю, чим і доведено існування миттєвого центру швидкостей (МЦШ).
Можна довести, що при плоскопаралельному непоступальному русі плоскої фігури в кожний момент часу існує, і при тому єдина, точка з нульовою швидкістю.
Абсолютні значення швидкостей всіх точок плоскої фігури будуть прямо пропорційними їх відстаням до МЦШ, а напрями векторів швидкостей будуть перпендикулярними до прямих, які з'єднують ці точки з МЦШ. Саме тому МЦШ називають також миттєвим центром обертання.
Теорема Ейлера-Шаля[ред. | ред. код]
Рух плоскої фігури в її площині уявляється як неперервна послідовність миттєвих обертань навколо відповідних миттєвих центрів обертань (МЦО). За теоремою Ейлера-Шаля плоский рух уявляється як обертальний рух навколо миттєвого центра обертань, або центра швидкостей.
Миттєвим центром обертань є точка нерухомої площини, з якою у даний момент часу збігається миттєвий центр швидкостей (МЦШ).
Згідно з теоремою обертання Ейлера, будь-яке обертове тривимірне тіло, що має нерухому точку, також має і вісь обертання. Таким чином, у загальнішому випадку обертання тривимірного тіла говорять про миттєву вісь обертання. Миттєвий центр обертання є точкою перетину миттєвої осі обертань з площиною руху.
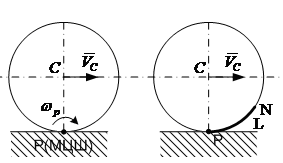
Будь-який неперервний рух плоскої фігури в її площині можна одержати, якщо побудувати рухому і нерухому центроїди, жорстко з'єднати першу з них з плоскою фігурою і котити без ковзання рухому центроїду по нерухомій.
Центроїдою називається геометричне місце миттєвих центрів швидкостей (МЦШ).
При плоскопаралельному русі утворюються дві центроїди, оскільки миттєвий центр швидкостей описує одну криву в нерухомій системі координат, а другу в рухомій. Нерухома центроїда — це траєкторія миттєвого центра швидкостей на нерухомій площині, рухома центроїда — це траєкторія миттєвого центра швидкостей на рухомій площині. Рухома центроїда PN котиться без ковзання по нерухомій PL (див. рисунок). Поняття про центроїди широко застосовується у теорії машин і механізмів при профілюванні зубчатих коліс.
Полюсом є миттєвий центр швидкостей (МЦШ), тобто така точка Р рухомої площини, жорстко скріплена з фігурою, швидкість якої в певний момент часу дорівнює нулю: .
Тоді , тобто швидкість будь-якої точки фігури дорівнює за величиною добутку модуля кутової швидкості фігури на відстань від цієї точки до МЦШ та спрямована перпендикулярно до цього відрізку проти ходу годинникової стрілки, якщо і навпаки.
Розподіл миттєвих швидкостей точок плоскої фігури такий, немовби фігура оберталася навколо МЦШ (точка Р). З цього маємо співвідношення
. Отже, відношення швидкостей двох точок плоскої фігури дорівнює відношенню їхніх відстаней до миттєвого центра швидкостей, або
Випадки знаходження миттєвого центра швидкостей плоскої фігури[ред. | ред. код]
Випадок 1 (загальний)[ред. | ред. код]
У загальному випадку (див. рисунок вгорі) для знаходження МЦШ потрібно знати лише напрям швидкостей двох точок фігури. Для цього з початку векторів швидкостей зазначених двох точок (наприклад А, В і C) проводимо перпендикуляри. У точці перетину цих перпендикулярів і знаходиться миттєвий центр швидкостей (точка Р).
Кутова швидкість плоскої фігури у кожний момент часу дорівнює відношенню швидкості будь-якої точки фігури до її відстані до МЦШ:

Випадок 2 (для двох паралельних однонаправлених швидкостей)[ред. | ред. код]
Відомі за величиною швидкості двох точок А і В фігури, які паралельні одна одній, напрямлені в один бік і перпендикулярні до прямої АВ (варіант а на рисунку).
МЦШ (точка Р) знаходиться в точці перетину прямої АВ і прямої, що з'єднує кінці векторів швидкостей точок А і В:
Випадок 3 (для двох протилежно направлених паралельних швидкостей)[ред. | ред. код]
Якщо швидкості двох точок плоскої фігури напрямлені в різні боки і перпендикулярні до відрізка, що з'єднує ці точки, то миттєвий центр швидкостей лежить у точці перетину прямої, яка з'єднує кінці векторів швидкостей з наведеним вище відрізком (варіант б на рисунку).
Випадок 4 (для двох однакових паралельних однаково направлених швидкостей)[ред. | ред. код]
Якщо швидкості двох точок плоскої фігури паралельні й рівні між собою, напрямлені в один бік, то миттєвий центр швидкості віддаляється на нескінченну велику відстань, тобто МЦШ відсутній, , і миттєві швидкості всіх точок фігури рівні між собою: (варіант в на рисунку).
Це випадок миттєво-поступального руху тіла: відстань до МЦШ прямує до нескінченності і .

Випадок 5 (кочення без ковзання)[ред. | ред. код]
У разі кочення без ковзання рухомого контуру плоскої фігури по нерухомому МЦШ лежить у точці дотику цих контурів. Кутова швидкість
Див. також[ред. | ред. код]
Джерела[ред. | ред. код]
- Павловський М. А. Теоретична механіка: Підручник для студентів вищих навчальних закладів. — К.: Техніка, 2002. — 512 с. ISBN 966-575-184-0.
- Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1986. — 416 с.
Посилання[ред. | ред. код]
| Вікісховище має мультимедійні дані за темою: Миттєвий центр швидкостей |





















