Швидкість
| Швидкість | ||||
| Оскільки відбувається неперервна зміна напрямку руху, коли гоночні машини рухаються по криволінійній доріжці, їхня швидкість не є сталою | ||||
| Символи: | ||||
|---|---|---|---|---|
| Одиниці вимірювання | ||||
| Розмірність: | L T−1 | |||
| Одиниці вимірювання: | м/с; m/s | |||
|
| ||||
| Класична механіка |
|---|
| Історія класичної механіки |
|
Фундаментальні поняття Простір · Час · Система відліку · Маса · Інерція · Швидкість · Прискорення · Імпульс · Сила · Гравітація · Момент імпульсу · Момент сили · Момент інерції · Енергія · Кінетична енергія · Потенціальна енергія · Механічна робота · Потужність |
|
Основні принципи |
|
Важливі теми |
|
Формулювання |

Шви́дкість, або погі́н[1], ско́рість[2], ху́ткість[3], пру́дкість[4], бистрота́[5] — фізична величина, що відповідає відношенню переміщення тіла до проміжку часу, за який відбувалося переміщення. Швидкість — величина векторна, тобто вона має значення (модуль) і напрямок.
Швидкість, як векторна величина здебільшого позначається літерою або , а коли йде мова тільки про кількісне значення швидкості — (від лат. Velocitas — швидкість).
У системі SI швидкість (точніше її абсолютна величина) вимірюється в метрах за секунду — м/с. У системі СГС одиницею вимірювання швидкості є сантиметр за секунду — см/с. У повсякденному житті найпрактичнішою одиницею вимірювання швидкості є кілометр на годину — км/год. У певних галузях людської діяльності чи країнах використовуються специфічні одиниці швидкості, як-от вузол чи фут за секунду.
У науці використовується також швидкість у широкому значенні, як швидкість зміни будь-якої величини (не обов'язково радіус-вектора) залежно від іншої (частіше зміни в часі, але також у просторі або будь-якої іншої). Так, наприклад, говорять про кутову швидкість, швидкість зміни температури, швидкість хімічної реакції, групову швидкість, швидкості зʼєднання тощо. Математично швидкість характеризується похідною функції.
Способи опису швидкості[ред. | ред. код]
Траєкторний опис[ред. | ред. код]
Нехай тіло, що можна вважати за матеріальну точку, рухається по довільній траєкторії. Шлях, який пройшло тіло за проміжок часу :
- .
За означенням:
- (1), де — середня шляхова швидкість або середнє значення абсолютної величини швидкості за час . Швидкість тіла найлегше визначити тоді, коли воно здійснює рівномірний прямолінійний рух, тобто долає однакові відстані за однакові проміжки часу. У такому разі швидкість визначається як відношення відстані до часу:
де — шлях, пройдений тілом за час .
Визначене таким способом середнє значення абсолютної величини швидкості — скалярна величина і не повʼязана з переміщенням тіла. Наприклад, дівчина, яка пробігла од Полтави до Хорола, а потім повернулася назад, здійснила нульове переміщення, однак вона рухалася з певною середньою швидкістю, скажімо 10 км/год.
Механіка узагальнює поняття «швидкість» для довільного руху, використовуючи математичний апарат аналізу. Загалом тіла рухаються нерівномірно й можуть змінювати напрямок руху. Для опису такого руху вводиться поняття миттєвої швидкості, яку механіка надалі і називає просто швидкістю. Траєкторія руху тіла розбивається на маленькі ділянки, на яких рух можна вважати рівномірним і прямолінійним, і визначається швидкість на цих ділянках. Швидкість тіла в даній точці траєкторії (у певний момент часу) — миттєва швидкість, — буде тим точніше означена відношенням (1), чим менші значення і . У границі, коли прямує до нуля, отримується вираз для модуля миттєвої швидкості:
- .
Отже, миттєву швидкість можна знайти за заданою залежністю через похідну по часу для будь-якого моменту часу. Швидкість — векторна величина. Отже, за означенням:
де — одиничний вектор уздовж дотичної до траєкторії, спрямований у напрямку руху в тій точці, у якій визначається швидкість.
Векторний опис[ред. | ред. код]


Якщо положення матеріальної точки відносно початку відліку задається радіусом-вектором , то для двох послідовних моментів часу і її переміщення характеризуватиметься вектором .
За означенням, середня швидкість матеріальної точки або середня швидкість переміщення довільного руху за інтервал часу — це векторна величина[6][7]:
- ,
де — переміщення тіла за час .
Після застосування граничного переходу вводиться означення миттєвої швидкості.
Миттєва швидкість нерівномірного руху — це вектор у точці, який є границею середніх швидкостей, коли інтервал часу прямує до нуля. Розкриваючи означення, швидкість — це відношення переміщення матеріальної точки за інтервал часу, коли цей інтервал прямує до нуля, тобто похідна за часом від радіуса-вектора точки, що рухається:
- .
Вектор швидкості спрямований у бік руху точки по дотичній до траєкторії її руху.
Так само, похідна від швидкості дає миттєве прискорення тіла в момент часу :
Задання швидкості в різних системах координат[ред. | ред. код]
Проєкції швидкості на осі прямокутної декартової системи координат дорівнюють першим похідним за часом від відповідних координат точки, що рухається:
З цього:
- і, отже .
У циліндричній системі координат
і у сферичній системі координат
Прямолінійний рівноприскорений рух[ред. | ред. код]
Кінцева швидкість обʼєкта з початковою швидкістю та постійним у часі прискоренням в період часу визначається як:
Середня швидкість обʼєкта з постійним прискоренням становить . Тоді для обчислення відстані переміщення тіла за проміжок часу отримаємо формулу:
Якщо відома тільки початкова швидкість, можна застосовувати формулу:
З цих базових рівнянь виводиться формула, не залежна від параметру часу :
Наведені рівняння справедливі як для класичної механіки, так і для спеціальної теорії відносності. Відмінність ситуації полягає, зокрема, у тому, що в класичній механіці для всіх спостерігачів в інерційних системах відліку прискорення тіла, що рухається, буде однаковим. Для спеціальної теорії відносності це не так.
Швидкість точки при обертанні по колу[ред. | ред. код]
Рух матеріальної точки по колу можна охарактеризувати як лінійними кінематичними величинами на основі викладок, зроблених вище, так і кутовими кінематичними величинами — кутовою координатою і кутовою швидкістю .
При обертанні матеріальної точки з кутовою швидкістю по колу радіусом R її миттєва швидкість визначається формулою
Швидкість точки при плоскому русі[ред. | ред. код]

Загалом, якщо розглядати рух матеріальної точки A в площині в полярній системі координат, то швидкість можна розкласти на дві взаємно перпендикулярні складові: радіальну (променеву) й тангенціальну (трансверсальну). Радіальна швидкість направлена вздовж радіус-вектора точки й характеризує віддалення або наближення точки A до початку системи координат O. Тангенціальна швидкість направлена перпендикулярно до радіус-вектора, і характеризує обертання точки А навколо початку відліку О системи координат:
причому
де — полярний радіус-вектор, проведений з полюса в точку, а — одиничний вектор, напрямлений перпендикулярно до площини руху так, що обертання радіус-вектора у бік збільшення кута відбувається проти стрілки годинника. Проєкції радіальної і дотичної швидкостей точки на напрями відповідно радіуса-вектора і прямої, проведеної перпендикулярно до нього в бік зростання кута :
Повне значення швидкості в цьому разі:
Загальний випадок руху твердого тіла[ред. | ред. код]
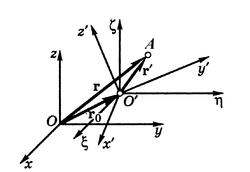
Швидкість поступального і обертального рухів[ред. | ред. код]
Загалом вільне тверде тіло має шість ступенів вільності. Його розташування в просторі визначається трьома координатами якоїсь довільно вибраної точки O' тіла, яку називають полюсом, і трьома кутами Ейлера ψ, θ, φ, які характеризують положення тіла відносно прямокутної декартової системи координат O'ξης, осі якої паралельні до відповідних осей основної (нерухомої) системи координат Oxyz, а початок знаходиться в полюсі O'. Відповідно рух тіла можна розглядати як сукупність двох рухів, що відбуваються одночасно — поступального зі швидкістю полюса O' й обертального навколо полюса з кутовою швидкістю ω, яка не залежить від вибору полюса.
На рисунку показано жорстко звʼязану з тілом рухому систему координат O'x'y'z'. Радіуси-вектори довільної точки A тіла в нерухомій і рухомій системах координат повʼязані співвідношенням:
Швидкість точки A тіла буде дорівнювати:
де — швидкість поступального руху тіла.
Закон додавання швидкостей[ред. | ред. код]
Звʼязок між радіусами-векторами і точки A, що рухається, проведеними відповідно з початку O нерухомої системи відліку (x, y, z) і початку O' рухомої системи (x', y', z'), має вигляд:
де x', y', z' — проєкції на осі рухомої системи, а — орти цих осей.
Абсолютна швидкість точки як похідна по часу від радіус-вектора, дорівнює за умови однаковості перебігу часу в обох системах відліку («абсолютний час»):
- .
У цьому рівнянні:
- перший доданок — швидкість поступального руху рухомої системи;
- наступні три доданки описують зміну в часі ортів , яка може бути зумовлена лише обертанням рухомої системи координат з кутовою швидкістю ω:
- ;
- останні три доданки характеризують відносну швидкість точки .
Отже, де — переносна швидкість точки A, що дорівнює абсолютній швидкості тієї незмінно повʼязаної з рухомою системою відліку точки простору, з якою наразі збігається точка A, що рухається.
Отже, абсолютна швидкість руху точки дорівнює векторній сумі її переносної і відносної швидкостей:
- .
Це положення, на якому базується перетворення Галілея, є справедливим у класичній механіці, але потребує уточнення в релятивістській механіці, де для цього використовується перетворення Лоренца.
Узагальнена швидкість[ред. | ред. код]
У механіці Лагранжа аналогічним чином вводиться узагальнена швидкість :
- ,
де — узагальнена координата, тобто одна з величин, що визначають миттєве положення механічної системи.
Наприклад, при обертанні твердого тіла, узагальнена координата: кут повороту . Узагальнена швидкість — це кутова швидкість:
Теорія відносності[ред. | ред. код]
Основний постулат теорії відносності встановлює максимальну швидкість, з якою може передаватись інформація, а, отже, і рухатися тіло. Ця максимальна швидкість — швидкість світла (мається на увазі швидкість світла у вакуумі) — є універсальною фізичною сталою.
Для опису руху тіл у теорії відносності вводиться 4-вектор швидкості, або 4-швидкість:
- ,
де ds — просторово-часовий інтервал :
- ,
де — звичайна тривимірна швидкість, а c — швидкість світла у вакуумі.
4-швидкість — безрозмірна величина. Для 4-вектора швидкості завжди справедливе рівняння:
Відносна швидкість[ред. | ред. код]
Значення швидкості тіла залежить від системи відліку спостерігача. У класичній механіці, яка використовує принцип Галілея, швидкість тіла в новій системі відліку є векторною різницею його швидкості в старій системі й швидкості нової системи відліку відносно старої :
- ,
де — швидкість тіла в новій системі відліку, — швидкість тіла в старій системі відліку, — швидкість нової системи відліку відносно старої.
У системі відліку, яка рухається з тією самою швидкістю, що й тіло, воно є непорушним.
У теорії відносності наведена формула не є справедливою, оскільки жодне тіло не може рухатися зі швидкістю, яка перевищувала б швидкість світла. Наприклад, у разі, коли напрям швидкості нової системи відліку збігається з напрямком руху тіла, швидкість у новій системі дорівнює
- .
За малих швидкостей або ця формула збігається з формулою перетворень Галілея.
Зв'язок з іншими фізичними величинами[ред. | ред. код]
Тіло, яке рухається з певною швидкістю, має імпульс та енергію. Імпульс матеріальної точки масою , що рухається зі швидкістю , дорівнює
- .
Кінетична енергія такої матеріальної точки в класичній механіці дорівнює
- .
Завдяки кінетичній енергії фізичне тіло, яке має відмінну від нуля швидкість, може здійснювати роботу.
Рівняння руху механіки задають зв'язок між прискоренням тіл та силами, які діють на ці тіла. Отже, вони є диференціальними рівняннями щодо швидкостей. Для опису часової еволюції механічної системи потрібно задати не тільки положення тіл, а і їхні швидкості в початковий момент часу. Наприклад, висота, на яку злетить підкинутий угору м'яч, і час його польоту залежать від того, яку початкову швидкість йому надали.
Деякі характерні швидкості[ред. | ред. код]
Космічні швидкості[ред. | ред. код]
Небесна механіка вивчає поведінку тіл Сонячної системи та інших небесних тіл. Рух штучних космічних тіл вивчається астродинамікою. Водночас розглядається декілька варіантів руху тіл, у кожному з яких тілу слід надати певної швидкості. Для виведення супутника на колову орбіту йому слід надати першої космічної швидкості (наприклад для виведення на орбіту штучного супутника Землі він повинен мати швидкість 7,9 км/с). Подолати гравітаційне притягання дозволить друга космічна швидкість (наприклад, об'єкту запущеному із Землі для подолання її гравітації слід надати швидкість 11,2 км/с). Третя космічна швидкість потрібна для того, щоб покинути зоряну систему, подолавши притяганні зорі (наприклад, об'єкт, що запущений із Землі повинен мати швидкість 16,67 км/с відносно Землі під час старту в найвигіднішому напрямі, а під час старту із Землі в найменш вигідному напрямку його необхідно розігнати до швидкості 72,8 км/с). Четверта космічна швидкість дозволить покинути галактику.
Швидкість звуку[ред. | ред. код]
Швидкість звуку — швидкість поширення пружних хвиль у середовищі і визначається пружністю і густиною середовища. Швидкість звуку не є сталою величиною і залежить від температури (у газах), від напрямку поширення хвилі (у монокристалах) але за заданих зовнішніх умов переважно не залежить від частоти хвилі та її амплітуди. Для випадків, коли ця умова не виконується і швидкість звуку залежить від частоти, кажуть про дисперсію звуку. Вперше швидкість звуку виміряв Вільям Дерхам (англ. William Derham; 1657—1735). У газах швидкість звуку є меншою, ніж у рідинах, а в рідинах швидкість звуку менша за швидкість звуку у твердих тілах.
Відношення швидкості потоку в даній точці газового середовища до місцевої швидкості поширення звуку має назву «Число Маха». Швидкість, що відповідає М1 (1 Маху) при тиску в 1 атм, дорівнюватиме швидкості звуку в повітрі. Рух об'єктів зі швидкістю, порівняльною зі швидкістю звуку, спричиняє проявлення низки явищ, що супроводжують подолання звукового бар'єру. Швидкості від М1,2 до М5 називаються надзвуковими, швидкості понад М5 — гіперзвуковими.
Швидкість світла[ред. | ред. код]

Швидкість світла у вакуумі — абсолютне значення швидкості поширення електромагнітних хвиль у вакуумі. Традиційно позначається літерою латинського алфавіту «c»[8]. Швидкість світла у вакуумі — фізична стала, що не залежить від вибору інерційної системи відліку. Вона належить до фундаментальних фізичних сталих, що характеризують не просто окремі тіла чи поля, а властивості простору-часу загалом. За сучасними уявленнями швидкість світла у вакуумі — гранична швидкість руху і поширення взаємодій.
Точне значення швидкості світла зафіксувала резолюція 117-ї Генеральної конференції мір і ваг[9]:
Швидкість перебігу процесу[ред. | ред. код]
В українській мові термін швидкість уживається також не в механічному сенсі для визначення часових характеристик перебігу довільних процесів: наприклад, швидкість хімічної реакції, швидкість нагрівання, швидкість замерзання, швидкість випаровування. Якщо певний процес характеризується залежною від часу величиною , то миттєва швидкість перебігу цього процесу визначається похідною . Відповідно, середня швидкість за проміжок часу визначається як .
Див. також[ред. | ред. код]
| Вікіцитати містять висловлювання на тему: Швидкість |
| Вікісховище має мультимедійні дані за темою: Швидкість |
- Імпульс
- Прискорення
- Число Маха
- Швидкість звуку
- Космічна швидкість
- Фазова швидкість
- Групова швидкість
- Дисперсія швидкостей
- Швидкість гравітації
Примітки[ред. | ред. код]
- ↑ Тлумачення / значення слова "ПОГІН" | Словник української мови. Словник Грінченка. hrinchenko.com. Процитовано 5 грудня 2022.
- ↑ Тлумачення / значення слова "СКОРІСТЬ" | Словник української мови. Словник Грінченка. hrinchenko.com. Процитовано 5 грудня 2022.
- ↑ Тлумачення / значення слова "ХУТКІСТЬ" | Словник української мови. Словник Грінченка. hrinchenko.com. Процитовано 5 грудня 2022.
- ↑ Тлумачення / значення слова "ПРУДКІСТЬ" | Словник української мови. Словник Грінченка. hrinchenko.com. Процитовано 5 грудня 2022.
- ↑ Що таке БИСТРОТА - Українсько-російський словник - Словники - Словопедія. slovopedia.org.ua. Процитовано 5 грудня 2022.
- ↑ Яворский Б. М., Пинский А. А. Основы физики. — М. : Физматлит, 2003. — Т. 1. — 576 с.
- ↑ Четаев Н. Г. Теоретическая механика. — М. : Наука, 1987. — 368 с.
- ↑ ДСТУ 3651.2-97 Метрологія. Одиниці фізичних величин. Фізичні сталі та характеристичні числа. Основні положення, позначення, назви та значення.
- ↑ Resolution 1 of the 17th CGPM. BIPM. 1983. Архів оригіналу за 23 червня 2013. Процитовано 23 серпня 2009.
Джерела[ред. | ред. код]
- Єжов С. М., Макарець М. В., Романенко О. В. Класична механіка. — К. : ВПЦ "Київський університет", 2008. — 480 с.
- Федорченко А. М. Теоретична механіка. — К. : Вища школа, 1975. — 516 с.
- Дідух Л. Д. Основи механіки. — Тернопіль : Підручники і посібники, 2010. — 304 с. — ISBN 978-966-07-1817-3.
- Вайданич В. І., Пенцак Г. М. Фізика. — Львів : Національний лісотехнічний університет України, 2009. — 664 с. — ISBN 5-7763-0227-7.
- Воловик П. М. Фізика для університетів. — Київ : Перун, 2011. — 864 с. — ISBN 966-569-172-4.
- Іванків Я. І., Палюх Б. М. Механіка [Текст] : навч. посібник для студ. фіз. спец. вузів. — Київ : ІСДО, 1995. — 228 с. — ISBN 5-7763-9897-5.
- Козицький С. В., Поліщук Д. І. Курс загальної фізики: підруч. для студ. ВНЗ: у 6 т. Т. 1. Механіка. — Одеса : Астропринт, 2011. — 471 с.
- Методи та засоби вимірювання вихрового компонента швидкості течії: монографія / В. Д. Погребенник ; М-во освіти і науки України, Нац. ун-т «Львів. політехніка». — Львів: Вид-во Львів. політехніки, 2015. — 180 с. : іл. — Режим доступу: . — Бібліогр.: с. 171—178 (123 назви). — ISBN 978-617-607-768-8
Посилання[ред. | ред. код]
- Швидкість // Термінологічний словник-довідник з будівництва та архітектури / Р. А. Шмиг, В. М. Боярчук, І. М. Добрянський, В. М. Барабаш ; за заг. ред. Р. А. Шмига. — Львів, 2010. — С. 213. — ISBN 978-966-7407-83-4.
- «Швидкість» [Архівовано 15 грудня 2013 у Wayback Machine.] в Академічному тлумачному словнику української мови в 11 томах. Т. 11, С. 430.
- Швидкість [Архівовано 4 березня 2016 у Wayback Machine.] // Українська радянська енциклопедія : у 12 т. / гол. ред. М. П. Бажан ; редкол.: О. К. Антонов та ін. — 2-ге вид. — К. : Головна редакція УРЕ, 1974–1985..
|
|




















































































