Тертя кочення



Тертя́ ко́чення — опір рухові, що виникає при перекочуванні тіла одне по одному. За ДСТУ 2823-94[1] тертя кочення — тертя руху, під час якого швидкості тіл однакові за величиною і напрямком, принаймні, в одній точці зони контакту. Проявляється, наприклад, між елементами підшипників кочення, між шиною колеса автомобіля і дорожнім полотном. Як правило, зусилля тертя кочення набагато менші від зусиль тертя ковзання і тому, кочення є поширеним видом руху в техніці.
Тертя кочення виникає на межі двох тіл, і тому воно класифікується як вид зовнішнього тертя.
Динаміка тертя кочення[ред. | ред. код]
Сила тертя кочення[ред. | ред. код]
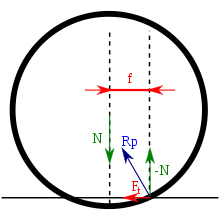
На тіло, що котиться по поверхні діють сили:
- P — тягнуча сила, що прикладена до середини тіла;
- N — сила притискування тіла до поверхні кочення;
- Rp — асиметрична сила реакції поверхні кочення.
Якщо векторна сума цих сил дорівнює нулю, то середина тіла кочення рухається рівномірно прямолінійно (див. рис.1).
Це означає що вертикальна складова сили реакції зрівноважується притискною силою, а горизонтальна складова зрівноважується тягнучою силою, протидіючи рухові тіла кочення і за аналогією до тертя ковзання називається силою тертя кочення: .
Рівномірне кочення означає, також, що сума моментів сил відносно довільної точки дорівнює нулю. З рівноваги моментів сил зображених на рис.2 і 3 відносно середини тіла кочення випливає:
Звідки випливає:
де:
- — сила тертя кочення;
- f — коефіцієнт тертя кочення, одиниці вимірювання метр;
- R — радіус тіла кочення;
- N — притискна сила тіла до поверхні.
Ця залежність підтверджується експериментально. Для малої швидкості кочення сила тертя кочення не залежить від цієї швидкості. Коли швидкість кочення досягає значень, коли швидкість утворення деформації стає порівняльною із швидкістю поширення деформації в матеріалі, тертя кочення різко зростає і навіть може перевищити тертя ковзання за аналогічних умов.
Момент сил тертя кочення[ред. | ред. код]
Визначимо для рухомого циліндра гальмівний момент обертального руху тіла. Якщо розглянути цей момент відносно центру обертового колеса (наприклад, колеса автомобіля) то він дорівнюватиме добутку гальмівного зусилля на осі на радіус колеса. Відносно точки контакту рухомого тіла з землею момент буде рівний добутку тягового зусилля, що врівноважує сили тертя, на радіус колеса (рис.2).
- .
З іншого боку, момент тертя дорівнює моменту притискної сили (N) на плече довжиною, що дорівнює коефіцієнту тертя кочення (f):
- ,
де
- — момент тертя в [Н]·[м];
- — радіус тіла кочення;
- — тягнуча сила;
- — сила тертя кочення;
- — коефіцієнт тертя кочення в [м].
Коефіцієнт тертя кочення[ред. | ред. код]
Із записаного вище рівняння випливає, що коефіцієнт тертя може бути визначений як відношення моменту тертя кочення () до притискної сили (N):
Графічна інтерпретація коефіцієнта тертя кочення f подана на рис.3. і рис.4.
Коефіцієнт тертя кочення має наступні фізичні інтерпретації:
- Якщо тіло знаходиться у спокої і тягнуча сила відсутня, сила реакції поверхні кочення лежить на тій же лінії, що і притискна сила. Коли тіло котиться, з умови рівноваги випливає, що перпендикулярна складова сили реакції поверхні кочення є паралельною до притискної сили і не збігається з нею. Коефіцієнт тертя кочення дорівнює відстані між прямими, вздовж яких діють притискна сила і нормальна до поверхні кочення складова сили реакції поверхні (рис. 4).
- Тіло, що котиться можна розглядати як тіло, що обертається навколо миттєвої осі обертання (рис.4 — точка прикладання вектора ), котра для ідеально твердих матеріалів є точкою, що лежить на прямій, котра проходить через центр кола і перпендикулярна до поверхні кочення. Для випадку реальних матеріалів, точка миттєвого центру обертання є зміщеною у напрямку кочення тіла а відстань рівну значенню коефіцієнта тертя кочення.
Орієнтовні значення коефіцієнта тертя для різних пар кочення.
| Тіло кочення | Поверхня кочення | Коефіцієнт тертя в мм |
|---|---|---|
| деревина м'яка | деревина м'яка | 1,5 |
| деревина м'яка | сталь | 0,8 |
| деревина тверда | деревина тверда | 0,8 |
| ебоніт | бетон | 10-20 |
| ебоніт | сталь | 7,7 |
| гума | бетон | 15-35 |
| загартована сталь | загартована сталь | 0,01 |
| полімер | сталь | 2 |
| сталь | асфальт | 6 |
| сталь | тротуарна плитка | 1,5 |
| сталь | сталь | 0,5 |
| залізо | деревина м'яка | 5,6 |
| залізо | граніт | 2,1 |
| залізо | залізо | 0,51 |
| чавунне литво | чавунне литво | 0,8 |
Див. також[ред. | ред. код]
Примітки[ред. | ред. код]
- ↑ ДСТУ 2823-94 Зносостійкість виробів тертя, зношування та мащення. Терміни та визначення.
Джерела[ред. | ред. код]
- Онищенко О. Г., Коробко Б. О., Ващенко К. М. Структура, кінематика та динаміка механізмів. ПолтНТУ, 2010. — 274 с. ISBN 978-966-616-078-5

















