Повний граф
Перейти до навігації
Перейти до пошуку
Повний граф — простий граф, в якому кожна пара різних вершин суміжна, тобто існує ребро, що сполучає ці вершини. Повний граф зазвичай позначається Kn.
Властивості[ред. | ред. код]
- Повний граф з n вершинами має n(n - 1)/ 2 ребер
- Повний граф з n вершинами є регулярним графом степеня n - 1.
- Графи K1 — K4 є планарними. Повні графи з більшою кількістю вершин не є планарними, оскільки містять підграф K5 і, отже, не задовольняють умови Куратовського.
- Повний граф є однозначно розфарбовуваним, оскільки існує лише одне допустиме розфарбування — кожній вершині призначається свій колір[1].
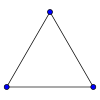
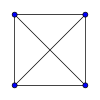
Нижче подані зображення повних графів з кількістю вершин від 1 до 11.

|

|
|
|

|

|

|

|

|

|

|
Див. також[ред. | ред. код]
Джерела[ред. | ред. код]
- Ф. Харари. Теория графов. М.: «Мир». 1973
- Р.Уилсон. Введение в теорию графов. М.: Мир, 1977
- ↑ Thomas Fowler. Unique Coloring of Planar Graphs. — Georgia Institute of Technology Mathematics Department, 1998. — (Ph.D. thesis)










