Планарний граф

Планарний граф — граф, який може бути зображений на площині без перетину ребер.

Граф зображений на площині називається плоским, якщо його ребра не перетинаються. Граф називається планарним, якщо він ізоморфний деякому плоскому графу. Тобто існує відображення вершин графа на деякі точки площини і ребер графа на прості криві у площині, так що кінцями кривих є точки, що відповідають вершинам ребра і дві різні криві не мають спільних точок, окрім можливо кінцевих.

Критерій непланарності

• достатня умова — якщо граф містить двочастковий підграф K_3,3 або повний підграф K₅, то він є не планарним;
• необхідна умова — якщо граф не планарний, то він повинен містити більше 4 вершин, степінь яких більше 3, або більше 5 вершин, степінь яких більше 2.

Теорема Куратовського

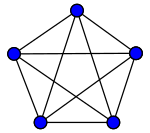
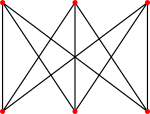
Граф є планарним тоді і тільки тоді, коли він не містить підграфів, гомеоморфних K₅ або K_3,3.

K₅, повний граф з 5 вершинами

K_3,3, повний двочастковий граф

Теорема Вагнера

Граф є планарним тоді і тільки тоді, коли він не містить підграфів, що стягуються в K₅ або K_3,3.

Формула Ейлера

Для зв'язного плоского графа справедливе таке співвідношення між кількістю вершин V, ребер E і граней F (включаючи зовнішню грань):

$V-E+F=2$

Його було знайдено Ейлером в 1736 році при вивченні властивостей опуклих багатогранників. Це співвідношення справедливе і для інших поверхонь з точністю до коефіцієнта, що називається характеристикою Ейлера. Це інваріант поверхні, для площини або сфери він дорівнює два.

Формула має багато корисних наслідків. З того, що кожна грань обмежена не менше ніж трьома ребрами і кожне ребро дотичне, щонайбільше до двох граней, випливає, що для плоского графа:

$E\leqslant 3V-6.$

Тобто, при більшому числі ребер граф непланарний. Звідси випливає, що в планарному графі завжди можна знайти вершину степеня не більше 5.

Властивості

• Довільний планарний граф може бути зображений на площині так, щоб всі його ребра були прямими відрізками (теорема Фарі).
• Вершини довільного планарного графа можна розфарбувати в чотири кольори так, щоб усі суміжні вершини мали різні кольори.

Різновиди планарних графів

Максимальні планарні графи

Граф Голднера — Харарі - максимальний планарний. Всі його грані обмежені трьома ребрами.

Граф називається максимальним планарним якщо він планарний, але додавання будь-якого ребра (до існуючих вершин) зробить його не планарним.

Зовнішні планарні графи

Граф K₄

Планарний граф називається зовнішнім планарним, якщо існує грань, що містить всі його вершини. Дані графи можна зобразити на поверхні так, що всі вершини будуть розміщені на колі.

Приклади

• Усі дерева є зовнішніми планарними графами.
• Граф K₄ є планарним графом, що не є зовнішнім планарним.

Властивості зовнішніх планарних графів

• Довільний зовнішній планарний граф має вершину степеня щонайбільше 2.
• Вершини довільного зовнішнього планарного графа можна розфарбувати в три кольори так, щоб усі суміжні вершини мали різні кольори.

Див. також

• Теорема про планарне розбиття
• Гіпотеза Шейнермана
• Теорема Шнайдера
• Критерій планарності Вітні

Джерела

1. А. Ю. Ольшанский. Плоские графы, СОЖ, 1996, No 11,
2. Ф. Харари. Теория графов. М.: «Мир». 1973