Зворотний перехід
Зворотний перехід (англ. backjumping) — одна з технік, що дозволяє зменшити простір пошуку у алгоритмах пошуку з поверненням, завдяки чому підвищується ефективність роботи. Суть методу полягає в тому, щоб повертатись не на один крок назад, як у бектрекінгу, а відразу на декілька.
-
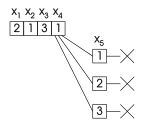
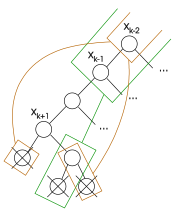
Обхід дерева пошуку алгоритмом з поверненням
-
Ілюстрація зворотного переходу: сірий вузол не відвідується
Визначення[ред. | ред. код]
Коли алгоритм пошуку з поверненням перебрав усі можливі значення змінної, він повертається до попередньої змінної і або надає їй наступного значення, або повертається ще вище. Інакше кажучи, якщо — поточна підстановка ( — змінна, — її значення) і алгоритм вже перебрав усі можливі значення для , то рішення, що починається з поточної підстановки, не існує. Після цього алгоритм переходить на рівень вище (де поточною підстановкою є ) і або змінює значення на наступне, або повертається ще на рівень вище.
Щоб довести, що при жодному значенні ми не досягнемо розв'язку, не обов'язково перебирати усі такі значення. Якщо алгоритм може довести, що існує індекс такий, що префікс ніяким чином не може бути доповнений до рішення, він може одразу перейти до зміни , не перебираючи піддерево поточної підстановки. Індекс , для якого алгоритм може довести вищезазначену властивість, називається «безпечним стрибком».
Ефективність алгоритму із зворотним переходом залежить від того, наскільки високо може перестрибнути алгоритм. Проте можливості алгоритму обмежені тим фактом, що в загальному випадку безпечність стрибка можна визначити лише виходячи з набору рішень. На практиці алгоритми зі зворотним переходом використовують найнижчий перехід, для якого безпечність може бути ефективно доведена.
Різні алгоритми визначають безпечність переходів по-різному, проте більш трудомісткі алгоритми визначення можуть окупатися за рахунок того, що більш високі переходи дозволяють економити час на переборі піддерев.
Зворотний перехід на листках дерева[ред. | ред. код]
Найпростішим випадком, в якому можливий зворотний перехід, є ситуація, коли усі можливі значення змінної є недопустимими. Наприклад, у задачі виконання обмежень поточна підстановка може задовольняти усім обмеженням, але може не існувати таких її розширень, що також задовольняють обмеженням. Така ситуація, коли усі значення змінної конфліктують із поточною підстановкою , а сама змінна є листком (тобто не має нащадків), називається «листовим глухим кутом».
Алгоритм із зворотним переходом за авторством Gaschnig робить перехід лише на листках. Інакше кажучи, він відрізняється від пошуку з поверненням лише тим, що може не перевіряти піддерева листків (тобто не перебирати усі можливі значення змінної ).
Безпечний перехід може бути знайдений визначенням для кожного значення найкоротшого префікса підстановки , що не сумісний з підстановкою . Інакше кажучи, якщо — допустиме значення змінної , то алгоритм має перевірити допустимість наступних підстановок:
| … | ||||
| … | ||||
| … | ||||
Найменший індекс, для якого знайдена несумісність, є безпечним стрибком для випадку, коли є єдиним допустимим значенням для . Оскільки зазвичай змінні можуть мати декілька допустимих значень, алгоритм виконує вищенаведені обрахунки для усіх, після чого із знайдений безпечних переходів обирається максимальний максимальний.
На практиці алгоритм може перевіряти вищенаведені умови одночасно із перевіркою підстановки .
Зворотний перехід на внутрішніх вузлах[ред. | ред. код]
Попередній алгоритм здійснює зворотний перехід лише тоді, коли для усіх допустимих значень змінної може бути доведено, що не існує розв'язків із поточною підстановкою. Іншими словами, він дозволяє робити перехід лише на листках дерева пошуку.
Внутрішній вузол представляє таке присвоювання значення, що не порушує уже існуючої відповідності обмеженням. Якщо не існує розв'язку, що розширює цю підстановку, попередній алгоритм завжди здійснює повернення на попередній крок, а не стрибок.
Для внутрішніх вузлів стрибок не може здійснюватись так само, як і для листків. Дійсно, якщо якісь присвоювання значень змінній потребують продовження пошуку у піддереві, отже, вони відповідають обмеженням, і не має сенсу шукати префікс, котрий ці обмеження порушує.
В таких випадках безперспективність присвоювання для поточної підстановки доводить рекурсивний пошук. Алгоритм «знає», що для даної підстановки не існує розв'язку, тому що він повертається у цю точку замість того, щоб знайти розв'язок і зупинитись.
Ці повернення зумовлені «глухими кутами», точками, в яких алгоритм довів несумісність підстановки із обмеженнями. Для того, щоб зробити стрибок, алгоритм має «зрозуміти», що рішення не вдається знайти саме через «глухі кути». Безпечними переходами будуть індекси префіксів, котрі перетворюють ці глухі кути у часткові підстановки, що не відповідають умовам.
Іншими словами, після перевірки усіх значень алгоритм може перейти до змінної за тієї умови, що поточна істинна підстановка несумісна із усіма істинними підстановками у листках візлів, що є нащадками .
Спрощення[ред. | ред. код]

Через потенційно велику кількість вузлів у піддереві змінної під час обробки цього піддерева збирається інфрмація, необхідна для безпечного стрибка із цієї змінної. Пошук безпечного стрибка може бути спрощений завдяки двом речам. Перше: хоча алгоритм і шукає безпечний стрибок, він не користується найвищим з можливих.
Друге можливе спрощення полягає у тому, що вузли піддерева змінної , що були пропущені стрибком, можуть бути проігноровані при пошуку стрибка для змінної . Точніше кажучи, вершини від до , що були пропущені стрибком, ніяк не пов'язані із піддеревом змінної і з іншими її піддеревами.
Дійсно, якщо алгоритм пішов від вершини до якимсь шляхом, але потім перестрибнув назад, він міг би просто перейти від до напряму. Таким чином, стрибок вказує на те, що вершини між та не мають відношення до піддерева вершини . Інакше кажучи, стрибок показує, що відвідування цієї частини дерева пошуку було помилкою. Завдяки цьому при пошуку стрибка із вершини або якогось з її предків ця частина дерева може бути проігнорована.

Цей факт може бути використаний наступним чином: у кожній вершині зберігатимемо перелік усіх змінних, яким вже присвоєні значення і котрих достатньо, щоб спростувати існування розв'язку у піддереві цієї вершини. Ці переліки складаються під час роботи алгоритму. При поверненні вище по дереву з переліку видаляється вершина, в якій він зберігався, після чого перелік переноситься у вершину, в яку виконується перехід. Переліки з вершин, котрі алгоритм перестрибує, автоматично ігноруються.
Зворотний перехід на графах[ред. | ред. код]
Суть зворотного переходу на графах полягає у тому, що безпечний стрибок може бути знайдений перевіркою того, які із змінних пов'язані із змінними , що представлені листовими вузлами. Кожна змінна (), що представлена листком і пов'язана із змінною , може бути використана для пошуку безпечних стрибків. Зокрема, коли всі значення змінної вже перебрані, ця множина містить індекси змінних, для яких не має змісту пробувати піддерево змінної . В результаті алгоритм може безпечно перестрибнути до найвищого індексу з цієї множини.
Той факт, що вершини, пропущені стрибком, можуть бути проігноровані, використовується наступним алгоритмом. Коли ми повертаємось із листового вузла, предку цього вузла (у випадку стрибка — вузлу, у який стрибаємо) відправляється множина змінних, що пов'язані із цим вузлом. Кожна внутрішня вершина підтримує таку саму множину. Кожного разу, коли вершина отримує множину від котрогось із своїх нащадків, отримана множина додається до вже існуючої у вузлі. Коли ми повертаємось чи стрибаємо із вузла, змінна вузла видаляється із множини, після чого множина відправляється у вершину, в котру здійснюється стрибок/перехід. Алгоритм працює завдяки тому, що у кожній вершині підтримується список змінних, котрого достатньо, щоб довести відсутність розв'язку у піддереві даного вузла. Так як множини відправляються лише коли ми покидаємо вузол, множини із вузлів, котрі ми перестрибуємо, просто ігноруються.
Зворотний перехід, що базується на конфліктах (або зворотний перехід, що управляється конфліктами)[ред. | ред. код]
conflict-based backjumping conflict-directed backjumping
Іще вишуканіший алгоритм, що у деяких випадках здатний досягти ще більших стрибків, заснований на перевірці не тільки присутності змінних у одній і тій самій умові, а й того, чи викликала ця умова несумісність. Зокрема, цей алгоритм зберігає одну з порушених умов у листових вузлах. У кожному вузлі найбільший індекс змінної, що бере участь в одній із умов, збережених у листках, є безпечним стрибком.
Хоча порушена умова у кожному листку не впливає на безпеку стрибка, вибір умови із найбільшим індексом підвищує «висоту» стрибка. Через це алгоритм із зворотним переходом, що управляється конфліктами, впорядковує умови таким чином, що обмеження для змінних із меншими індексами мають перевагу перед обмеженнями зі змінними із більшими індексами.
Формально кажучи, обмеження отримує перевагу перед обмеженням в тому випадку, коли найбільший індекс змінної у , але не в менший за найвищий індекс змінної у , але не в . Іншими словами, після виключення спільних змінних перевага надається обмеженню із найменшими індексами.
У листовому вузлі алгоритм надає перевагу індексу такому, що вступає у протиріччя із останньою змінною, що була обчислена у вузлі. Серед обмежень, що були порушені при цьому обчисленні, алгоритм обирає найвигіднішу (критерії див. вище), після чого вибирає усі індекси, що менші за . Таким чином, коли алгоритм приходить до змінної , найменший знайдений індекс є безпечним стрибком.
На практиці цей алгоритм спрощується завдяки збору усіх індексів у єдину множину замість створення множини для кожного значення . Зокрема алгоритм збирає у кожній вершині усі множини, що приходять від нащадків (як і раніше, лише від тих, що не були пропущені під час стрибку). При поверненні із вузла із множини видаляється змінна, що відповідає вузлу, після чого множина відправляється у точку стрибку/переходу.
Алгоритм із зворотним переходом, що управляється конфліктами, був запропонований для задачі виконання обмежень Патріком Просером у 1993-у році.
| На цю статтю не посилаються інші статті Вікіпедії. Будь ласка розставте посилання відповідно до прийнятих рекомендацій. |