Користувач:Anna Chopuk/Чернетка

Задачі теорії решіток — це клас задач оптимізації на ґратах (тобто дискретних адитивних підгрупах, заданих на множині $\mathbb {R} ^{n}$) .Гіпотетична погана можливість розв'язання таких задач є центральним місцем для побудови стійких криптосистем на ґратах. Для додатків в таких криптосистемах зазвичай розглядаються решітки на векторних просторах (часто $\mathbb {Q} ^{n}$) або вільних модулях (часто $\mathbb {Z} ^{n}$).

Для всіх задач нижче припустимо, що нам дано (крім інших більш конкретних вхідних даних) базис для векторного простору V і норма N. Для норм зазвичай розглядається L². Однак інші норми, такі як L^p), також розглядаються і з'являються в різних результатах . Нижче в статті $\lambda (L)$ означає довжину найкоротшого вектора в решітці L, тобто : $\lambda (L)=\min _{v\in L\setminus \{\mathbf {0} \}}\|v\|_{N}.$

Задачі знаходження найкоротшого вектора (ЗНВ)

Ілюстрація задачі знаходження найкоротшого вектора (основні(базові) вектори — синій колір, коротший вектор — червоний колір).

У ЗНВ (англ. Shortest vector problem, SVP), для решітки L дані базис векторного простору V і норма N (часто L²) і потрібно знайти ненульовий вектор мінімальної довжини в V за нормою N в решітці L. Іншими словами, виходом алгоритму повинен бути ненульовий вектор v, такий, що  $N(v)=\lambda (L)$.

В $\gamma$-наближеній версії ЗНВ_γ потрібно найти ненульовий вектор решітки довжини, що не перевищує $\gamma \lambda (L)$.

Труднощі

Тільки точна версія завдання, як відомо, є NP-важкою для рандомізованого відомості .

Для контрасту, відомо, що еквівалентна задача для рівномірних норм, є NP-важкою .

Алгоритми для евклідових норм

Для вирішення точної версії ЗНВ для евклідової норми відомі кілька різних підходів, які можна розбити на два класи — алгоритми, що вимагають суперекспоненціального часу ($2^{\omega (n)}$) і $\operatorname {poly} (n)$ пам'яті, і алгоритми, що вимагають експоненціального часу і пам'яті ($2^{\Theta (n)}$), від розмірності решітки($2^{\Theta (n)}$). У першому класі алгоритмів найбільш значимі алгоритми перерахування решітки і алгоритми скорочення випадкових вибірок , в той час як другий клас включає ґраткову просіювання , обчислення осередків Вороного на решітці і дискретні гаусові розподілу . Відкритою проблемою є, чи існують алгоритми, вирішальні точну ЗНВ за звичайне експоненціальне час ($2^{O(n)}$) і вимагають пам'яті, полІномІально залежить від розмірності решітки .

Для вирішення $\gamma$-наближеною версії ЗНВ_γ для $\gamma >1$ для евклідової норми кращий відомий підхід базується на використанні редукції базису решітки. Для великих $\gamma =2^{\Omega (n)}$ алгоритм Ленстра — Ленстра — Ловаш редукції базису решітки може знайти рішення за полІномІальний час від розмірності решітки. Для малих значень $\gamma$ зазвичай використовується блоковий алгоритм Коркіна — Золотарьова (БКЗ, англ. Block Korkine-Zolotarev algorithm, BKZ), де вхід алгоритму (розмір блоку $\beta$) визначає часову складність і якість виходу — для великих аппроксимаціонних коефіцієнтам $\gamma$ достатній малий розмір блоку $\beta$ і алгоритм завершується швидко. Для малих $\gamma$ вимагається більший $\beta$, щоб знайти досить короткі вектора решітки, і алгоритм працює довше. БКЗ-алгоритм всередині використовує алгоритм точного ЗНВ як підпрограми (працює на решітці розмірності, не перевершує $\beta$), і загальна складність тісно пов'язана з вартістю цих викликів ЗНВ в розмірності $\beta$.

GapSVP

Завдання $GapSVP_{\beta }$ полягає в розрізненні між варіантами ЗНВ, в яких відповідь не перевищує 1 або більше $\beta$ може бути фіксованою функцією від розмірності решітки $n$. Якщо заданий базис решітки, алгоритм повинен вирішити, буде $\lambda (L)\leqslant 1$ або $\lambda (L)>\beta$. Подібно до інших завданням з передумовою, алгоритму дозволені помилки у всіх інших випадках.

Іншою версією завдання є $GapSVP_{\zeta ,\gamma }$ для деяких функцій $\zeta ,\gamma$. Входом алгоритму є базис $B$ і число $d$. Алгоритм забезпечує, щоб всі вектора в ортогоналізації Грама — Шмідта мали довжину, не меншу 1, щоб $\lambda (L(B))\leqslant \zeta (n)$ і щоб $1\leqslant d\leqslant \zeta (n)/\gamma (n)$, де $n$ — розмірність. Алгоритм повинен прийняти, якщо $\lambda (L(B))\leqslant d$ і відкинути, якщо $\lambda (L(B))\geqslant \gamma (n).d$. Для великих $\zeta$ ($\zeta (n)>2^{n/2}$) завдання еквівалентна$GapSVP_{\gamma }$, оскільки препроцесорну крок за допомогою алгоритма ЛЛЛ робить друга умова (а отже, $\zeta$) зайвим.

Завдання знаходження найближчого вектору (ЗБВ)

Ілюстрація завдання знаходження найближчого вектору (базисні вектору показані синім кольором, найближчий вектор показаний червоним, зовнішній вектор показаний зеленим).

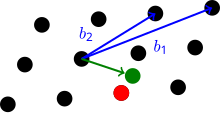
У ЗБВ (англ. Closest vector problem, CVP) для ґрат L дані бaзис векторного простору V і метрика M (часто L²), а також вектор v в V, але не обов'язково в L. Вимагається знайти вектор в L, найбільш близький до v (у міру M). У $\gamma$-приближеній версії ЗБВ_γ, треба знайти вектор ґрат на відстані, що не перевершує $\gamma$.

Зв'язок із ЗНВ

Завдання знаходження найближчого вектору є узагальненням завдання знаходження найкоротшого вектору. Легко показати, що якщо заданий провісник для ЗБВ_γ (визначений нижче)можна вирішити ЗНВ_γ шляхом деяких запитів провісникові. Природний метод пошуку найкоротшого вектору шляхом запитів до провісника ЗБВ_γ, щоб знайти найближчий вектор, не працює, оскільки 0 є вектором ґрат і алгоритм, потенційно, може повернути 0.

Зведення від ЗНВ_γ до ЗБВ_γ наступне: Припустимо, що входом завдання ЗНВ_γ являється базис ґрат $B=[b_{1},b_{2},\ldots ,b_{n}]$. Розглянемо базис $B^{i}=[b_{1},\ldots ,2b_{i},\ldots ,b_{n}]$ буде вектором, який повернув алгоритм ЗБВ$\gamma (B^{i},b_{i})$. Стверджується, що найкоротший вектор в множині $\{x_{i}-b_{i}\}$ являється найкоротшим вектором в даній решітці.

Труднощі

Голдрайх, Миссиансио, Сафра і Seifert показали, що з будь-якої складності ЗНВ витікає така ж складність для ЗБВ. Використовуючи засоби Арора, Babai, що перевіряється, Stern, Sweedyk показали, що ЗБВ важка для апроксимації до множника $2^{\log ^{1-\epsilon }(n)}$, якщо тільки не $\operatorname {NP} \subseteq \operatorname {DTIME} (2^{poly(\log n)})$. Динур, Киндлер, Сафра посилили це, вказавши NP- трудність з $\epsilon =(\log \log n)^{c}$ для $c<1/2$.

Сферичне декодування

Алгоритм для ЗБВ, особливо варіант Фінці і Поста використовується, наприклад, для виявлення даних у безпровідних системах зв'язку з багатоканальним входом/багатоканальним виходом (MIMO) (для кодованих і розкодованих сигналів) . У цьому контексті він називається сферичним декодуванням.

Алгоритм був застосований в області цілочисельного дозволу неоднозначності фази такою, що несе GNSS (GPS). У цій області це називається LAMBDA- методом.

GapSVP

Це завдання подібне до завдання GapSVP. Для $gapcvp_{\beta }$, входом є базис ґрат і вектор $v$, а алгоритм повинен відповісти, яка з умов виконується * існує вектор ґрат, такий, що відстань між ним і $v$ не перевершує 1. * будь-який вектор ґрат знаходиться від $v$ на відстані, більшому $\beta$.

Відомі результати

Завдання тривіально міститься в класі NP для будь-якого коефіцієнта апроксимації.

Клаус Шнорр в 1987 показав, що алгоритми з детермінованим поліноміальним часом можуть вирішити завдання $\beta =2^{O(n(\log \log n)^{2}/\log n)}$.Айтаі, Кумар, Сивакумар показали, що імовірнісні алгоритми можуть отримати злегка більше кращий коефіцієнт апроксимації $\beta =2^{O(n\log \log n/\log n)}$.

У 1993 Банашчик показав, що $GapCVP_{n}$ міститься в $NP\cap coNP$. У 2000 Голдрайх і Голдвассер показали, що $\beta ={\sqrt {n/\log n}}$ поміщає завдання в класи як NP, так і coAM. У 2005 Ааронов і Реджев показали, що для деякої константи $c$ завдання з $\beta =c{\sqrt {n}}$ входить в $NP\cap coNP$.

Завдання про найкоротші незалежні вектори

Якщо дані ґрати L розмірності n, алгоритм повинен видати n лінійно незалежних векторів $v_{1},v_{2},\ldots ,v_{n}$, таких, що $\max \|v_{i}\|<\max _{B}\|b_{i}\|$, де права частина складається з усіх базисів $B=\{b_{1},\ldots ,b_{n}\}$ ґрати.

У $\gamma$-приближенній версії, якщо дані ґрати L розмірності n, алгоритм знаходить n лінійно незалежних векторів $v1,v2,\ldots ,v_{n}$ довжини $\max ||v_{i}||\leqslant \gamma \lambda _{n}(L)$, де $\lambda _{n}(L)$ являється $n$-м подальшим мінімумом $L$.

Декодування з обмеженою відстанню

Це завдання подібне ЗБВ. Якщо даний вектор, такий, що його відстань від ґрат не перевершує $\lambda (L)/2$, алгоритм повинен видати найближчий вектор ґрат.

Завдання покриття ґрат радіусами

Якщо даний базис для ґрат, алгоритм повинен знайти найбільшу відстань (чи, в деяких версіях, його апроксимацію) від будь-якого вектору до ґрат.

Завдання пошуку найкоротшого базису

Багато завдань стають простіші, якщо вхідний базис складається з коротких векторів. Алгоритм, який вирішує задачу пошуку найкоротшого базису (ПКБ), повинен по заданому базису ґрат $B$ дати еквівалентний базис $B'$, такий, що довжина щонайдовшого вектору в $B'$ настільки коротка, наскільки можливо.

Апроксимована версія завдання ПКБ_γ полягає в пошуку базису, щонайдовший вектор якого не перевершує по довжині в $\gamma$ раз щонайдовшого вектору в найкоротшому базисі.

Використання в криптографії

Трудність середнього випадку завдань утворює базис для доказу стійкості більшості криптографічних схем. Проте експериментальні дані наштовхують на припущення, що для більшості NP- важких завдань ця властивість відсутня — вони лише важкі у гіршому разі. Для багатьох завдань теорії ґрат припустило або доведено, що вони важкі в середньому, що робить їх привабливими для криптографічних схем. Проте трудність у гіршому разі деяких завдань теорії ґрат використовується для створення схем стійкої криптографії. Використання трудності у гіршому разі в таких схемах поміщає їх в клас дуже небагатьох схем, які, з великою часткою вірогідності, стійкі навіть для квантових комп'ютерів.

Наведені вище завдання теорії ґрат легко вирішуються, якщо даний «хороший» базис. Мету алгоритмів редукції базису по цьому базису ґрат видати новий базис, що полягає їх відносно коротких майже ортогональних векторів. Алгоритм Ленстри — Ленстри — Ловаша редукції базису ґрат був раннім ефективним алгоритмом для цього завдання, який може видати зредукований базис ґрат за поліноміальний час Цей алгоритм і його подальші поліпшення були використані для злому деяких криптографічних схем, що сформувало його статус як дуже важливий засіб в криптографії. Успіх ЛЛЛ на експериментальних даних привів до віри, що редукція базису ґрат на практиці може бути простим завданням. Проте ця віра була зруйнована, коли у кінці 1990s-х були отримані нові результати про трудність завдань теорії ґрат, починаючи з результатівАйтаі. У своїй засадничій роботіАйтаі показав, що ЗНВ був NP- важким і виявив деякі зв'язки між складністю у гіршому разі і складністю в середньому деяких завдань теорії ґрат. Грунтуючись на цих результатах, Айтаі і Дворк створили криптосистему з відкритим ключем, секретність якої може бути доведена, використовуючи лише гірший випадок трудності певної версії ЗНВ, що було першим результатом по створенню захищених систем з використанням трудності у гіршому разі.

См також

• Навчання з помилками

Література

• Subhash Khot. Hardness of approximating the shortest vector problem in lattices // J. ACM. — 2005. — Т. 52, вип. 5. — DOI:10.1145/1089023.1089027.

• Miklós Ajtai. The shortest vector problem in L₂ is NP- hard for randomized reductions // Proceedings of the thirtieth annual ACM symposium on Theory of computing. — Dallas, Texas, United States : ACM, 1998.

• Peter van Emde Boas. Another NP - complete problem and the complexity of computing short vectors in a lattice. — University of Amsterdam, Department of Mathematics, Netherlands, 1981.

• Chris Peikert. Public - key cryptosystems from the worst - case shortest vector problem: extended abstract // Proceedings of the 41st annual ACM symposium on Theory of Computing. — Bethesda, MD, USA : ACM, 2009.
• Daniele Micciancio, Shafi Goldwasser. Complexity of Lattice Problems : A Cryptographic Perspective. — 2002. — Т. 671. — (Kluwer International Series in Engineering and Computer Science) — ISBN 0792376889.

• Daniele Micciancio, Shafi Goldwasser. Complexity of Lattice Problems : A Cryptographic Perspective. — Springer US, 2011. — (The Springer International Series in Engineering and Computer Science) — ISBN 9781461508984.

• Goldreich O., Micciancio D., Safra S., Seifert J. - p. Approximating shortest lattice vectors is not harder than approximating closest lattice vectors // Inf. Process. Lett.. — 1999. — Т. 71, вип. 2. — DOI:10.1016/S0020 - 0190 (99) 00083-6.

• Oded Goldreich, Shafi Goldwasser. On the limits of non - approximability of lattice problems // Proceedings of the thirtieth annual ACM symposium on Theory of computing. — Dallas, Texas, United States : ACM, 1998.

• Sanjeev Arora, László Babai, Jacques Stern, Z. Sweedyk. The hardness of approximate optima in lattices, codes, and systems of linear equations // J. Comput. Syst. Sci.. — 1997. — Т. 54, вип. 2. — DOI:10.1109/SFCS.1993.366815.

• Dinur I., Kindler G., Safra S. Approximating CVP to Within Almost - Polynomial Factors is NP - Hard // Combinatorica. — 2003. — Т. 23, вип. 2. — DOI:10.1007/s00493 - 003-0019 - y.

• Dinur I., Kindler G., Safra S. Approximating - CVP to within Almost - Polynomial Factors is NP - Hard // Proceedings of the 39th Annual Symposium on Foundations of Computer Science. — IEEE Computer Society, 1998. — ISBN 0-8186-9172-7.

• Fincke U., Pohst M. Improved Methods for Calculating Vectors of Short Length in a Lattice, Including a Complexity Analysis // Math. Comp.. — 1985. — Т. 44, вип. 170. — DOI:10.1090/S0025 - 5718-1985-0777278-8.

• Biglieri E., Calderbank R., Constantinides A., Goldsmith A., Paulraj A., Poor H. V. MIMO Wireless Communications. — Cambridge : Cambridge U. P, 2007.

• Ping Wang, Tho Le - Ngoc. A List Sphere Decoding Algorithm with Improved Radius Setting Strategies // Wireless Personal Communications. — 2011. — Т. 61, вип. 1. — DOI:10.1007/s11277 - 010-0018-4.

• Hassibi A., Boyd S. Integer Parameter Estimation in Linear Models with Applications to GPS // IEEE Trans. Sig. Proc.. — 1998. — Т. 46, вип. 11. — DOI:10.1109/78.726808.

• Miklós Ajtai, Ravi Kumar, D. Sivakumar. A sieve algorithm for the shortest lattice vector problem // Proceedings of the thirty - third annual ACM symposium on Theory of computing. — Hersonissos, Greece : ACM, 2001.

• Banaszczyk W. New bounds in some transference theorems in the geometry of numbers // Math. Ann.. — 1993. — Т. 296, вип. 1. — DOI:10.1007/BF01445125.

• Dorit Aharonov, Oded Regev. Lattice problems in NP $\cap$ coNP // J. ACM. — 2005. — Т. 52, вип. 5. — DOI:10.1145/1089023.1089025.

• Ajtai M. Generating hard instances of lattice problems // Proceedings of the twenty - eighth annual ACM symposium on Theory of computing. — Philadelphia, Pennsylvania, United States : ACM, 1996.

• Miklós Ajtai, Cynthia Dwork. A public - key cryptosystem with worst - case/average - case equivalence // Proceedings of the twenty - ninth annual ACM symposium on Theory of computing. — El Paso, Texas, United States : ACM, 1997.
• Jin - Yi Cai. The Complexity of Some Lattice Problems // Algorithmic Number Theory. — 2000. — Т. 1838. — DOI:10.1007/10722028 1.
• Lenstra A. K., Lenstra H. W., Lovász L. Factoring polynomials with rational coefficients // Math. Ann.. — 1982. — Т. 261, вип. 4. — DOI:10.1007/BF01457454.
• Daniele Micciancio, Panagiotis Voulgaris. Faster Exponential Time Algorithms for the Shortest Vector Problem // Proceedings of the Twenty - first Annual ACM - SIAM Symposium on Discrete Algorithms. — Philadelphia, PA, USA : Society for Industrial and Applied Mathematics, 2010. — С. 1468-1480. — (SODA '10) — ISBN 9780898716986.
• Daniele Micciancio, Panagiotis Voulgaris. A Deterministic Single Exponential Time Algorithm for Most Lattice Problems Based on Voronoi Cell Computations // Proceedings of the Forty - second ACM Symposium on Theory of Computing. — New York, NY, USA : ACM, 2010a. — ISBN 9781450300506. — DOI:10.1145/1806689.1806739.

• Becker A., Ducas L., Gama N., Laarhoven T. Proceedings of the Twenty - Seventh Annual ACM - SIAM Symposium on Discrete Algorithms. — Society for Industrial and Applied Mathematics, 2015. — С. 10-24. — (Proceedings) — DOI:10.1137/1.9781611974331.ch2.

• Divesh Aggarwal, Daniel Dadush, Oded Regev, Noah Stephens - Davidowitz. Solving the Shortest Vector Problem in 2n Time Using Discrete Gaussian Sampling : Extended Abstract // Proceedings of the Forty - seventh Annual ACM Symposium on Theory of Computing. — New York, NY, USA : ACM, 2015. — (STOC) — ISBN 9781450335362. — DOI:10.1145/2746539.2746606.

• Daniele Micciancio. Lattice Cryptography - Shortest Vector Problem. — 2017.

• Schnorr C. P. A hierarchy of polynomial time lattice basis reduction algorithms // Theoretical Computer Science. — 1987. — Т. 53, вип. 2. — DOI:10.1016/0304-3975 (87) 90064-8.

• Schnorr C. P., Euchner M. [https ://link.springer.com/article/10.1007/BF01581144 Lattice basis reduction: Improved practical algorithms and solving subset sum problems] // Mathematical Programming. — 1994. — Т. 66, вип. 1-3. — ISSN 0025-5610. — DOI:10.1007/bf01581144.
• Claus Peter Schnorr. Lattice Reduction by Random Sampling and Birthday Methods // [https ://link.springer.com/chapter/10.1007/3-540-36494-3 14 STACS]. — Springer, Berlin, Heidelberg, 2003. — ISBN 3540364943. — DOI:10.1007/3-540-36494-3 14.

• Schnorr C. P. Factoring integers and computing discrete logarithms via diophantine approximation // {{{Заголовок}}}. — 1993. — Т. 13. — С. 171-181. — (AMS DIMACS series in Disc. Math, and Theoretical Comp. Science)

• Yuanmi Chen, Phong Q. Nguyen. [https ://link.springer.com/chapter/10.1007/978-3-642-25385-0 1 Advances in Cryptology - ASIACRYPT 2011]. — Springer, Berlin, Heidelberg, 2011. — DOI:10.1007/978-3-642-25385-0 1.

Література для подальшого читання

• Agrell E., Eriksson T., Vardy A., Zeger K. Closest Point Search in Lattices // IEEE Trans. Inform. Theory. — 2002. — Т. 48, вип. 8. — DOI:10.1109/TIT.2002.800499.

• Daniele Micciancio. The Shortest Vector Problem is \u007BNP\u007D- hard to approximate to within some constant // SIAM Journal on Computing. — 2001. — Т. 30, вип. 6. — С. 2008-2035. — DOI:10.1137/S0097539700373039.

• Phong Q. Nguyen, Jacques Stern. Lattice Reduction in Cryptology : An Update // Proceedings of the 4th International Symposium on Algorithmic Number Theory. — Springer - Verlag, 2000. — С. 85-112. — ISBN 3-540-67695-3.

• Ravi Kannan. Improved Algorithms for Integer Programming and Related Lattice Problems // Proceedings of the Fifteenth Annual ACM Symposium on Theory of Computing. — New York, NY, USA : ACM, 1983. — (STOC) — ISBN 0897910990. — DOI:10.1145/800061.808749.
• Nicolas Gama, Phong Q. Nguyen, Oded Regev. Lattice Enumeration Using Extreme Pruning // [https ://link.springer.com/chapter/10.1007/978-3-642-13190-5 13 Advances in Cryptology - EUROCRYPT 2010]. — Springer, Berlin, Heidelberg, 2010. — DOI:10.1007/978-3-642-13190-5 13.
• Yoshinori Aono, Phong Q. Nguyen. Random Sampling Revisited : Lattice Enumeration with Discrete Pruning // [https ://link.springer.com/chapter/10.1007/978-3-319-56614-6 3 Advances in Cryptology - EUROCRYPT 2017]. — Springer, Cham, 2017. — DOI:10.1007/978-3-319-56614-6 3.
• Daniele Micciancio, Panagiotis Voulgaris. Faster Exponential Time Algorithms for the Shortest Vector Problem // [http: //dl.acm.org/citation.cfm? Id = 1873601.1873720 {{{Заголовок}}}]. — (SODA '10)
• Daniele Micciancio, Panagiotis Voulgaris. A Deterministic Single Exponential Time Algorithm for Most Lattice Problems Based on Voronoi Cell Computations // [http: //doi.acm.org/10.1145/1806689.1806739 {{{Заголовок}}}].
• Becker A., ​​Ducas L., Gama N., Laarhoven T. [http: //epubs.siam.org/doi/10.1137/1.9781611974331.ch2 {{{Заголовок}}}]. — (Proceedings)