Алгоритм сходження на вершину
Алгоритм пошуку зі сходженням до вершини (англ. Hill climbing) являє собою звичайний цикл, в якому постійно відбувається переміщення в напрямку зростання деякого значення, тобто підйом. Робота цього алгоритму закінчується після досягнення «піку», в якому жоден з сусідніх станів не має більш високого значення. У цьому алгоритмі не передбачено супровід дерева пошуку, тому в структурі даних поточного вузла необхідно реєструвати тільки стан і відповідне йому значення цільової функції.
В алгоритмі зі сходженням до вершини не здійснюється прогнозування за межами станів, які є безпосередньо сусідніми по відношенню до поточного стану. Це нагадує спробу альпініста, який страждає від амнезії, знайти вершину гори Еверест в густому тумані.
В інформатиці алгоритм сходження на вершину — це математичний метод оптимізації, який належить до сім'ї локального пошуку. Це ітераційний алгоритм, який починається з довільного розв'язку проблеми, а потім намагається знайти краще рішення, поступово змінючи один елемент розв'язку.
Наприклад, алгоритм сходження на вершину може бути застосований до задачі комівояжера. Легко знайти початкове значення, яке відвідує всі міста, але це буде дуже «бідним» в порівнянні з оптимальним рішенням. Алгоритм починається з таким рішенням і робить невеликі зміни до нього, такі, як зміна порядку відвідування двох міст. Зрештою, набагато коротший маршрут, ймовірно, буде отримано.
Алгоритм сходження на вершину хороший для знаходження локального оптимуму (рішення, яке не може бути поліпшене шляхом розгляду сусідніх конфігурацій), але знаходження оптимального розв'язку (глобальний оптимум) з усіх можливих рішень (простір пошуку) не гарантується.
Відносна простота алгоритму робить його популярним вибором серед алгоритмів оптимізації. Він широко використовується в галузі штучного інтелекту, для досягнення цільового стану від початкового вузла. Пов'язані алгоритми вибирають наступні та початкові вузли по-різному. Незважаючи на більш просунуті алгоритми, такі як імітація відпалу або табу-пошук, які можуть дати кращі результати, в деяких ситуаціях алгоритм сходження на вершину працює так само добре. Алгоритм сходження на вершину часто дає кращий результат, ніж інші алгоритми, коли кількість часу для виконання пошуку обмежена, наприклад, у системах реального часу.
Алгоритм сходження на вершину максимізує (або мінімізує) цільову функцію , де це вектор безперервного і / або дискретного значення. На кожній ітерації алгоритм сходження на вершину буде регулювати один елемент в і визначає, чи підвищує значення . (Зауважимо, що це відрізняється від методів градієнтного спуску, які регулюють всі значення в на кожній ітерації відповідно до градієнту пагорба.) Сходження на вершину приймає будь-яку зміну, яка поліпшує і процес триває допоки не буде знайдено значення в якому неможливо поліплишити Тоді оголошують локальним оптимальним розв'яком.
У дискретних векторних просторах, кожне можливе значення для можна собі уявити як вершину в графі.

У спрощеному алгоритмі сходження на вершину, обирають перший ближчий до розв'язку вузол, тоді як у найстрімкішому сходжені всі наступники порівнюються з обраним і тоді вибирається найближчий до розв'язку. Обидва варіанти можуть зазнати невдачі, якщо немає ближчого вузла, це може статись, якщо в області пошуку є локальні максимуми не розв'язки.
Стохастичний алгоритм сходження на вершину не розглядає всіх сусідів, перш ніж вирішити, як рухатися. Він радше обирає сусіда навмання і вирішує (спираючись на розмір поліпшення у цьому сусіді) чи вибрати цього сусіда чи перевірити іншого.
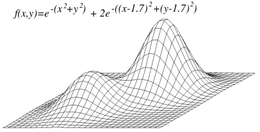
Локальний максимум являє собою пік, вищий в порівнянні з кожним з його сусідніх станів, але нижчий, ніж глобальний максимум. Алгоритми зі сходженням до вершини, які досягають околиць локального максимуму, забезпечують просування вгору, до цього піку, але після цього заходять в глухий кут, з якого більше нікуди рухатися.
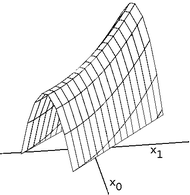
Приклад хребта зображений на малюнку. При наявності хребтів виникають послідовності локальних максимумів, завдача проходження яких для жадібних алгоритмів є дуже важкою через те, що кожен крок робить рух лише уздовж координатних осей. Якщо цільова функція утворює вузький хребет, що зростає не уздовж якоїсь з осей тоді алгоритм сходження може рухатись лише зігзагами. Якщо хребет надто вузький, то кроки будуть дуже маленькими і час на підйом може бути неприйнятно великим (або спуск, якщо шукаємо мінімум і маємо справу з улоговиною).
Це область в ландшафті простору станів, в якій функція оцінки є плоскою. Воно може являти собою плоский локальний максимум, з якого не існує виходу вгору, або уступ, з якого можливе подальше успішне просування. Пошук зі сходженням до вершини може виявитися нездатним вийти за межі плато.
Discrete Space Hill Climbing Algorithm
currentNode = startNode;
loop do
L = NEIGHBORS(currentNode);
nextEval = -INF;
nextNode = NULL;
for all x in L
if (EVAL(x) > nextEval)
nextNode = x;
nextEval = EVAL(x);
if nextEval <= EVAL(currentNode)
return currentNode;
currentNode = nextNode;
Continuous Space Hill Climbing Algorithm
currentPoint = initialPoint;
stepSize = initialStepSizes;
acceleration = someAcceleration;
candidate[0] = -acceleration;
candidate[1] = -1 / acceleration;
candidate[2] = 0;
candidate[3] = 1 / acceleration;
candidate[4] = acceleration;
loop do
before = EVAL(currentPoint);
for each element i in currentPoint do
best = -1;
bestScore = -INF;
for j from 0 to 4
currentPoint[i] = currentPoint[i] + stepSize[i] * candidate[j];
temp = EVAL(currentPoint);
currentPoint[i] = currentPoint[i] - stepSize[i] * candidate[j];
if(temp > bestScore)
bestScore = temp;
best = j;
if candidate[best] is not 0
currentPoint[i] = currentPoint[i] + stepSize[i] * candidate[best];
stepSize[i] = stepSize[i] * candidate[best];
if (EVAL(currentPoint) - before) < epsilon
return currentPoint;
- Hill Climbing visualization [Архівовано 30 серпня 2009 у Wayback Machine.] Візуалізація алгоритму сходження на вершину для задачі «N-Queens puzzle», зроблена Yuval Baror.


