Задача про мишей


У математиці задачею про мишей є задача, в якій декілька мишей (або комах, собак, ракет і т. д.), перебувають в кутах правильного многокутника. Кожна миша починає рухатися у напрямку до найближчого сусіда (за годинниковою стрілкою або проти годинникової стрілки). Рішенням цієї задачі є момент зустрічі мишей.
Найбільш поширений варіант задачі — коли миші починають рухатись з кутів одиничного квадрата, рухаючись з однаковою швидкістю. У цьому випадку вони зустрічаються через однаковий час, оскільки відстань між двома сусідніми мишами завжди зменшується, a швидкість стала. В цілому, для правильного багатокутника з n сторонами, відстань між сусідніми мишами зменшується зі швидкістю 1 − cos(2π/n), так що вони зустрінуться за час 1/(1 − cos(2π/n)).[1] [2]
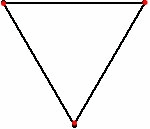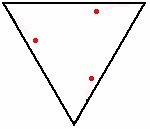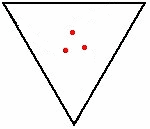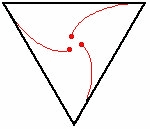
Для всіх правильних багатокутників, миші рухаються по логарифмічній спіралі, яка збігається в центрі багатокутника (як показано справа).[3] При додаванні мишей та якщо миші рухаються в напрямку не до безпосередніх сусідів, простежити їх шляхи більш складно.


- ↑ Гамов Георгій Антонович, Штерн, Марвін (1958), Математична головоломка, Нью Йорк: Viking press, с. 112–114
- ↑ Едвард Лукас, (1877), «Задача про трьох собак», Nouv. Corresp. Math. 3: с. 175–176
- ↑ Задача про мишей. MathWorld. Архів оригіналу за 13 квітня 2015. Процитовано 7 квітня 2015.
- Манія переслідування [Архівовано 19 квітня 2015 у Wayback Machine.] — Розширення задачі про мишей
| Це незавершена стаття з геометрії. Ви можете допомогти проєкту, виправивши або дописавши її. |