Мимобіжні прямі

Мимобіжні прямі

Дві прямі в тривимірному евклідовому просторі називаються мимобіжними, якщо не існує площини, що їх містить.

Відстань між двома мимобіжними прямими

Відстань між двома мимобіжними прямими

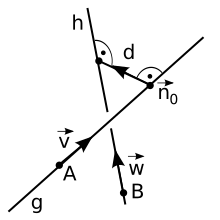
Відстанню між двома мимобіжними прямими називається довжина найкоротшого відрізка що їх з’єднує. Такий відрізок буде також перпендикуляром до обох прямих.

Позначимо напрямні вектори мимобіжних прямих як ${\vec {v}}$ і ${\vec {w}}$. Додатково виберемо три довільні точки А, В, О, так що A лежить на прямій g, B — на прямій h, а точка O не лежить на жодній з прямих і запишемо рівняння прямих в параметричній формі:

$g:{\vec {x}}={\vec {a}}+r{\vec {v}}$

$h:{\vec {x}}={\vec {b}}+s{\vec {w}}\ \ \,r,s\in \mathbb {R}$,

де ${\vec {a}},\,{\vec {b}},\,{\vec {v}},\,{\vec {w}}\in \mathbb {R} ^{3}$ .

Тоді напрям одиничної нормалі ${\vec {n}}$, до ${\vec {v}}$ і ${\vec {w}}$, а отже і до обох прямих, можна обчислити за допомогою векторного добутку:

${\vec {n}}_{0}={\frac {{\vec {v}}\times {\vec {w}}}{|{\vec {v}}\times {\vec {w}}|}}$.

Після чого відстань між прямими обчислюється як проєкція вектора ${\overrightarrow {OA}}$ на напрямок заданий одиничною нормаллю ${\vec {n}}_{0}$

$d(g,h)=|({\vec {a}}-{\vec {b}})\cdot {\vec {n}}_{0}|.$

Перевірка на мимобіжність

Якщо кожна пряма визначена за допомогою двох точок, через які вона проходить, тоді ці чотири точки мусять не бути колінеарними. Отже, вони мають бути вершинами чотиригранника з ненульовим об'ємом. І навпаки, будь-які дві двійки точок, що визначають чотиригранник не нульового об'єму, також визначають двійку мимобіжних прямих. З цього випливає, що перевірити на мимобіжність можна через застосування формули для знаходження об'єму чотиригранника, яка використовує його вершини. Позначаючи одну точку як 1×3 вектор a, три елементи якого є її координатами, і так само позначаючи інші три точки b, c і d, ми можемо перевірити, чи є мимобіжними пряма, що проходять через a і b і пряма, що проходить через c і d, порівнявши об'єм чотиригранника з нулем:

$V={\frac {1}{6}}\left|\det \left[{\begin{matrix}\mathbf {a} -\mathbf {b} \\\mathbf {b} -\mathbf {c} \\\mathbf {c} -\mathbf {d} \end{matrix}}\right]\right|.$

Див. Також

• Паралельні прямі

Посилання

Weisstein, Eric W. Мимобіжні прямі(англ.) на сайті Wolfram MathWorld.