Поворот дерева
Поворот дерева — операція над бінарним деревом, яка змінює його структуру без втручання в порядок елементів. Поворот дерева пересуває одну вершину вверх дерева і одну вниз. Використовується для зміни обрису дерева, особливо для зменшення висоти, пересуваючи менші піддерева вниз, а більші догори, в результаті покращення виконання багатьох операцій на дереві.
Домовленість, у який бік зсуваються вершини і є напрямком повороту.
Малюнок[ред. | ред. код]
Припустимо, що це бінарне дерево пошуку, тож інтерпретуємо елементи як змінні величини, а не як букви.
Деталізований малюнок[ред. | ред. код]
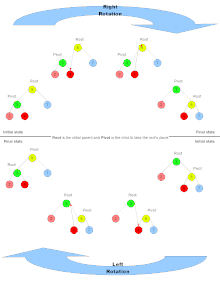
Коли піддерево повертається, тоді піддерево із сторони якого робиться поворот зменшує свою висоту на одиницю, а друге збільшує на одиницю. Це робить операцію корисною для збалансування дерев.
Використовувана термінологія — Root для кореневої вершини для повороту, Pivot для вершини, яка займе місце кореневої, RS для назви сторони з якої здійснюється поворот і OS для сторони протилежної повороту. Тоді можна записати такий псевдо-код повороту.
Pivot = Root.OS Root.OS = Pivot.RS Pivot.RS = Root Root = Pivot
Час такої операції не залежить від висоти дерева.
Програміст має також пересвідчитись, що вказівник на батьківську вершину для екскореневої вказує на вершину, що зайняла її місце. Також програміст має занотувати, що загальний корінь дерева може змінитися, тож треба бути обережним із вказівниками.
Поворот для балансування[ред. | ред. код]

Дерево може бути збалансоване використовуючи повороти. Після повороту, одна із сторін збільшує висоту на одиницю, у той час як інша зменшує. Отже, важливо використовувати повороти для вершин у яких висота лівого і правого піддерева різниться більше ніж на одиницю. Самозбалансовані дерева пошуку роблять це автоматично. АВЛ-дерево використовує таке збалансування.
Відстань обертання[ред. | ред. код]
Відстань обертання між будь-якими двома бінарними деревами з однаковою кількістю вершин — мінімальна кількість необхідних поворотів для перетворювання одного дерева в друге. З цією відстанню, набір n-вершинних дерев стає метричним простором: відстань обертання — симетрична, додаткова коли два дерева різні, і влаштовує нерівності трикутника.
Прорахунок відстані обертання— одна з відкритих проблем математики.
Посилання[ред. | ред. код]
- Java applets demonstrating tree rotations (dynamic)(англ.)
- Java applets demonstrating tree rotations(англ.)
- The AVL Tree Rotations Tutorial (RTF) by John Hargrove(англ.)
