Нерівність трикутника

Три приклади нерівності трикутника для трикутників зі сторонами з довжинами x, y, z. Верхній приклад показує випадок, коли z є значно меншою за суму інших двох сторін x + y, а нижній приклад показує випадок, коли сторона z є лише трошки меншою за x + y.

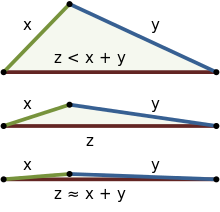
Нерівність трикутника — основна властивість геометричних фігур евклідового простору, відстані, що використовується в геометрії, функціональному аналізі.

Вона стверджує, що будь-яка сторона довільного трикутника менша за суму двох інших його сторін та більша за їх різницю.

Нерівність трикутника входить як аксіома в визначення метрики простору, норми.

Евклідова геометрія

Евклідова побудова доведення нерівності трикутника для планиметрії.

Нерівність трикутника є теоремою в Евклідовій геометрії, доведення наведено ще в «Началах» Евкліда.

В трикутнику $\ \Delta ABC:\;\;|AC|\leqslant |AB|+|BC|,$ причому рівність $\ |AC|=|AB|+|BC|$ досягається тільки тоді, коли трикутник вироджений і точка $B$ лежить строго між $A$ та $C$.

Нормований простір

Нерівність трикутника для норм векторів.

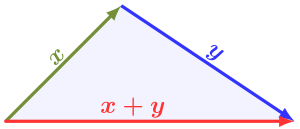
Якщо $(V,\|\cdot \|)$ — нормований векторний простір, де $V$ — довільна множина, а $\|\cdot \|$ — визначена на $V$ норма. Тоді за визначенням норми:

$\|x+y\|\leqslant \|x\|+\|y\|,\quad \forall x,y\in V.$

• В гільбертовім просторі, нерівність трикутника є безпосереднім єдинозворотнім нетривіальним наслідком нерівності Коші — Буняковского.

Метричний простір

Якщо $\ (X,\rho )$ — метричний простір, де $X$ — довільна множина, а $\ \rho$ — визначена на $X$ метрика. Тоді за визначенням метрики:

$\rho (x,y)\leqslant \rho (x,z)+\rho (z,y),\quad x,y,z\in X.$

Обернена нерівність трикутника

Наслідком нерівності трикутника в нормованому та метричному просторі є такі нерівності:

• ${\bigl |}\|x\|-\|y\|{\bigr |}\leqslant \|x-y\|,\quad x,y\in V;$
• $|\rho (x,y)-\rho (x,z)|\leqslant \rho (y,z),\quad x,y,z\in X.$

Джерела

• Э. Беккенбах, Р. Беллман (1965). Неравенства. Москва: Мир. {{cite book}}: Cite має пустий невідомий параметр: |1= (довідка)