Теорема про рівнобедрений трикутник

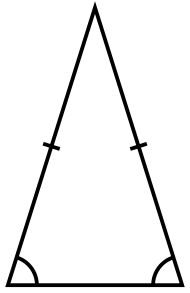
Теорема про рівнобедрений трикутник (англ. isosceles triangle theorem, або лат. Pons asinorum) — класична теорема геометрії, яка стверджує, що кути, протилежні бічним сторонам рівнобедреного трикутника, рівні. Ця теорема з'являється як пропозиція 5 книги 1 «Начал» Евкліда.

Справедливо і зворотне твердження: якщо два кути невиродженого трикутника рівні, то сторони, протилежні їм, є рівними. Теорема справедлива в абсолютній геометрії, а значить і в гіперболічній геометрії, вона виконується також у сферичної геометрії.

Pons asinorum

Креслення у доказі Евкліда

Диявольський міст

Ця теорема іноді називається лат. pons asinorum [ˈpons asiˈnoːrʊm] — «міст ослів».

Існують два можливих пояснення такої назви, одне полягає в тому, що креслення, яке використовується в доказі Евкліда нагадувало міст. Інше пояснення полягає в тому, що це перший серйозний доказ в «Началах» Евкліда — осли по ньому пройти не можуть.

Докази

Евкліда і Прокла

Евклід доводить додатково, що якщо бічні сторони трикутника продовжити за основу, то кути між продовженнями і основою теж рівні. Тобто, $\measuredangle CBF=\measuredangle BCG$ на кресленні до доказу Евкліда.

Прокл вказує на те, що Евклід ніколи не використовує це додаткове твердження і його доказ можна трохи спростити, провівши допоміжні відрізки до бічних сторонах трикутника, а не до їх продовженням. Інша частина доказу, проходить майже без змін. Прокл, припустив, що другий висновок може бути використаний як обґрунтування в доказі наступної пропозиції, де Евклід не розглянув усі випадки.

Доказ Прокла

Доказ спирається на попереднє припущення в «Началах» — на те, що сьогодні називають ознака рівності трикутників по двох сторонах і куту між ними.

Доказ Прокла

Нехай $\triangle ABC$ — рівнобедрений трикутник з рівними сторонами $AB$ і $AC$. Позначимо довільну точку $D$ на стороні $AB$ і побудуєм точку $E$ на стороні $AC$ так, щоб $AD=AE$. Проведемо відрізки $DC$, $BE$ і $DE$. Оскільки $AD=AE$, $AB=AC$ і кут $\angle A$ спільний, по рівності двох сторін і кута між ними, $\triangle BAE\cong \triangle CAD$, а отже рівні їх відповідні сторони і кути. Звідси кут $\measuredangle ABE=\measuredangle ACD$ і $\measuredangle AEB=\measuredangle ADC$ і $BE=CD$. Оскільки $AB=AC$ і $AD=AE$, віднімання з рівних частин рівні одержуєм $BD=CE$. Застосовуючи знов ознаку рівності трикутників по двох сторонах і куту між ними, одержуєм, що $\triangle DBE\cong \triangle ECD$. Звідси $\measuredangle BDE=\measuredangle CED$ і $\measuredangle BED=\measuredangle CDE$. Віднімаючи з рівних частин рівні одержуємо $\measuredangle BDC=\measuredangle CEB$. Знов таки за цією ознакою, одержуємо, що $\triangle BDC\cong \triangle CEB$. Отже $\measuredangle B=\measuredangle C$.

Папп

Прокл також наводить дуже короткий доказ, яке приписують Паппу. Він простіший і не вимагає додаткових побудов. У доказі застосовується ознака рівності по двох сторонах і куту між ними до трикутника і його дзеркального відображення.

Доказ Паппа

Нехай $\triangle ABC$ — рівнобедрений трикутник з рівними сторонами $AB$ і $AC$. Оскільки кут $\angle A$ спільний $AB=AC$ по двох сторонах і куту між ними $\triangle ABC\cong \triangle ACB$. Зокрема, $\measuredangle B=\measuredangle C$, що і треба було довести

Інші

Доказ Паппа іноді збиває учнів тим, що потрібно порівнювати трикутник «з самим собою». Тому, часто у підручниках дається наступне більш складне доведення. Воно простіше ніж доказ Евкліда, але використовує поняття бісектриси. В «Началах» побудова бісектриси кута наводиться тільки в реченні 9. Тому порядок викладу доводиться міняти, щоб уникнути можливості кругового міркування.

Доведення

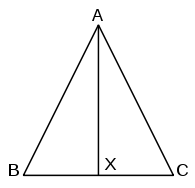
Нехай $\triangle ABC$ — рівнобедрений трикутник з рівними сторонами $AB$ і $AC$. Проведемо бісектрису кута $\angle A$. Нехай $X$ — точка перетину бісектриси з стороною $BC$. Відзначим, що $\triangle BAX\cong \triangle CAX$ оскільки $\measuredangle BAX=\measuredangle CAX$, $AB=AC$ і $AX$ спільна сторона. Отже, $\measuredangle B=\measuredangle C$, що і треба було довести.

Лежандр використовує подібні конструкції в своїх «Éléments de géométrie», но, приймаючи $X$ як середину $BC$. Доведення аналогічно, но використовується ознака рівності трикутників по трьох сторонах.

Див. також

• Начала Евкліда
• Теорема Аполлонія
• Теорема Штейнера — Лемуса