Алгоритм Шеннона — Фано
Алгоритм Шеннона — Фано — один з перших алгоритмів стиснення, який сформулювали американські вчені Шеннон і Фано. Даний метод стиснення має велику схожість з алгоритмом Хаффмана, який з'явився на кілька років пізніше. Алгоритм використовує коди змінної довжини: символ, який часто зустрічається, кодується кодом меншої довжини, а той що рідше зустрічається — кодом більшої довжини. Коди Шеннона — Фано префіксні, тобто ніяке кодове слово не є префіксом будь-якого іншого. Ця властивість дозволяє однозначно декодувати будь-яку послідовність кодових слів.
Основні відомості[ред. | ред. код]
Кодування Шеннона — Фано (англ. Shannon-Fano coding) — алгоритм префіксного неоднорідного кодування. Відноситься до ймовірнісних методів стиснення (точніше, методів контекстного моделювання нульового порядку). Подібно алгоритму Хаффмана, алгоритм Шеннона — Фано використовує надмірність повідомлення, укладених в неоднорідному розподілі частот його символів (первинного) алфавіту, тобто замінює коди символів, які частіше використовуються, короткими двійковими послідовностями, а коди більш рідкісних символів — більш довгими двійковими послідовностями.
Алгоритм був незалежно один від одного розроблений Шенноном (публікація «Математична теорія зв'язку», 1948 рік) і, пізніше, Фано (опубліковано як технічний звіт).
Основні етапи[ред. | ред. код]
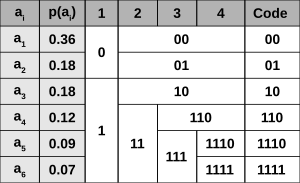
- Символи первинного алфавіту m1 виписують в порядку зменшення ймовірностей.
- Символи отриманого алфавіту ділять на дві частини, сумарні ймовірності символів яких максимально близькі один одному.
- У префіксному коді для першої частини алфавіту присвоюється двійкова цифра «0», другої частини — «1».
- Отримані частини рекурсивно діляться і їх частинам призначаються відповідні двійкові цифри в префіксному коді.
Коли розмір підалфавіту стає рівним нулю або одиниці, то наступне подовження префіксних коду для відповідних йому символів первинного алфавіту не відбувається, таким чином, алгоритм привласнює різним символам префіксні коди різної довжини. На кроці ділення алфавіту існує неоднозначність, так як різниця сумарних ймовірностей може бути однакова для двох варіантів поділу (враховуючи, що всі символи первинного алфавіту мають ймовірність більше нуля).
Алгоритм обчислення кодів Шеннона — Фано[ред. | ред. код]

Код Шеннона — Фано будується за допомогою дерева. Побудова цього дерева починається від кореня. Вся множина кодованих елементів відповідає кореню дерева (вершині першого рівня). Воно розбивається на дві підмножини з приблизно однаковими сумарними ймовірностями. Ці підмножини відповідають двом вершинам другого рівня, які з'єднуються з коренем. Далі кожна з цих підмножин розбивається на дві підмножини з приблизно однаковими сумарними ймовірностями. Їм відповідають вершини третього рівня. Якщо підмножина містить єдиний елемент, то йому відповідає кінцева вершина кодового дерева; така підмножина розбиттю не підлягає. Подібним чином поступаємо до тих пір, поки не отримаємо всі кінцеві вершини. Гілки кодового дерева розмічаємо символами 1 і 0, як у випадку коду Хаффмана.
При побудові коду Шеннона — Фано розбиття множини елементів може бути обрано, взагалі кажучи, декількома способами. Вибір розбиття на рівні n може погіршити варіанти розбиття на наступному рівні (n + 1) і призвести до неоптимальності коду в цілому. Іншими словами, оптимальна поведінка на кожному кроці шляху ще не гарантує оптимальності всієї сукупності дій. Тому код Шеннона — Фано не є оптимальним в загальному сенсі, хоча і дає оптимальні результати при деяких розподілах імовірностей. Для одного і того ж розподілу ймовірностей можна побудувати, взагалі кажучи, кілька кодів Шеннона — Фано, і всі вони можуть дати різні результати. Якщо побудувати всі можливі коди Шеннона — Фано для даного розподілу ймовірностей, то серед них будуть знаходитися і всі коди Хаффмана, тобто оптимальні коди.
Приклад кодового дерева[ред. | ред. код]
Вихідні символи:
- A (частота входження 50)
- B (частота входження 39)
- C (частота входження 18)
- D (частота входження 49)
- E (частота входження 35)
- F (частота входження 24)
| ABCDEF(215) | ||||||
|---|---|---|---|---|---|---|
| ABC(107) | DEF(108) | |||||
| A(50) | BC(57) | EF(59) | D(49) | |||
| B(39) | C(18) | E(35) | F(24) |
Отриманий код: A — 11, B — 101, C — 100, D — 00, E — 011, F — 010.
Кодування Шеннона —Фано є досить старим методом стиснення і на сьогоднішній день воно не представляє особливого практичного інтересу. У більшості випадків довжина послідовності, стиснутої за цим методом, дорівнює довжині стиснутої послідовності з використанням кодування Хаффмана. Але на деяких послідовностях можуть сформуватися неоптимальні коди Шеннона — Фано, тому більш ефективним вважається стиснення методом Хаффмана.
Література[ред. | ред. код]
- А. М. Яглом, И. М. Яглом. Вероятность и информация. — Издание третье, переработанное и дополненное. — Москва : Наука, 1973. — 512 с. (рос.)
- C. E. Shannon A Mathematical Theory of Communication [Архівовано 15 липня 1998 у Wayback Machine.] // Bell System Technical Journal. — № 27. — July 1948. — P. 379—423. (англ.)
- R. M. Fano The transmission of information // Technical Report. — № 65. — Cambridge (Mass., USA): Research Laboratory of Electronics at MIT, 1949. — P. 51. (англ.)
| Ця стаття потребує додаткових посилань на джерела для поліпшення її перевірності. (грудень 2015) |
| Це незавершена стаття про алгоритми. Ви можете допомогти проєкту, виправивши або дописавши її. |
| |||||||||||||||||||||||||||||||||||||||||||
