Граматика визначених тверджень
Грама́тика ви́значених тве́рджень (англ. Definite Clause Grammar (DCG), рос. DC-грамматика) — це спосіб представлення граматики природних або формальних мов у логічних мовах програмування, таких як Пролог. Він тісно пов’язаний з концепцією атрибутних граматик[en] / афіксних граматик[en], з якої Пролог і було спочатку розроблено. Граматики визначених тверджень зазвичай асоціюються із Прологом, але їх також включають і схожі мови, такі як Mercury[en]. Вони називаються граматиками визначених тверджень, оскільки представляють граматику множиною визначених тверджень у логіці першого порядку.
Термін «граматики визначених тверджень» відноситься до певного типу виразу в Пролозі та інших подібних мовах; не всі способи вираження граматик з використанням визначених тверджень вважаються граматиками визначених тверджень. Тим не менш, всі можливості та властивості граматик визначених тверджень будуть однаковими для будь-якої граматики, що представлена визначеними твердженнями, так само по суті, як і в Пролозі.
Визначені твердження таких граматик можуть розглядатися як набір аксіом, де справедливість вхідної стрічки, а також факт того, що вона має певне дерево синтаксичного аналізу, можуть розглядатися як теореми, що випливають з цих аксіом.[1] Це має таку перевагу, що розпізнавання та аналіз виразів у мові перетворюється на доведення тверджень, таких як твердження логічної мови програмування.
Історія[ред. | ред. код]
Історія граматик визначених тверджень тісно пов’язана з історією Прологу, а історія Прологу обертається навколо кількох дослідників у Марселі (Франція) та Единбурзі (Шотландія). Згідно з Робертом Ковальським, початковим розробником Прологу, першу прологову систему було розроблено у 1972 році Аланом Кольмерое[en] та Філіпом Русселем[fr].[2] Першою програмою, написаною цією мовою, була велика система обробки природної мови. До початкової розробки Прологу були також залучені Фернандо Перейра та Девід Воррен[en] з Единбурзького університету.
Кольмерое раніше працював над системою обробки мови, що називалася Q-systems, і яка використовувалася для перекладу між англійською та французькою.[3] У 1978-мому Кольмерое написав статтю про спосіб представлення граматик, що називався метаморфозними граматиками (англ. metamorphosis grammars), що були частиною ранньої версії Прологу, що називалася Марсельським прологом. У цій статті він дав формальний опис метаморфозних граматик і деякі приклади програм, що їх використовують.
Фернандо Перейра та Девід Воррен, двоє інших ранніх творців Прологу, створили термін «граматика визначених тверджень», і запис для них, що використовується в Пролозі й сьогодні. Вони віддали належне ідеї Кольмерое та Ковальського, і відзначили, що граматики визначених тверджень є окремим випадком метаморфозних граматик Кольмерое. Вони представили цю ідею у статті під назвою «Граматики визначених тверджень для мовного аналізу» (англ. «Definite Clause Grammars for Language Analysis»), де вони описали граматики визначених тверджень як «формалізм ... у якому граматики виражаються твердженнями логіки предикатів першого порядку», що «утворюють ефективні програми мови програмування Пролог».[4]
Пізніше Перейра, Воррен та інші піонери Прологу описали деякі інші аспекти граматик визначених тверджень. Перейра та Воррен написали статтю під назвою «Синтаксичний аналіз як дедукція» (англ. «Parsing as Deduction»), що описувала такі речі, як використання процедури доведення дедукція Ерлі для синтаксичного аналізу.[5] Перейра також працював разом зі Стюартом Шибером над книгою «Пролог та аналіз природних мов» (англ. «Prolog and Natural Language Analysis»), що призначалася для загального введення в обчислювальну лінгвістику з використанням логічного програмування.[6]
Приклад[ред. | ред. код]
Простий приклад граматик визначених тверджень для ілюстрації того, чим вони є, і як вони виглядають.
речення --> група_іменника, група_присудка.
група_іменника --> означення, іменник.
група_присудка --> дієслово, група_іменника.
означення --> [the].
означення --> [a].
іменник --> [cat].
іменник --> [bat].
дієслово --> [eats].
Ця граматика створює такі речення, як "the cat eats the bat", "a bat eats the cat". Можна згенерувати всі коректні речення мови, що генеруються цією граматикою, ввівши в інтерпретаторі Прологу речення(X,[]). Аналогічно, можна перевірити, чи є якесь речення коректним у цій мові, ввівши щось на кшталт речення([the,bat,eats,the,bat],[]).
Переклад визначеними твердженнями[ред. | ред. код]
Запис граматик визначених тверджень є лише синтаксичним цукром для звичайних визначених тверджень Прологу. Наприклад, попередній приклад можна перекласти так:
речення(S1,S3) :- група_іменника(S1,S2), група_присудка(S2,S3).
група_іменника(S1,S3) :- означення(S1,S2), іменник(S2,S3).
група_присудка(S1,S3) :- дієслово(S1,S2), група_іменника(S2,S3).
означення([the|X], X).
означення([a|X], X).
іменник([cat|X], X).
іменник([bat|X], X).
дієслово([eats|X], X).
Списки відмінностей[ред. | ред. код]
Аргументи кожного функтора, такі як (S1,S3) та (S1,S2), є списками відмінностей[en]; списки відмінностей є способом представлення списку як різниці двох списків. Використовуючи запис Прологу для списків, список L можна представити парою ([L|X],X).
Списки відмінностей використовуються для представлення списків у граматиках визначених тверджень з міркувань ефективності. Ефективніше конкатенувати списки відмінностей, в умовах, в яких вони можуть застосовуватися, оскільки конкатенацією (S1,S2) та (S2,S3) є просто (S1,S3).[7]
Не-контекстно-вільні граматики[ред. | ред. код]
У чистій Пролог звичайні правила граматик визначених тверджень без додаткових аргументів на функторах, як у попередньому прикладі, можуть виражати лише контекстно-вільні граматики; у лівій частині продукції[en] є лише один аргумент. Однак, контекстно-залежні граматики також можуть виражатися граматиками визначених тверджень шляхом надання додаткових аргументів, як у наступному прикладі:
s --> a(N), b(N), c(N).
a(0) --> [].
a(M) --> [a], a(N), {M is N + 1}.
b(0) --> [].
b(M) --> [b], b(N), {M is N + 1}.
c(0) --> [].
c(M) --> [c], c(N), {M is N + 1}.
Цей набір правил граматики визначених тверджень описує граматику, що генерує мову, що складається зі стрічок вигляду .[8]
s --> symbols(Sem,a), symbols(Sem,b), symbols(Sem,c).
symbols(end,_) --> [].
symbols(s(Sem),S) --> [S], symbols(Sem,S).
Цей набір правил граматики визначених тверджень описує граматику, що генерує мову, що складається зі стрічок вигляду , представляючи структурно.[джерело?]
Представлення словозмін[ред. | ред. код]
Деякі лінгвістичні словозміни також можуть досить чітко представлятися граматиками визначених тверджень шляхом додавання додаткових аргументів до функторів.[9] Наприклад, розгляньмо наступний набір правил граматики визначених тверджень:
речення --> іменник(називний_відмінок), група_присудка.
група_присудка --> дієслово, іменник(знахідний_відмінок).
іменник(називний_відмінок) --> [кіт].
іменник(називний_відмінок) --> [кажан].
іменник(знахідний_відмінок) --> [кота].
іменник(знахідний_відмінок) --> [кажана].
дієслово --> [їсть].
Ця граматика дозволяє такі речення як «кіт їсть кажана» та «кіт їсть кота», але не «кажана їсть кіт» та «кота їсть кота».
Синтаксичний аналіз із граматиками визначених тверджень[ред. | ред. код]
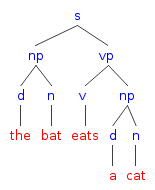
Головним практичним застосуванням граматик визначених тверджень є синтаксичний аналіз виразів заданої граматики, тобто, побудова дерева синтаксичного розбору. Це може бути реалізовано за допомогою застосування «додаткових аргументів» у функторах граматики визначених тверджень, як у наступних правилах:
речення(s(NP,VP)) --> група_іменника(NP), група_присудка(VP).
група_іменника(np(D,N)) --> означення(D), іменник(N).
група_присудка(vp(V,NP)) --> дієслово(V), група_іменника(NP).
означення(d(the)) --> [the].
означення(d(a)) --> [a].
іменник(n(bat)) --> [bat].
іменник(n(cat)) --> [cat].
дієслово(v(eats)) --> [eats].
Тепер можна зробити інтерпретаторові запит видати дерево розбору заданого речення:
| ?- речення(Синтаксичне_дерево, [the,bat,eats,a,cat], []).
Синтаксичне_дерево = s(np(d(the),n(bat)),vp(v(eats),np(d(a),n(cat)))) ? ;
Інші застосування[ред. | ред. код]
Граматики визначених тверджень можуть слугувати синтаксичним цукром для приховування деяких параметрів у коді і в інших застосуваннях, крім синтаксичного аналізу. В декларативно чистій мові програмування Mercury[en] введення/виведення мусить представлятися парою аргументів io.state. Запис граматик визначених тверджень може застосовуватися для того, щоби робити використання введення/виведення зручнішим,[10] хоча зазвичай віддають перевагу записові зі змінними стану.[джерело?]
Запис граматик визначених тверджень застосовується в Mercury для синтаксичного аналізу та подібних речей так само, як і в Пролозі.
Розширення[ред. | ред. код]
З тих пір, як Перейра та Воррен представили граматики визначених тверджень, було запропоновано декілька розширень. Сам Перейра запропонував розширення, назване екстрапозиційними граматиками (англ. extraposition grammars, XGs).[11] Цю формальну систему було представлено, зокрема, для спрощення вираження певних граматичних феноменів, таких як ліва екстрапозиція. Перейра писав, що «Різниця між правилами екстрапозиційних граматик та правилами граматик визначених тверджень тоді в тому, що ліва частина правила екстрапозиційної граматики може містити кілька символів.» Це спрощує вираження правил контекстно-залежних граматик.
Інше, новіше розширення, що зробили дослідники з корпорації NEC у 1995 році, було названо мультимодальними граматиками визначених тверджень (англ. Multi-Modal Definite Clause Grammars, MM-DCGs). Їхнє розширення призначалося для уможливлення розпізнавання та синтаксичного аналізу виразів, що містять не текстові частини, наприклад, зображення.[12]
У 1984 році було описано інше розширення, назване трансляційними граматиками визначених тверджень (англ. definite clause translation grammars, DCTGs).[13] Запис трансляційних граматик визначених тверджень дуже схожий на запис граматик визначених тверджень; основна відмінність полягає у використанні в правилах ::= замість -->. Його було розроблено для зручності маніпулювання граматичними атрибутами.[14] Перетворення трансляційних граматик визначених тверджень у звичайні твердження Прологу схоже на перетворення граматик визначених тверджень, але додається 3 аргументи замість 2.
Див. також[ред. | ред. код]
- Обробка природної мови
- Граматика з фразовою структурою[en]
- Ієрархія Чомскі
- Контекстно-вільна граматика
Примітки[ред. | ред. код]
- ↑ Johnson, M. (1994). Two ways of formalizing grammars. Linguistics and Philosophy. 17 (3): 221—240. doi:10.1007/BF00985036. (англ.)
- ↑ Kowalski, R. A. The early years of logic programming. (англ.)
- ↑ Colmerauer, A. (1978). Metamorphosis grammars. Natural Language Communication with Computers: 133—189. (англ.)
- ↑ Pereira, F.; D. Warren (1980). Definite clause grammars for language analysis. (англ.)
- ↑ Pereira, F. C. N.; D. H. D. Warren (1983). Parsing as deduction. Proceedings of the 21st annual meeting on Association for Computational Linguistics. Association for Computational Linguistics Morristown, NJ, USA. с. 137—144. (англ.)
- ↑ Pereira, F. C. N.; S. M. Shieber (2002). Prolog and natural-language analysis. Microtome Publishing. (англ.)
- ↑ Fleck, Arthur. Definite Clause Grammar Translation. Архів оригіналу за 1 грудня 2008. Процитовано 16 квітня 2009. (англ.)
- ↑ Fisher, J. R. Prolog Tutorial -- 7.1. Архів оригіналу за 23 серпня 2013. Процитовано 24 вересня 2012. (англ.)
- ↑ DCGs give us a Natural Notation for Features. Архів оригіналу за 25 травня 2011. Процитовано 21 квітня 2009. (англ.)
- ↑ Prolog to Mercury Transition Guide: Input/Output. Архів оригіналу за 14 березня 2017. Процитовано 26.03.2015. (англ.)
- ↑ Pereira, F. (1981). Extraposition grammars. Computational Linguistics. 7 (4): 243—256. (англ.)
- ↑ Shimazu, H.; Y. Takashima (1995). Multimodal definite clause grammar. Systems and Computers in Japan. 26 (3). (англ.)
- ↑ Abramson, H. (1984). Definite clause translation grammars. (англ.)
- ↑ Sperberg-McQueen, C. M. A brief introduction to definite clause grammars and definite clause translation grammars. Архів оригіналу за 1 травня 2009. Процитовано 21 квітня 2009. (англ.)
Посилання[ред. | ред. код]
- Обробка природної мови за допомогою Прологу [Архівовано 26 травня 2009 у Wayback Machine.] (англ.)
- Контекстно-вільні граматики та граматики визначених тверджень [Архівовано 16 лютого 2012 у Wayback Machine.] (англ.)
- Definite Clause Grammars for Language Analysis [Архівовано 14 листопада 2012 у Wayback Machine.] (англ.)

