Арбелос

Арбелос (сіра область)

Арбелос (грец. Άρβυλος — шевський ніж) — геометрична фігура, яка є областю на площині, котра обмежена трьома півколами, що знаходяться по одну сторону від деякої прямої, яка містить їх діаметри, та з'єднані по кутах, що розташовуються на цій прямій.

Найдавніше відоме посилання на цю фігуру знаходиться в книзі Лем Архімеда, де окремі з його математичних властивостей згадані в Припущеннях з 4 по 8.

Етимологія

Типовий ніж шевця, якому арбелос зобов'язаний своїм ім'ям

Назва «арбелос», використана Архімедом, походить з грецького «ἡἄρβηλο» або «ἄρβυλο», що має значення «шевський ніж» — ніж, який використовується шевцями з античних часів по наші дні, форма леза якого нагадує цю геометричну фігуру.

Властивості

Два півкола обов'язково є вігнутими, з довільними діаметрів А і В; третє півколо опукле, з діаметром A + B.

Деякі спеціальні точки арбелосу

У наступних розділах кути арбелосу помічені $A$, $B$, $C$, таким чином, що діаметр зовнішнього півкола $BC$ має одиничну довжину; а діаметри внутрішніх напівкіл $AB$ і $AC$ мають довжину r і 1-r, відповідно. Буква $H$ позначає точку, де зовнішнє півколо перетинає лінію, яка перпендикулярна до діаметра через точку $A$.

Площа

Площа арбелосу еквівалентна площі кола з діаметром $HA$.

Доведення

Якщо BC = 1 та BA = r, тоді

• З трикутника BHA: $r^{2}+h^{2}=x^{2}$
• З трикутника CHA: $(1-r)^{2}+h^{2}=y^{2}$
• З трикутника BHC: $x^{2}+y^{2}=1$

За допомогою підстановки $y^{2}=(1-r)^{2}+x^{2}-r^{2}$. Розкриваючи дужки: $y^{2}=1-2r+x^{2}$. Підстановкою $y^{2}$ в рівняння трикутника BHC знаходимо $x$:

$x={\sqrt {r}}$

Підставляючи це, знаходимо рішення для $y$ та $h$

$y={\sqrt {1-r}}$

$h={\sqrt {r-r^{2}}}$

Радіус кола з центром O :

${\frac {1}{2}}{\sqrt {r-r^{2}}}.$

Тоді, площа :

$S_{circle}=\pi \left({\frac {1}{2}}{\sqrt {r-r^{2}}}\right)^{2}$

$S_{circle}={\frac {\pi r}{4}}-{\frac {\pi r^{2}}{4}}$

Площа арбелосу дорівнює різниці площ великого півкола та двох невеликих напівкіл. Тому площа арбелосу :

$S={\frac {\pi }{8}}-\left({\frac {\pi }{2}}\left({\frac {r}{2}}\right)^{2}+{\frac {\pi }{2}}\left({\frac {1-r}{2}}\right)^{2}\right)$

$S_{arbelos}={\frac {\pi -\pi r^{2}-\pi +2\pi r-\pi r^{2}}{8}}$

$S_{arbelos}={\frac {\pi r}{4}}-{\frac {\pi r^{2}}{4}}=A_{circle}$

Q.E.D.

Прямокутник

Скульптура арбелосу в Kaatsheuvel, Нідерланди

Хай $D$ та $E$ будуть точками, де відрізки $BH$ та $CH$ перетинають півкола $AB$ та $AC$, відповіно. Чотирикутник $ADHE$ є насправді прямокутником.

Доказ: Кути $BDA$, $BHC$, та $AEC$ є прямими, бо вони вписані до півкола (за теоремою Фалеса). Чотирикутник $ADHE$ тоді має три прямих кути, тож він є прямокутником.

Дотичні

Лінія $DE$ є дотичною до півкола $BA$ в точці $D$ та півкола $AC$ в $E$.

Доказ: Оскільки кут BDA є прямим, кут DBA дорівнює π/2 мінус кут DAB. Однак, кут DAH також дорівнює π/2 мінус кут DAB (оскільки кут HAB є прямим). Тоді трикутники DBA та DAH подібні. Тоді кут DIA подібний до кута DOH, де I є серединою BA та O є серединою AH. Але AOH є прямою, тож кути DOH та DOA є додатковими кутами. Тоді сума кутів DIA та DOA дорівнює π. Кут IAO прямий. Сума кутів будь-якого чотирикутника дорівнює 2π, тож у чотирикутнику IDOA, кут IDO повинен бути прямим. Але ADHE являє собою чотирикутник, тож середина AH (діагональ чотирикутника) крапка О також є серединою DE (іншої діагоналі). Тоді I (середина BA) є центром півкола BA, так кут IDE є прямим, тоді DE є дотичною до півкола BA в точці D. Аналогічно доводимо, що DE є дотичною до півкола AC в точці E.

Кола Архімеда

Висота $AH$ ділить арбелос на дві області, кожна з яких обмежена півколом, сегментом прямий і дугою зовнішнього півкола. Кола, вписані в кожну з цих областей, відомі як кола Архімеда цього арбелосу та мають однаковий розмір.

Теорема Паппа Александрійського

Теорема Паппа: $h_{1}=d_{1}$, $h_{2}=2d_{2}$,…, $h_{n}=nd_{n}$.

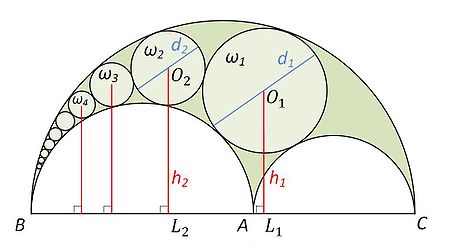
Маємо арбелос ABC (крапка A лежить між крапками B та C) та кола $\omega _{1}$, $\omega _{2}$,…,$\omega _{n}$ ($n\in N$), за умов, що коло $\omega _{1}$ дотикається до дуг AB, BC та AC, та коли $n\geqslant 2$ коло $\omega _{n}$ дотикається до дуг AB та BC та кола $\omega _{n-1}$. Тоді для кожного натурального $n$ відстань до центра кола $\omega _{n}$ до прямої BC дорівнює добутку діаметра цього кола та її номера $n$:

$h_{n}=nd_{n}$.

Див. також

• Ідеальний трикутник
• Томагавк (геометрія)

Бібліографія

• Джонсон Р. А. (1960). Розширена евклідова геометрія: Елементарний трактат з геометрії трикутника і кола (вид. перевиданий у 1929 в редагуванні Хоутона Міфліна). Нью Йорк: Dover Publications.
• Огілві, Ц. С. (1990). Екскурсіі по геометрії. Dover Publications.
• Сондоу, Дж. (2012). Параболос, параболичний аналог арбелосу.
• Уельс, Д. (1991). Словник пінгвіна з кумедної та цікавої геометрії. Нью Йорк: Penguin Books.