Теорема про відсутність безкоштовних сніданків у пошуку та оптимізації

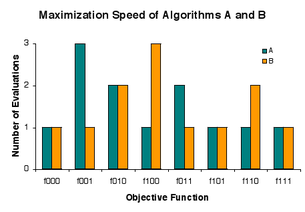
В обчислювальних процесах є обставини, за яких усі методи розв'язку однієї задачі виявляються статистично ідентичними. Мальовничим способом представлення таких обставин, запропонованим Девідом Вульпертом та Вільямом Дж. Маккріді в зв'язку з проблемами пошуку та оптимізації, є вислів — «Безкоштовних сніданків не існує». Перед цим Вульперт вивів цю теорему для машинного навчання (статистичного висновування). Перед публікацією роботи Вульперта, Каллен Шаффер підсумував переддруковану версію роботи Вульперта, але використав іншу термінологію.

В розгорненні метафори про безкоштовні сніданки, кожен «ресторан» (процедура, що розв'язує проблему) має «меню», асоціюючи кожну «страву» (проблему) з ціною (продуктивністю процедури, що вирішує цю проблему). Меню ресторанів ідентичні за винятком однієї деталі — ціни перемішані від одного ресторану до іншого. Для всеядної істоти, яка буде куштувати будь-яку страву, середня вартість обіду не залежить від вибору ресторану. Але вегетаріанець, що регулярно снідає разом з плотоядним та бажає заощадити, платить високу середню ціну за один сніданок. Для поступового зниження середньої вартості, потрібно мати поглиблені знання про a) власне саме замовлення та b) вартість цієї страви в усіх ресторанах. Таким чином, підвищення продуктивності розв'язання проблем потребує використання попередньої інформації для зіставлення процедур і проблем.

В формальному значенні, вільних сніданків не існує коли ймовірнісний розподіл випадків проблеми такий, що всі розв'язувані проблеми мають однаково розподілені результати. У випадку пошуку, кожен екземпляр проблеми є цільовою функцією, а результатом — послідовність значень, отриманих оцінкою допустимих розв'язків в області значень функції. В типовій інтерпретації результатів, пошук — це процес оптимізації. Безкоштовних сніданків у пошуку немає у випадку, коли і тільки коли розподіл цільової функції є константою з перестановок на множині допустимих розв'язків. Ця умова не виконується точно на практиці, але теорема про (майже) не існуючі безкоштовні сніданки пропонує її наближене виконання.

Загальні відомості

Деякі обчислювальні задачі розв'язуються пошуком гарних розв'язків у множині допустимих розв'язків. Опис того, як швидко знаходити гарні розв'язки та відкидати погані, називається пошуковим алгоритмом. На конкретній проблемі різні алгоритми можуть показувати різні результати, але на множині всіх задач вони нерозрізнювані. Це розповсюджується на властивість алгоритмів платити за першість у розв'язку одних задач значно гіршими результатами на інших задачах. В такому сенсі, у пошуку немає безкоштовних сніданків. З іншого боку, згідно з Шаффером, продуктивність пошуку зберігається. Зазвичай пошук інтерпретується як оптимізація, і це веде до спостереження, що безкоштовних сніданків немає також в оптимізації.

«Теорема про відсутність безкоштовних сніданків Вульперта та Маккріді», як дослівно зазначено самими Вульпертом і Маккріді, полягає в тому, що «продуктивність будь-яких двох алгоритмів у середньому однакова при розв'язанні всіх можливих задач». Наслідки відсутності безкоштовного сніданку свідчать про те, що підбір специфічного алгоритму для кожної проблеми дає в середньому кращі результати, ніж застосування одного й того самого алгоритму до всієї множини задач. Айгель, Туссон та Інглиш уклали спільну угодну про відсутність безкоштовного сніданку взагалі. Вважаючи, що фізично це можливо, теорема не завжди виконується точно. Дросте, Джансес та Вегенер довели теорему, яку вони інтерпретують як «Безкоштовних сніданків (майже) не існує», на практиці.

Для конкретизації суті можна розглянути оптимізатора-виконавця, якому була поставлена задача. Маючи деяку інформацію про виникнення цієї проблеми, оптимізатор може використовувати ці знання для вибору достатньо продуктивного алгоритму для розв'язання задачі. Якщо виконавець не може застосувати ці знання при виборі алгоритму, або взагалі не має таких знань, перед ним постає питання, чи існують алгоритми, які загалом показують найкращі результати при розв'язанні реальних задач. Автори теореми про (майже) відсутність безкоштовних сніданків дають негативну по суті відповідь на це питання, але залишають місце для деяких резервацій, зважаючи на те, наскільки теорема застосована до виконавця.

Відсутність безкоштовних сніданків (NFL)

Більш формально, задача — цільова функція, що співставляє допустимий розв'язок з деякою якісною оцінкою. Алгоритм пошуку приймає на вхід цільову функцію та один по одному обчислює допустимі розв'язки. Результатом роботи алгоритму є послідовність знайдених якісних оцінок.

Вульперт та Маккріді обумовили, що алгоритм ніколи не переоцінює допустимий розв'язок, і продуктивність алгоритму оцінюється за кількістю знайдених розв'язків. Для спрощення можна знехтувати випадковістю в алгоритмах. За цих умов пошуковий алгоритм, виконуючись на кожному з можливих наборів вхідних даних, генерує кожний можливий вивід точно один раз. Оскільки швидкодія вимірюється за кількістю виводів, неможливо розрізнити, який з алгоритмів досягне вищих рівнів продуктивності.

Деякі методи вимірювання продуктивності показують, наскільки добре алгоритми пошуку оптимізують цільову функцію. Звісно, застосування алгоритмів пошуку до задач оптимізації виявляється набагато цікавішим. Найпоширенішою мірою швидкодії є найменший індекс найменшого значення у послідовності виводу. Це є кількістю обчислень, необхідною для мінімізації цільової функції. Для деяких алгоритмів час, що витрачається на пошук мінімуму, пропорційний кількості обчислень.

Оригінальна теорема про відсутність безкоштовних сніданків припускає, що всі цільові функції мають однаковий шанс потрапити на вхід пошукових алгоритмів. Пізніше було виявлено, що теорема може застосовуватися тоді і тільки тоді, коли «перемішування» цільових функцій не впливає на їхні ймовірності. Попри те, що ця умова дійсно можлива, було доведено що вона не виконується точно. Очевидна інтерпретація «не відсутності безкоштовних сніданків» — це «безкоштовні сніданки», але це не вірно. Теорема оперує ступенями, а не полярними поняттями «все або нічого». Якщо всі умови теореми виконуються наближено, то всі алгоритми маюсь приблизно однакові результати на всіх цільових функціях. Варто також зазначити, що «не відсутність безкоштовних сніданків» означає тільки що алгоритми не збігаються за деякими мірами продуктивності. Для заданої міри алгоритми можуть залишатися еквівалентними або наближеними.

Теоретично, всі алгоритми показують добрі результати у процесах оптимізації майже завжди. Тобто, алгоритм отримує добрі розв'язки за відносно невелике число обчислень на майже всіх цільових функціях. Причиною є те, що багато цільових функцій виявляють великий ступінь Колмогоровської складності. Це призводить до надзвичайної непостійності та непередбачуваності. Всі ступені якості рівномірно розподілені між допустимими розв'язками, та добрі розв'язки розкидані по всій множині допустимих розв'язків. Пошуковому алгоритму рідко доведеться перебрати велику кількість розв'язків, щоб знайти перший дійсно хороший. На практиці, майже всі цільові функції — алгоритми такої Колмогоровської складності, що вони не можуть виникати самі по собі. Типова цільова функція або алгоритм несуть в собі більше інформації, ніж всесвіт спроможний зареєструвати, згідно з Сетом Ллойдом. Наприклад, якщо кожен допустимий розв'язок закодовано послідовністю з 300 нулів та одиниць, та можливі ступені оцінки — 0 і 1, то більшість цільових функцій матимуть Колмогорівську складність 2300 біт, що більше за Ллойдівську межу 1090 ≈ 2299 біт. З цього випливає, що не всі теорії відсутності безкоштовного сніданку застосовані до фізичної реальності. В практичному сенсі, алгоритми, достатньо малі для застосування у фізичному світі, перевершують за швидкодією занадто великі.

Формальний синопсис NFL

$Y^{X}$ — набір всіх цільових функцій f:X→Y, де $X$ — скінчена множина розв'язків та $Y$ скінчена частково впорядкована множина. Набором всіх можливих перестановок з X є J. Випадкова величина F розподілена на $Y^{X}$ . Для всіх j з J, F o j — випадкова величина, розподілена на $Y^{X}$ , з ймовірністю P(F o j = f) = P(F = f o j⁻¹) для всіх f з $Y^{X}$ .

Нехай a(f) позначає вивід алгоритму пошуку a на вхід f. Якщо a(F) та b(F) однаково розподілені для всіх пошукових алгоритмів a та b, тоді F має NFL розподілення. (NFL від No Free Lunch — «не існує безкоштовних сніданків»). Ця умова виконується тоді і тільки тоді, коли F та F o j однаково розподілені для всіх j з J. Іншими словами, для алгоритмів не існує безкоштовних сніданків тоді і тільки тоді, коли розподілення цільових функцій є постійною величиною від перестановок множини розв'язків.

Частина «тільки тоді» була вперше опублікована С Шумахером в його докторській дисертації «Пошук чорного ящика — фреймворки та методи» (Универсітет Тенессі, Ноксвілль (2000)). Теоретичні NFL теореми нещодавно були узагальнені для довільного відношення

Початкова NFL-теорема

Вульперт та Маккріді представили дві принципові теореми про відсутність безкоштовних сніданків — для цільових функцій, що не можуть змінюватися під час пошуку та для тих, що можуть. Теорема 1: Для будь-якої пари алгоритмів a1 та a2 Це означає, що коли всі функції f однаково можливі, ймовірність спостереження деякої послідовності з m значень під час пошуку не залежить від алгоритму пошуку. Теорема 2 встановлює «більш суттєвий» NFL-результат для цільових функцій, що змінюються в часі.

Інтерпретація наслідків NFL

Зручний, але не дуже точний підхід до інтерпретації наслідків теореми полягає в тому, що «універсальна глобальна оптимізація теоретично неможлива, і єдиний шлях для однієї стратегії бути продуктивніше за іншу — це бути спеціально налаштованою для розв'язання певного класу задач». Декілька коментарів щодо цього:

Універсальний майже загальний оптимізатор теоретично можливий. Будь-який алгоритм пошуку виявляє добрі результати майже на всіх цільових функціях.

Алгоритм може перевершити інший у випадку, коли жоден з них не спеціалізується на задачі. Можливий варіант, коли обидва алгоритми найгірші для розв'язання проблеми. Вульперт та Маккріді розробили систему оцінки «збігу» між алгоритмом та задачею. Сказати, що один алгоритм кращий за інший у розв'язанні задачі — це не обов'язково має на увазі, що один з алгоритмів спеціалізується на цій задачі.

На практиці, деякі алгоритми переоцінюють допустимі розв'язки. Перевага алгоритму, що ніколи не переоцінює розв'язки, над тим, що переоцінює, не обов'язково означає спеціалізацію одного з алгоритмів на проблемі.

Для майже всіх цільових функцій, спеціалізація цілком випадкова. Через Колмогорівську складність, цільові функції не мають постійності, яку міг би використати алгоритм. Маючи нестисливу цільову функцію, нема підстав для вибору певного алгоритму. Якщо обраний алгоритм більшість часу показує добру продуктивність — це просто збіг.

На практиці, тільки значно стисні (далекі від випадковості) функції вміщуються в пам'ять комп'ютера, і немає випадку, коли один алгоритм видає добрі результати на всіх цільових функціях. Є загальна перевага у закладанні знань про проблему в логіку алгоритму. В той час, коли результати NFL встановлюють, у звуженому сенсі, теореми повної зайнятості для професіоналів в оптимізації, важливо не приймати цей термін буквально. По-перше, люди зазвичай мають недостатньо знань для роботи. По-друге, привнесення початкових знань не дає значної переваги для деяких задач. Нарешті, людський час значно дорожче комп'ютерного часу. Існує багато випадків, коли компанія обирає повільну оптимізацію за допомогою цілком комп'ютерної програми, а не швидку оптимізацію, яка залучає людей. Наслідки NFL не означають, що не варто здійснювати «постріли всліпу» при розв'язку задач з неспеціалізованими алгоритмами. Ніхто не виявив долю задач, в якій алгоритм зможе знайти гарний розв'язок швидко. Також існує практично безкоштовний сніданок, що не конфліктує с загальною теорією. Виконання реалізації алгоритму на комп'ютері значно дешевше людської праці, навіть заради гарного розв'язку. Якщо алгоритм здатен знайти задовільний розв'язок за прийнятний проміжок часу — маленький вклад приніс значний прибуток. Якщо ж розв'язок не знайдено — понесені втрати незначні.

Коеволюційні безкоштовні сніданки

Вульперт та Маккріді довели, що безкоштовні сніданки існують в коеволюційній оптимізації. Їхній аналіз покриває задачі «самогри». В цих задачах, група гравців працює разом заради створення чемпіона, який потім перемагає супротивників в грі між декількома гравцями". Тобто, ціллю є отримання гарного гравця, але без цільової функції. Якість кожного гравця (допустимого розв'язку) визначається за тим, як добре він грає супроти інших гравців. Алгоритм використовує гравців та їхні властивості для отримання кращих гравців. Гравець, обраний алгоритмом з-поміж інших, є чемпіоном. Вульперт і Маккріді продемонстрували загальну перевагу коеволюційних алгоритмів над іншими за якістю отриманих чемпіонів. Створення чемпіона за допомогою самогри є питанням еволюційних обчислень та теорії ігор. Результати неможливо застосувати до еволюції біологічних видів, оскільки вони не мають чемпіонів.

Див. також

Посилання

http://www.no-free-lunch.org [Архівовано 12 лютого 2022 у Wayback Machine.]
Yin-Yang: No-Free-Lunch Theorems for Search
Radcliffe and Surry, 1995, «Fundamental Limitations on Search Algorithms: Evolutionary Computing in Perspective» (the first published paper on NFL, available in various formats) [Архівовано 14 січня 2006 у Wayback Machine.]
NFL publications by Thomas English [Архівовано 5 березня 2016 у Wayback Machine.]
NFL publications by Christian Igel and Marc Toussaint [Архівовано 23 квітня 2007 у Wayback Machine.]
NFL and «free lunch» publications by Darrell Whitley [Архівовано 8 лютого 2012 у Wayback Machine.]
Publications by David Wolpert, William Macready, and Mario Koeppen on optimization and search [Архівовано 8 березня 2012 у Wayback Machine.]