Розподіл ймовірностей

Дискретний розподіл ймовірностей для суми двох гральних кісток

В математиці та статистиці, розпо́діл імові́рностей (який має математично описуватися функцією розподілу ймовірностей), ставить у відповідність кожному інтервалу ймовірність таким чином, що аксіоми ймовірностей виконуються. Математичною мовою, функція розподілу ймовірностей є ймовірнісною мірою, визначеною на борелівській алгебрі інтервалів.

Розподіл імовірностей є окремим випадком загальнішого означення ймовірнісної міри, яка є функцією, що ставить у відповідність вимірним множинам з вимірного простору ймовірності за аксіомами Колмогорова.

Згідно з означенням П. Лапласа, мірою ймовірності є дріб, чисельником якого є число сприятливих подій, а знаменником — число всіх можливих випадків.

Також, деякі вчені означають розподіл як ймовірнісну міру, індуковану випадковою величиною X на деякому інтервалі — ймовірність множини B є $P(X^{-1}(B))$. Однак, у цій статті розглядаємо лише ймовірнісні міри на множині інтервалів числової прямої.

Строге визначення

Будь-яка випадкова величина задається своїм розподілом імовірностей. Якщо X є випадковою величиною, його розподіл ставить у відповідність відрізкам [a, b] ймовірність Pr[a ≤ X ≤ b], тобто ймовірність, що випадкова величина X прийме значення з інтервалу [a, b]. Розподіл ймовірностей величини X може бути однозначно описаний своєю функцією розподілу ймовірностей F(x), яка визначається, як

$F(x) = \Pr\left[ X \le x \right]$

для усіх x з R.

Розподіл є дискретним, якщо його функція розподілу складається зі скінченної послідовності уступів, що фактично означає, що величина X є дискретною випадковою величиною: вона може набувати значення лише із визначеної скінченної (або зліченної) множини. Дехто визначає неперервний розподіл як такий, що його функція розподілу є неперервною функцією, що означає, що вона відповідає такій випадковій величині X для якої Pr[ X = x ] = 0 для усіх x в R. Інше визначення використовує термін неперервна функція розподілу лише для абсолютно неперервного розподілу. В термінах функції щільності, на множині дійсних чисел визначено невід'ємний інтеграл Лебега функції fщо задовольняє умові

$\Pr \left[ a \le X \le b \right] = \int_a^b f(x)\,dx$

для всіх a та b. Очевидно, для дискретних розподілів функція щільності не визначена; хоча треба відмітити, що для деяких неперервних розподілів, як драбина Кантора функція щільності також не визначена.

Дискретна функція розподілу виражається як -

$F(x) = \Pr \left[X \le x \right] = \sum_{x_i \le x} p(x_i)$

для $i = 1, 2, ...\,\!$.

Де $p(x_i)\,\!$ є ймовірністю елементарної події.

• Розподіл імовірностей суми двох незалежних випадкових величин є згорткою їх функцій щільності.
• Розподіл імовірностей різниці двох незалежних випадкових величин є крос-кореляцією їх функцій щільності.

Список важливих ймовірнісних розподілів

Деякі ймовірнісні розподіли є дуже важливим в теорії та практиці, тож їм дали свої назви:

Дискретні розподіли

Зі скінченною множиною подій

• Розподіл Бернуллі, що приймає значення 1 з ймовірністю p і значення 0 з ймовірністю q = 1 − p.
• Розподіл Радемахера (англ. Rademacher distribution), що приймає значення 1 з імовірністю 1/2 та значення −1 з імовірністю 1/2.
• Біноміальний розподіл описує кількість успіхів в схемі незалежних випробувань Бернуллі.
• Вироджений розподіл в x₀, де X приймає значення x₀ завжди. На перший погляд, такий розподіл не виглядає ймовірнісним, але він задовольняє означенню випадкової величини. Це часто стає в нагоді, оскільки вкладає однаковий зміст у константи і випадкові величини.
• Дискретний рівномірний розподіл, де всі елементи скінченної множини є рівноймовірними. Вважають, що це розподіл симетричної монети, «правильного» кубика, рулетки в казино чи добре перетасованої колоди карт. Також для генерації рівномірно розподілених випадкових величин можна використовувати міри квантових станів (measurements of quantum states). Все це «фізичні» чи «механічні» прилади, що можуть зазнати помилок в будові чи впливу довкілля, тож рівномірний розподіл є тільки наближенням до їх поведінки. У цифрових комп'ютерах для створення статистично випадкового дискретного рівномірного розподілу використовують псевдовипадкові генератори випадкових чисел.
• Гіпергеометричний розподіл, що описує кількість успіхів у перших m із ряду з n незалежних стохастичних дослідів виду Так/Ні у випадку коли відоме загальне число успіхів.
• Розподіл Зіпфа. Дискретний степеневий розподіл, чиїм найвідомішим прикладом є опис частоти слів у англійській мові.
• Розподіл Зіпфа-Мандельброта, який є узагальненим розподілом Зіпфа.

З нескінченою множиною подій

• Розподіл Больцмана, дискретний розподіл, застосовується в статистичній фізиці, що описує ймовірності різних дискретних рівнів системи в термодинамічній рівновазі. Має неперервний аналог. До спеціальних видів належать:
  • Розподіл Гіббса
  • Розподіл Максвелла-Больцмана
  • Розподіл Бозе-Ейнштейна
  • Розподіл Фермі-Дірака
• Геометричний розподіл, дискретний розподіл, що описує кількість спроб необхідних щоб отримати перший успіх в схемі незалежних випробувань Бернуллі.

Пуассонівський розподіл

• логарифмічний (ряд) розподіл
• Від'ємний біноміальний розподіл, узагальнення геометричного розподілу до nго успіху.
• parabolic fractal distribution
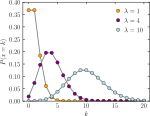
• Пуассонівський розподіл, що описує велику кількість малоймовірних подій протягом деякого інтервалу часу.

Розподіл Skellam

• Розподіл Скелама, розподіл різниці двох незалежних пуассонівських випадкових величин.
• Розподіл Юле-Саймона (англ. Yule-Simon distribution)
• Зета-розподіл застосовується в прикладній статистиці та статистичній механиці, та може становити інтерес в теорії чисел. Є розподілом Зіпфа для нескінченної кількості елементів.

Неперервні розподіли

Визначені на замкненому інтервалі

Бета розподіл

Рівномірний розподіл (неперервний)

• Бета розподіл на [0,1], частковим випадком якого є рівномірний розподіл, використовується для оцінки ймовірностей успіху.
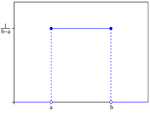
• Неперервний рівномірний розподіл на [a,b], має однакове значення в усіх точках інтервалу.
  • Прямокутний розподіл рівномірний розподіл на [-1/2,1/2].
• Дельта функція Дірака не будучи функцією, є граничною формою багатьох неперервних функцій розподілу. Представляє дискретний розподіл зосереджений поблизу від 0 — вироджений розподіл — але він позначається так, наче є неперервним.
• Розподіл Кумарасвамі (англ. Kumaraswamy distribution) настільки ж гнучкий як і Бета розподіл, але має простий замкнений вигляд для cdf та pdf.
• Логарифмічний розподіл (неперервний)
• Трикутний розподіл на інтервалі [a, b], окремим випадком якого є сума двох рівномірно розподілених величин (згортка двох рівномірних розподілів).
• Розподіл фон Майсеса на колі.
• Розподіл фон Майсеса-Фішера — на N-вимірній сфері включає розподіл фон Майсеса в якості окремого випадку.
• Розподіл Кента на тривимірній сфері.
• Розподіл Віґнера на напівколі відіграє важливу роль в теорії випадкових матриць.

Визначений на пів-інтервалі [0,∞)

Розподіл хі-квадрат

Експоненціальний розподіл

Гамма-розподіл

Розподіл Парето

• Хі-розподіл
• Нецентрований хі-розподіл
• Розподіл хі-квадрат, що є сумою квадратів n незалежних Гаусівських випадкових величин. Це частковий випадок Гамма-розподілу.
  • Обернений розподіл хі-квадрат
  • Нецентрований розподіл хі-квадрат
  • Масштабований обернений розподіл хі-квадрат
• Експоненціальний розподіл, що описує час між двома послідовними рідкими випадковими подіями під час процесу без післядії.
• F-розподіл, що є розподілом частки двох (нормалізованих) хі-квадрат-розподілених випадкових величин. Його використовують в аналізі дисперсії (англ. analysis of variance). (Коли частка двох хі-квадрат-розподілених величн не нормалізована діленням їх на кількість ступенів свободи, цей розподіл ще називають Бета розподіл другого роду.)
  • Нецентрований F-розподіл
• Гама-розподіл, що описує час, за який n послідовних рідких подій відбудуться в процесі без післядії.
  • Розподіл Ерланга, що є частковим випадком гамма розподілу, і застосовується для визначення часу очікування в системах масового обслуговування.
  • Обернений гамма-розподіл
• Напів-нормальний розподіл
• Розподіл Леві
• Лог-логістичний розподіл
• Логнормальний розподіл, що описує змінні, які можуть бути змодельовані як добуток багатьох малих незалежних додатніх випадкових величин.
• Розподіл Парето, або розподіл «за степеневим законом», що його використовують в аналізі фінансових даних та критичної поведінки (critical behavior).
• Розподіл Пірсона тип ІІІ (див розподіли Пірсона)
• Розподіл Рейлі
• Розподіл Райса
• Розподіл Ґамбела типу 2
• Розподіл Вальда
• Розподіл Вейбулла, чиїм частинним випадком є експоненціальний розподіл, використовують аби змоделювати життевий цикл технічних приладів.

Визначені на всій дійсній осі

Розподіл Коші

Розподіл Лапласа

Розподіл Леві

Нормальний розподіл

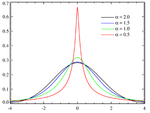
• Розподіл Коші, є прикладом розподілу, для якого не існує математичного сподівання, дисперсії та інших моментів. У фізиці він зазвичай називається функцією Лоренца, і пов'язаний з багатьма процесами, включаючи розподіл енергетичного резонансу, натуральне та вимушене розширення спектральних ліній.
• z-розподіл Фішера
• гіперболічний розподіл
• Розподіл Ландау
• Розподіл Лапласа
• Нормальний розподіл, також називається Гаусівським, або дзвоном. Розповсюджений в природі та статистиці завдяки центральній граничній теоремі: кожна випадкова величина, яка може бути змодельована як сума великої кількості незалежних випадкових величин є майже нормально розподіленою.
• Розподіл Пірсона IV типу (див. Розподіли Пірсона)
• t-розподіл Стьюдента
  • нецентрований t-розподіл

Згортка розподілів

Для будь-якої множини незалежних випадкових величин функція щільності їх загального розподілу є добутком їх функцій щільності.

Ймовірносний простір розмірності більше 1

• Розподіл Діріхле, узагальнення бета розподілу.
• поліноміальний розподіл, узагальнення біноміального розподілу.
• Багатовимірний нормальний розподіл, узагальнення нормального розподілу.

Матричні розподіли

• нормальний матричний розподіл
• матричний t-розподіл

Приклади розподілів

• Розподіл Кантора
• Truncated distribution

Дивиться також

• функція щільності
• випадкова величина
• гістограма

Посилання

• Інтерактивні дискретні та неперервні ймовірносні розподіли
• Збірка основних ймовірносних розподілів
• Статистичні розподіли - Огляд
• Ймовірносні розподіли
• Статистика - Розподіли