Логарифмічна амплітудно-частотна характеристика

ЛАФЧХ фільтра Баттерворта першого порядка

Логарифмічна амплітудно-фазова частотна характеристика (ЛАФЧХ) — представлення частотного відгуку лінійної стаціонарної системи в логарифмічному масштабі.

Загальна характеристика

ЛАФЧХ будується у вигляді двох графіків: логарифмічної амплітудно-частотної характеристики і фазо-частотної характеристики, які зазвичай розташовуються один під одним.

Аналіз систем за допомогою ЛАФЧХ дуже простий і зручний, тому знаходить широке застосування в різних галузях техніки, таких як цифрова обробка сигналів, електротехніка та теорія управління.

ЛАЧХ

ЛАЧХ — це залежність модуля коефіцієнта посилення ($20\cdot log\left({\frac {|Vout|}{|Vin|}}\right)$ для напруги або струму, та $10\cdot log\left({\frac {|Pout|}{|Pin|}}\right)$ для потужності), від частоти в логарифмічному масштабі.

Масштаб за віссю абсцис ЛАЧХ

За віссю абсцис відкладається частота в логарифмічному масштабі, одиниця вимірювання — безрозмірна величина: декада (дек): 1 декада дорівнює зміні частоти в 10 разів.

октава (окт): 1 октава дорівнює зміні частоти в 2 рази.

Масштаб за віссю ординат ЛАЧХ

За віссю ординат відкладається амплітуда вихідного сигналу в логарифмічних безрозмірних величинах: децибел (дБ) (десята частина бела) — це відношення потужностей (10 децибел дорівнює зміні потужності в 10 разів).

1 децибел дорівнює (для амплітуд розмірності напруги) одній двадцятій зміни амплітуди сигналів в 10 разів.

Непер (Нп): 1 Непер дорівнює зміні амплітуди сигналів в е раз

ЛФЧХ

ЛФЧХ — це залежність фази вихідного сигналу від частоти в напівлогарифмічному масштабі

За віссю абсцис відкладається частота в логарифмічному масштабі (в декадах або октавах)

За віссю ординат відкладається вихідна фаза в кутових градусах або радіанах.

Непер і октави в даний час є застарілими і практично не використовуються.

Причини побудови амплітудних і фазних характеристик в логарифмічному масштабі — можливість дослідження характеристик у великому діапазоні.

Асимптотичні ЛАЧХ і ЛФЧХ

Власне ЛАЧХ і ЛФЧХ мало використовуються на практиці.

Для більш наочного аналізу характеристик застосовуються їх модифіковані варіанти — асимптотична логарифмічна амплітудно-частотна характеристика (АЛАЧХ) і асимптотична логарифмічна фазо-частотна характеристика (АЛФЧХ), при цьому крива замінюється відрізками ламаної прямої. Зазвичай слово «асимптотична» опускають, але завжди треба пам'ятати, що АЛАЧХ (АЛФЧХ) і ЛАЧХ (ЛФЧХ) — це різні характеристики.

Аналіз систем за допомогою АЛФЧХ вельми простий і зручний, тому знаходить широке застосування в різних галузях техніки, таких, як цифрова обробка сигналів, електротехніка і теорія управління.

Назва

У західній літературі використовується назва діаграма Боде або графік Боде, на ім'я видатного інженера Хенріка Боде (англ. Hendrik Wade Bode).

В інженерних колах назва зазвичай скорочується до Лах.

У пакеті прикладних програм для інженерних обчислень GNU Octave і MATLAB для побудови ЛАФЧХ використовується функція bode.

Використання

Властивості і особливості

Якщо передавальна функція системи є раціональною, тоді АЛАЧХ може бути апроксимована прямими лініями. Це зручно при малюванні АЛАЧХ вручну, а також при складанні ЛАЧХ простих систем.

За допомогою ЛАЧХ та ЛФЧХ зручно проводити синтез систем управління, а також цифрових і аналогових фільтрів: відповідно до визначених критеріїв якості будується бажана ЛАЧХ, апроксимована за допомогою прямих ліній, яка потім розбивається на ЛАЧХ окремих елементарних ланок, з яких відновлюється передавальна функція системи (регулятора) або фільтра.

ЛАЧХ

На графіку ЛАЧХ абсцисою є частота в логарифмічному масштабі, по осі ординат відкладена амплітуда передавальної функції в децибелах.

Подання АЧХ в логарифмічному масштабі спрощує побудова характеристик складних систем, так як дозволяє замінити операцію множення АЧХ ланок складанням, що випливає з властивості логарифмh: ${\lg(a\cdot b)=\lg(a)+\lg(b)}.$

ФЧХ

На графіку фазо-частотної характеристики абсцисою є частота в логарифмічному масштабі, по осі ординат відкладений фазовий зсув вихідного сигналу системи щодо вхідного (зазвичай в градусах).

Також можливий варіант, коли по осі ординат відкладається фазовий зсув в логарифмічному масштабі, в цьому випадку характеристика буде називатися ЛФЧХ.

Випадок мінімально-фазових систем

Амлітуда і фаза системи рідко змінюються незалежно один від одного — при зміні амплітуди змінюється і фаза, і навпаки. Для мінімально-фазових систем ЛФЧХ і ЛАЧХ можуть бути однозначно визначені один з одного за допомогою перетворення Гільберта — Уорренгтона.

Побудова ЛАФЧХ

Основна ідея ґрунтується на наступному математичному правилі складання логарифмів. Якщо передавальну функцію можна представити у вигляді дробово-раціональної функції

$f(x)=A\prod (x-c_{n})^{a_{n}},$

то:

${\log(f(x))=\log(A)+\sum a_{n}log(x-c_{n})}$

Після розбиття передавальної функції на елементарні ланки можна побудувати ЛАФЧХ кожної окремої ланки, а результуючу ЛАФЧХ отримати простим додаванням.

Побудова асимптотичної ЛАЧХ (апроксимація ЛАЧХ прямими лініями)

При побудові ЛАЧХ для осі ординат зазвичай використовується масштаб ${20\cdot \log _{10}(X)}$, тобто значення АЧХ, рівне 100, перетворюється в 40 децибел шкали ЛАЧХ. Якщо передавальна функція має вигляд:

$H(s)=A\cdot \prod {\frac {(s-x_{n})^{a_{n}}}{(s-y_{n})^{b_{n}}}}$

де $s$ - комплексна змінна, яку можна пов'язати з частотою, використовуючи наступну формальну заміну: {\ displaystyle s = j \ omega \} {\ displaystyle s = j \ omega \}, {\ displaystyle \ x_ {n}} \ x_ {n} і {\ displaystyle \ y_ {n}} \ y_ {n} - константи, а {\ displaystyle \ H} \ H - передавальна функція. Тоді побудувати ЛАЧХ можна, використовуючи наступні правила:

в кожному {\ displaystyle \ s} \ s, де {\ displaystyle \ omega \ = x_ {n}} \ omega \ = x_ {n} (нуль), нахил лінії збільшується на {\ displaystyle (20 \ cdot a_ {n })} (20 \ cdot a_ {n}) дБ на декаду.

в кожному {\ displaystyle \ s} \ s, де {\ displaystyle \ omega \ = y_ {n}} \ omega \ = y_ {n} (полюс), нахил лінії зменшується на {\ displaystyle (20 \ cdot b_ {n })} (20 \ cdot b_ {n}) дБ на декаду.

Початкове значення графіка можна знайти простий підстановкою значення кругової частоти {\ displaystyle \ omega \} \ omega \ в передавальну функцію.

Початковий нахил графіка залежить від числа і порядку нулів і полюсів, які менше початкового значення частоти. Він може бути знайдений за допомогою перших двох правил.

У разі наявності комплексно-сполучених нулів або полюсів необхідно використовувати ланки другого порядку, {\ displaystyle x ^ {2} + ax + b} {\ displaystyle x ^ {2} + ax + b}, нахил змінюється в точці {\ displaystyle { \ sqrt {b}}} {\ sqrt {b}} відразу на {\ displaystyle (40 \ cdot a_ {n})} (40 \ cdot a_ {n}) дБ на декаду.

Коригування апроксимувати ЛАЧХ

Для коригування ЛАЧХ, апроксимувати прямими лініями, треба: в кожному нулі поставити крапку на {\ displaystyle 3 \ cdot a_ {n} \} 3 \ cdot a_ {n} \ дБ вище лінії ({\ displaystyle 6 \ cdot a_ {n} \} 6 \ cdot a_ {n} \ дБ для двох комплексно-сполучених нулів)

в кожному полюсі поставити крапку на {\ displaystyle 3 \ cdot a_ {n} \} 3 \ cdot a_ {n} \ дБ нижче лінії ({\ displaystyle 6 \ cdot a_ {n} \} 6 \ cdot a_ {n} \ дБ для двох комплексно-сполучених полюсів)

плавно з'єднати точки, використовуючи прямі лінії як асимптоти

Побудова асимптотичної ЛФЧХ (апроксимація)

Для побудови апроксимувати ФЧХ використовують запис передавальної функції в тому ж вигляді, що і для ЛАЧХ:

$H(s)=A\prod {\frac {(s-x_{n})^{a_{n}}}{(s-y_{n})^{b_{n}}}}$

Основний принцип побудови ФЧХ — накреслити окремі графіки для кожного полюса або нуля, потім служив їх. Точна крива фазо-частотної характеристики задається рівнянням:

{\ Displaystyle \ varphi = \ operatorname {arctg} ({\ frac {\ Im (H (j \ omega))} {\ Re (H (j \ omega))}})} \ varphi = \ operatorname {arctg} ({\ frac {\ Im (H (j \ omega))} {\ Re (H (j \ omega))}})

Для того, щоб намалювати ФЧХ для кожного полюса або нуля, використовують такі правила: якщо {\ displaystyle \ A} \ A позитивно, почати лінію (з нульовим нахилом) в 0 градусів, якщо {\ displaystyle \ A} \ A негативно, почати лінію (з нульовим нахилом) в 180 градусів,

для нуля зробити нахил лінії вгору на {\ displaystyle 45 \ cdot a_ {n}} 45 \ cdot a_ {n} ({\ displaystyle 90 \ cdot a_ {n}} 90 \ cdot a_ {n} для комплексно сполученого) градусів на декаду починаючи з {\ displaystyle \ omega = {\ frac {x_ {n}} {10}}} \ omega = {\ frac {x_ {n}} {10}},

для полюса нахилити лінію вниз на {\ displaystyle 45 \ cdot b_ {n}} 45 \ cdot b_ {n} ({\ displaystyle 90 \ cdot b_ {n}} 90 \ cdot b_ {n} для комплексно сполученого) градусів на декаду починаючи з {\ displaystyle \ omega = {\ frac {y_ {n}} {10}}} \ omega = {\ frac {y_ {n}} {10}},

обнулити нахил знову коли фаза зміниться на {\ displaystyle 90 \ cdot a_ {n}} 90 \ cdot a_ {n} градусів для простого нуля або полюса і на {\ displaystyle 180 \ cdot a_ {n}} 180 \ cdot a_ {n } градусів для комплексно-сполученого нуля або полюса,

скласти всі лінії і намалювати результуючу.

ЛАФЧХ деяких типових елементарних ланок

Нижче представлена ​​таблиця, в яку поміщені передавальні функції і ЛАФЧХ деяких типових елементарних ланок. Велика частина лінійних стаціонарних систем може бути представлена ​​у вигляді з'єднання таких ланок. У таблиці $\ s$ — комплексна змінна.

№	Ланка	Передавальна функція	ЛАФЧХ	Примітки
1	пропорційна	$\ K$		$\ K=100$
2	ідеальна інтегрирувальна	$\ 1/s$
3	ідеальна диференціювальна	$\ s$
4	аперіодична	${\frac {1}{Ts+1}}$		$\ T=0,01$
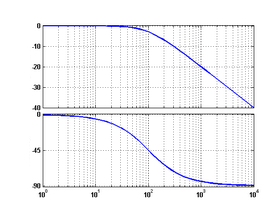5	коливальна	${\frac {1}{T^{2}s^{2}+2\;\xi \ Ts+1}}$		$\ T=0,01$ $\xi \ =0.1$
6	нестійка аперіодична (2-го порядку)	${\frac {1}{Ts-1}}$		$\ T=0,01$ немінімально-фазова
7	диференціювальна першого порядку	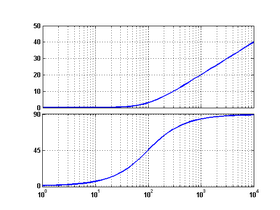$\ Ts+1$		$\ T=0,01$
8	форсувальна второго порядка	$\ T^{2}s^{2}+2\;\xi \ Ts+1$		$\ T=0,01$ $\xi \ =0.1$
9	чистого запізнювання	$\ e^{-sT}$		$\ T=0.0001$

Обґрунтування

В основі визначення стійкості системи розглядається модель у вигляді ланки, охопленого негативним зворотним зв'язком і можливість її входження в автоколебания (коливальна межа стійкості). Умовою автоколебаний є наявність позитивного зворотного зв'язку при цьому коефіцієнт посилення в прямій ланцюга повинен бути не нижче одиниці. Фаза вихідного сигналу (описувана фазо-частотної характеристикою) через ланцюг негативного зворотного зв'язку подається назад на вхід, при цьому «запасом по фазі» називається додатковий зсув по фазі, який повинен бути на виході, щоб вийшла позитивний зворотний зв'язок. Коефіцієнт передачі в прямий галузі описується амплітудно-частотної характеристикою, при цьому частота, якій відповідає одиничне посилення називається «частотою зрізу», на ЛАЧХ частота зрізу-це точка перетину характеристики з віссю абсцис. Графічно запас по фазі визначається як різниця між фазою рівною π радіан (180 °) і фазою на частоті зрізу (умова освіти позитивного зворотного зв'язку); «Запас по амплітуді» — відстань по осі амплітуд від точки частоти зрізу до амплітуди при вугіллі π радіан (умова одиничного коефіцієнта в прямої гілки).

Алгоритм обчислення

Для визначення стійкості замкнутої системи будується ЛАФЧХ розімкнутої системи (див. Рис.). Після цього необхідно знайти частоту зрізу ωср, вирішивши рівняння {\ displaystyle A (\ omega _ {cp}) = 0} A (\ omega _ {cp}) = 0 (тут і далі {\ displaystyle A (\ omega) = 20 \ lg | W (j \ omega) |} A (\ omega) = 20 \ lg | W (j \ omega) |; якщо коренів декілька, необхідно вибрати найбільший корінь), і частоту ωв - максимальну з частот, для яких { \ displaystyle \ varphi (\ omega) = - 180 ^ {\ circ}} \ varphi (\ omega) = - 180 ^ {\ circ}. Тоді {\ displaystyle \ Delta A = A (\ omega _ {B})} \ Delta A = A (\ omega _ {B}) - запас стійкості по амплітуді, {\ displaystyle \ Delta \ varphi = \ varphi (\ omega _ {cp}) + 180 ^ {\ circ}} \ Delta \ varphi = \ varphi (\ omega _ {cp}) + 180 ^ {\ circ} - запас стійкості по фазі. Якщо ці запаси негативні, то замкнута система нестійка; якщо дорівнюють нулю - знаходиться на межі стійкості.

Див. також

• АФЧХ
• Передавальна функція
• ФЧХ
• Діаграма Сміта

Література

• Іванов А. О. Теорія автоматичного керування: Підручник. — Дніпропетровськ: Національний гірничий університет. — 2003. — 250 с.
• Енциклопедія кібернетики. тт. 1, 2. — К.: Головна редакція УРЕ, 1973. — 584 с.